Динамическая система — Википедия

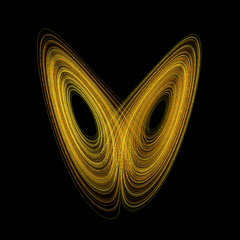
Динамическая система — множество элементов, для которого задана функциональная зависимость между временем и положением в фазовом пространстве каждого элемента системы.^{[источник не указан 2515 дней]} Данная математическая абстракция позволяет изучать и описывать эволюцию систем во времени.

Состояние динамической системы в любой момент времени описывается множеством вещественных чисел (или векторов), соответствующим определённой точке в пространстве состояний. Эволюция динамической системы определяется детерминированной функцией, то есть через заданный интервал времени система примет конкретное состояние, зависящее от текущего.

Введение[править | править код]

Динамическая система представляет собой такую математическую модель некоего объекта, процесса или явления, в которой пренебрегают «флуктуациями и всеми другими статистическими явлениями».^[1]

Динамическая система также может быть представлена как система, обладающая состоянием. При таком подходе, динамическая система описывает (в целом) динамику некоторого процесса, а именно: процесс перехода системы из одного состояния в другое. Фазовое пространство системы — совокупность всех допустимых состояний динамической системы. Таким образом, динамическая система характеризуется своим начальным состоянием и законом, по которому система переходит из начального состояния в другое.

Различают системы с дискретным временем и системы с непрерывным временем.

В системах с дискретным временем, которые традиционно называются каскадами, поведение системы (или, что то же самое, траектория системы в фазовом пространстве) описывается последовательностью состояний. В системах с непрерывным временем, которые традиционно называются потоками, состояние системы определено для каждого момента времени на вещественной или комплексной оси. Каскады и потоки являются основным предметом рассмотрения в символической и топологической динамике.

Динамическая система (как с дискретным, так и с непрерывным временем) часто описывается автономной системой дифференциальных уравнений, заданной в некоторой области и удовлетворяющей там условиям теоремы существования и единственности решения дифференциального уравнения. Положениям равновесия динамической системы соответствуют особые точки дифференциального уравнения, а замкнутые фазовые кривые — его периодическим решениям.

Основное содержание теории динамических систем — это исследование кривых, определяемых дифференциальными уравнениями. Сюда входит разбиение фазового пространства на траектории и исследование предельного поведения этих траекторий: поиск и классификация положений равновесия, выделение притягивающих (аттракторы) и отталкивающих (репеллеры) множеств (многообразий). Важнейшие понятия теории динамических систем — устойчивость состояний равновесия (то есть способность системы при малых изменениях начальных условий сколь угодно долго оставаться около положения равновесия или на заданном многообразии) и грубость (то есть сохранение свойств при малых изменениях самой математической модели; «грубая система — это такая, качественный характер движений которой не меняется при достаточно малом изменении параметров»).^[2][1]

Привлечение вероятностно-статистических представлений в эргодической теории динамических систем приводит к понятию динамической системы с инвариантной мерой.

Современная теория динамических систем является собирательным названием для исследований, где широко используются и эффективным образом сочетаются методы из различных разделов математики: топологии и алгебры, алгебраической геометрии и теории меры, теории дифференциальных форм, теории особенностей и катастроф.

Методы теории динамических систем востребованы в других разделах естествознания, таких как неравновесная термодинамика, теория динамического хаоса, синергетика.

Определение[править | править код]

Пусть ${\displaystyle X}$ — произвольное гладкое многообразие.

Динамической системой, заданной на гладком многообразии ${\displaystyle X}$, называется отображение ${\displaystyle g\colon \mathbb {R} \times X\to X}$, записываемое в параметрическом виде ${\displaystyle g^{t}(x)}$, где ${\displaystyle t\in \mathbb {R} ,x\in X}$, которое является дифференцируемым отображением, причём ${\displaystyle g^{0}}$ — тождественное отображение пространства ${\displaystyle X}$. В случае стационарных обратимых систем однопараметрическое семейство ${\displaystyle \{g^{t}:t\in \mathbb {R} \}}$ образует группу преобразований топологического пространства ${\displaystyle X}$, а значит, в частности, для любых ${\displaystyle t_{1},t_{2}\in \mathbb {R} }$ выполняется тождество ${\displaystyle g^{t_{1}}\circ g^{t_{2}}=g^{t_{1}+t_{2}}}$.

Из дифференцируемости отображения ${\displaystyle g}$ следует, что функция ${\displaystyle g^{t}(x_{0})}$ является дифференцируемой функцией времени, её график расположен в расширенном фазовом пространстве ${\displaystyle \mathbb {R} \times X}$ и называется интегральной траекторией (кривой) динамической системы. Его проекция на пространство ${\displaystyle X}$, которое носит название фазового пространства, называется фазовой траекторией (кривой) динамической системы^{[источник?]}.

Задание стационарной динамической системы эквивалентно разбиению фазового пространства на фазовые траектории. Задание динамической системы в общем случае эквивалентно разбиению расширенного фазового пространства на интегральные траектории^{[источник?]}.

Замена координат представляет собой диффеоморфизм (если структура гладкая) или гомеоморфизм (с топологической точки зрения) фазовых пространств. Можно определить множество эквивалентности между динамическими системами, которые связаны с разными классами координат. Проблема структуры орбит в таком случае может пониматься как задача классификации динамических систем с точностью до отношений эквивалентности^{[источник?]}.

Способы задания динамических систем[править | править код]

Для задания динамической системы необходимо описать её фазовое пространство ${\displaystyle X}$, множество моментов времени ${\displaystyle T}$ и некоторое правило, описывающее движение точек фазового пространства со временем. Множество моментов времени ${\displaystyle T}$ может быть как интервалом вещественной прямой (тогда говорят, что время непрерывно), так и множеством целых или натуральных чисел (дискретное время). Во втором случае «движение» точки фазового пространства больше напоминает мгновенные «скачки» из одной точки в другую: траектория такой системы является не гладкой кривой, а просто множеством точек, и называется обычно орбитой. Тем не менее, несмотря на внешнее различие, между системами с непрерывным и дискретным временем имеется тесная связь: многие свойства являются общими для этих классов систем или легко переносятся с одного на другой.

Фазовые потоки[править | править код]

Пусть фазовое пространство ${\displaystyle X}$ представляет собой многомерное пространство или область в нем, а время непрерывно. Допустим, что нам известно, с какой скоростью движется каждая точка ${\displaystyle x}$ фазового пространства. Иными словами, известна вектор-функция скорости ${\displaystyle v(x)}$. Тогда траектория точки ${\displaystyle x_{0}\in X}$ будет решением автономного дифференциального уравнения ${\displaystyle {\frac {dx}{dt}}=v(x)}$ с начальным условием ${\displaystyle x(0)=x_{0}}$. Заданная таким образом динамическая система называется фазовым потоком для автономного дифференциального уравнения.

Каскады[править | править код]

Пусть ${\displaystyle X}$ — произвольное множество, и ${\displaystyle f\colon X\to X}$ — некоторое отображение множества ${\displaystyle X}$ на себя. Рассмотрим итерации этого отображения, то есть результаты его многократного применения к точкам фазового пространства. Они задают динамическую систему с фазовым пространством ${\displaystyle X}$ и множеством моментов времени ${\displaystyle T=\mathbb {N} }$. Действительно, будем считать, что произвольная точка ${\displaystyle x_{0}\in X}$ за время ${\displaystyle 1}$ переходит в точку ${\displaystyle x_{1}=f(x_{0})\in X}$. Тогда за время ${\displaystyle 2}$ эта точка перейдет в точку ${\displaystyle x_{2}=f(x_{1})=f(f(x_{0}))}$ и т. д.

Если отображение ${\displaystyle f}$ обратимо, можно определить и обратные итерации: ${\displaystyle x_{-1}=f^{-1}(x_{0})}$, ${\displaystyle x_{-2}=f^{-1}(f^{-1}(x_{0}))}$ и т. д. Тем самым получаем систему с множеством моментов времени ${\displaystyle T=\mathbb {Z} }$.

Примеры[править | править код]

• Система дифференциальных уравнений

${\displaystyle {\begin{cases}{\frac {dx}{dt}}=v\\{\frac {dv}{dt}}=-kx\end{cases}}}$

задает динамическую систему с непрерывным временем, называемую «гармоническим осциллятором». Её фазовым пространством является плоскость ${\displaystyle (x,v)}$, где ${\displaystyle v}$ — скорость точки ${\displaystyle x}$. Гармонический осциллятор моделирует разнообразные колебательные процессы — например, поведение груза на пружине. Его фазовыми кривыми являются эллипсы с центром в нуле.

• Пусть ${\displaystyle \varphi }$ — угол, задающий положение точки на единичной окружности. Отображение удвоения ${\displaystyle f(\varphi )=2\varphi {\pmod {2\pi }}}$, задаёт динамическую систему с дискретным временем, фазовым пространством которой является окружность.
• Быстро-медленные системы описывают процессы, одновременно развивающиеся в нескольких масштабах времени.
• Динамические системы, чьи уравнения могут быть получены посредством принципа наименьшего действия для удобно выбранного лагранжиана, известны как «лагранжевы динамические системы».

Вопросы теории динамических систем[править | править код]

Имея какое-то задание динамической системы, далеко не всегда можно найти и описать её траектории в явном виде. Поэтому обычно рассматриваются более простые (но не менее содержательные) вопросы об общем поведении системы. Например:

1. Есть ли у системы замкнутые фазовые кривые, то есть может ли она вернуться в начальное состояние в ходе эволюции?
2. Как устроены инвариантные многообразия системы (частным случаем которых являются замкнутые траектории)?
3. Как устроен аттрактор системы, то есть множество в фазовом пространстве, к которому стремится «большинство» траекторий?
4. Как ведут себя траектории, выпущенные из близких точек — остаются ли они близкими или уходят со временем на значительное расстояние?
5. Что можно сказать о поведении «типичной» динамической системы из некоторого класса?
6. Что можно сказать о поведении динамических систем, «близких» к данной?

Для улучшения этой статьи желательно: Оформить статью по правилам. Проставить сноски, внести более точные указания на источники. После исправления проблемы исключите её из списка. Удалите шаблон, если устранены все недостатки.

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

• Андронов А. А., Витт А. А., Хайкин С. Э. Теория колебаний. — 2-е изд., перераб. и испр.. — М.: Наука, 1981. — 918 с.
• Памяти Александра Александровича Андронова. — М.: Изд-во Академии наук СССР, 1955.
• Малинецкий Г. Г., Потапов А. Б., Подлазов А. В. Нелинейная динамика: подходы, результаты, надежды. — М.: УРСС, 2006.
• Гладкие динамические системы / ред. Д. В. Аносов. — М.: Мир, 1977. — 256 с.
• Евланов Л. Г. Контроль динамических систем. — М.: Наука, 1972. — 423 с. — 4800 экз.
• Биркгоф Дж. Динамические системы. — М.: ОГИЗ, 1999. — 480 с. — 3500 экз. — ISBN 5-7029-0356-0.

• Гукенхеймер Дж., Холмс Ф.^ru_en. Нелинейные колебания, динамические системы и бифуркации векторных полей. — 2002. — 560 с. — ISBN 5-93972-200-8.

• Палис Ж., ди Мелу В. Геометрическая теория динамических систем: Введение. — Мир, 1986. — 301 с.
• Шесть лекций по теории нелинейных динамических систем / Н. В. Карлов, Н. А. Кириченко. МФТИ, [1998?]. — 178 с. : ил.; 30 см; ISBN 5-7417-0096-9

Ссылки[править | править код]

• Weisstein, Eric W. Dynamical Systems (англ.) на сайте Wolfram MathWorld.