Distribuição normal – Wikipédia, a enciclopédia livre
| Teoria das probabilidades |
|---|
 |
| Distribuição Normal | |
|---|---|
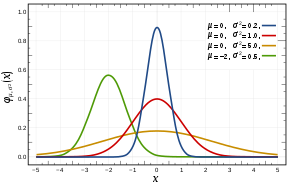 | |
A cor vermelha representa a função de densidade de probabilidade da distribuição normal padrão ~ N(0,1) | |
 | |
A cor vermelha representa a função de distribuição acumulada da distribuição normal padrão ~ N(0,1) | |
| Parâmetros | , média; , variância |
| Suporte | |
| f.d.p. | |
| f.d.a. | |
| Média | |
| Mediana | |
| Moda | |
| Variância | |
| Obliquidade | 0 |
| Curtose | 0 |
| Entropia | |
| Função Geradora de Momentos | |
| Função Característica | |
Em probabilidade e estatística, a distribuição normal é uma das distribuições de probabilidade mais utilizadas para modelar fenômenos naturais. Isso se deve ao fato de que um grande número de fenômenos naturais apresenta sua distribuição de probabilidade tão proximamente normal, que a ela pode ser com sucesso referida, e, portanto, com adequado acerto por ela representada como se normal fosse[1]. A distribuição normal é ligada a vários conceitos matemáticos como movimento browniano,[2] ruído branco,[3] entre outros. A distribuição normal também é chamada distribuição gaussiana, distribuição de Gauss ou distribuição de Laplace–Gauss, em referência aos matemáticos, físicos e astrônomos francês Pierre–Simon Laplace (1749 – 1827) e alemão Carl Friedrich Gauss (1777 – 1855).[4]

Em termos mais formais, a distribuição normal é uma distribuição de probabilidade absolutamente contínua parametrizada pela sua esperança matemática (número real ) e desvio padrão (número real positivo ). A densidade de probabilidade da distribuição normal é denotada como
- .
A distribuição normal com média nula e desvio padrão unitário é chamada de distribuição normal centrada e reduzida ou de distribuição normal padrão. Quando uma variável aleatória segue uma distribuição normal, ela é chamada de gaussiana ou de normal. Comumente é usada a notação com a variância quando A curva de densidade é chamada de curva de Gauss ou de curva em forma de sino.[5]
O papel central da distribuição normal decorre do fato de ser o limite de um grande número de distribuições de probabilidade como mostra o teorema central do limite, o qual permite estudar probabilisticamente a média das variáveis independentes de uma amostra aleatória simples de tamanho grande .[6] A distribuição normal corresponde ao comportamento do efeito agregado de experiências aleatórias independentes e semelhantes em certas circunstâncias quando o número de experiências é muito alto.[7] Com esta propriedade, a distribuição normal pode aproximar–se da distribuição de efeito agregado de outras distribuições e modelar vários estudos científicos como erros de medição ou testes estatísticos com as tabelas de distribuição normal.[8]
Histórico[editar | editar código-fonte]
Uma das primeiras aparições da distribuição normal ocorreu em 1733 com Abraham de Moivre com o aprofundamento do estudo de fatorial quando considerado um jogo de cara ou coroa.[9] Em 1756, ele publicou A Doutrina das Chances, em que a distribuição normal aparece como o limite de uma distribuição binomial, o que originaria o teorema central do limite.[10]
Em 1777, Pierre-Simon Laplace retomou o trabalho e obteve uma boa aproximação do erro entre a distribuição normal e a distribuição binomial em razão da função gama de Euler.[9] Em seu livro publicado em 1781, Laplace publica uma primeira tabela da distribuição normal. Em 1809, Carl Friedrich Gauss assimila os erros da observação na astronomia à curva, erros da densidade da distribuição normal.[10]
A distribuição normal é totalmente definida quando o primeiro teorema central do limite (chamado então teorema de Laplace) é elaborado por Laplace em 1821.[10] O nome normal é dado por Henri Poincaré no fim do século XIX.[11] A distribuição normal também pode ser chamada de distribuição de Gauss ou distribuição de Laplace–Gauss,[12] de acordo com sua autoria. A denominação segunda distribuição de Laplace também é usada ocasionalmente.[13][14]
A distribuição normal é estudada frequentemente. Por exemplo, novas tabelas digitais foram publicadas por Egon Sharpe Pearson em 1948, pelo National Bureau of Standards em 1952 e por Greenwood e Hartley em 1958.[15][16]
Distribuição normal padrão[editar | editar código-fonte]
Existe uma infinidade de distribuições normais, cada uma com sua própria média e desvio padrão. A distribuição normal com média 0 e desvio padrão 1 é chamada de distribuição normal padrão.[17] Ela é uma distribuição de probabilidade (uma medida , de massa total unitária) unidimensional (com suporte real ).[18] É uma distribuição absolutamente contínua (a medida é absolutamente contínua em relação à medida de Lebesgue).
Em outras palavras, existe uma densidade de probabilidade muitas vezes denotada como para a distribuição normal padrão tal que: . É generalizada para a distribuição normal multivariada. A distribuição normal padrão também pode ser chamada de distribuição normal centrada e reduzida.[19] A escala horizontal do gráfico da distribuição normal padrão corresponde ao escore-z que é uma medida de posição que indica o número de desvios padrão em que um valor se encontra a partir da média. Podemos transformar um valor em escore-z usando a fórmula:
Arredondar para o centésimo mais próximo
Quando um valor de uma variável aleatória distribuída normalmente é transformado em um escore-z, a distribuição de será uma distribuição normal padrão. Após essa transformação, a área que recai no intervalo sob a curva normal padrão é a mesma que aquela sob a curva normal padrão no correspondente intervalo .[20]
Propriedades da distribuição normal padrão[editar | editar código-fonte]
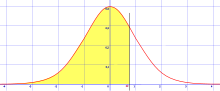
- A área acumulada é próxima de 0 para escores-z próximos a z=-3,49.
- A área acumulada aumenta conforme os escores-z aumentam.
- A área acumulada para z=0 é 0,5000.
- A área acumulada é próxima a 1 para escores-z próximos a z=3,49.
Definição pela função densidade[editar | editar código-fonte]

A densidade da distribuição normal padrão é dada pela função definida por , para todo .[21] Esta distribuição é chamada centrada porque o valor do seu momento de ordem 1 (esperança) é 0 e reduzida porque o valor do seu momento de ordem 2 (variância) é 1, assim como o seu desvio padrão. O gráfico da densidade é chamado função gaussiana, curva de Gauss ou curva em forma de
sino. A distribuição normal é denotada pela letra . Uma variável aleatória que segue uma distribuição normal padrão é denotada como .[22]
Seguem algumas propriedades sobre a função densidade:
- O cálculo da integral de Gauss permite demonstrar que a função é uma densidade de probabilidade pela fórmula .
- É contínua, uniformemente limitada e par.[23]
- O máximo da função é atingido na média 0 e de valor .[23]
- Verifica .[24]
- A densidade é infinitamente derivável. Uma indução matemática permite obter a fórmula para a -ésima derivada de : , em que é o –ésimo polinômio de Hermite.[25]
- A densidade possui dois pontos de inflexão, em 1 e em –1. Estes são os pontos em que a segunda derivada se anula e muda de sinal. Os dois pontos são aproximadamente três quintos da altura total.[18]
Definição pela função distribuição[editar | editar código-fonte]
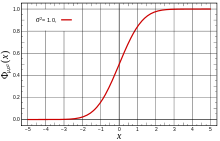
Historicamente a distribuição normal aparece como a distribuição limite no teorema central do limite, usando a função de distribuição cumulativa. A distribuição normal é a distribuição de probabilidade, em que a função de distribuição é dada por , definida por
, para todo . Ela fornece a probabilidade de uma variável aleatória de distribuição normal pertencer a
um intervalo fechado , .[26]
Seguem algumas propriedades sobre a função de distribuição:
- Não existe uma expressão analítica para a função de distribuição . Isto é, não é expressa a partir de funções usuais, mas torna–se uma função usual. Para obter os valores de probabilidade é preciso aproximar esta função de outras funções usuais gerando a tabela de valores.[27]
- Pode ser expressa em função da função erro por meio das seguintes fórmulas equivalentes e .[28]
- É infinitamente derivável e verifica . A fórmula equivalente permite definir a integral de Lebesgue–Stieltjes com relação à distribuição normal.[29]
- É absolutamente contínua e estritamente crescente, sendo uma bijeção de no intervalo aberto .[30] O recíproco é chamado de função inversa da função distribuição acumulada da distribuição normal. Por exemplo, esta função é utilizada pelo modelo probit.[31]
- Pela paridade da distribuição, . Portanto, . Isso mostra que a mediana da distribuição normal padrão é 0.[30]
Definição pela função característica[editar | editar código-fonte]

A caracterização da distribuição normal pela função característica tem o objetivo de demonstrar certas propriedades como a estabilidade da soma e o teorema central do limite. A função característica de distribuição normal padrão é dada por
e definida por , para todo .[32][33] Em grego existem duas variações para a letra phi minúscula. O utilizado agora é diferente do utilizado no início do texto. Isto é, são duas notações diferentes para phi minúsculo.
Esta função característica é proporcional à densidade da distribuição padrão. Ela permite demonstrar certas propriedades como a estabilidade por adição e o teorema central do limite.[34]
Seguem algumas propriedades sobre a função de distribuição:
- A função característica da distribuição normal pode ser obtida a partir da função densidade pelas igualdades .[26]
- Se uma variável aleatória segue uma distribuição normal padrão da função característica definida acima, então a transformação linear admite a função característica . É uma variável aleatória com distribuição normal de média e variância .[35]
Definição pela função geradora de momentos[editar | editar código-fonte]
Uma outra maneira de definir a distribuição normal padrão é pela utilização da função geradora de momentos. É a distribuição de probabilidade, em que a função geradora de momentos é dada por e definida por[36] , para todo . O objetivo é calcular os momentos da distribuição normal.[37]
Seguem algumas propriedades sobre a função geradora de momentos:
- A função geradora de momentos da distribuição normal pode ser obtida a partir da função densidade. Seja , que segue uma distribuição normal padrão, então .[36]
- Se uma variável aleatória segue uma distribuição normal padrão da função geradora de momentos , então a transformação linear admite a função geradora de momentos . Assim, é uma variável aleatória com distribuição normal de média e variância .[37]
Distribuição normal geral[editar | editar código-fonte]
Definição[editar | editar código-fonte]
Mais usualmente que a distribuição normal padrão, a distribuição normal não centrada e não reduzida é a distribuição de probabilidade absolutamente contínua, na qual um dos quatros pontos seguintes podem ser verificados.
- A densidade de probabilidade é dada pela função , definida por , para todo .[21]
- A função de distribuição (cumulativa) é dada pela função , definida por , para todo .[38]
- A função característica é dada por , definida por , para todo .[33]
- A função geradora de momentos é dada por , definida por , para todo ou e .[39]
Para , as funções de densidade e de distribuição não são definidas. Este caso corresponde a um comportamento degenerado da distribuição normal, às vezes chamada de distribuição normal imprópria. Isto é a medida de Dirac no ponto . O valor é a média da distribuição, é o desvio padrão e é a variância. Esta distribuição é denotada por , uma variável aleatória que segue a distribuição normal com a média e variância é denotada por .[33]
Observações[editar | editar código-fonte]
- Se a variável aleatória segue uma distribuição normal padrão , então a variável aleatória segue uma distribuição normal de média e de variância . Reciprocamente, se segue uma distribuição normal , então segue uma distribuição normal padrão.[40] Em outras palavras, toda distribuição normal pode ser obtida pela translação e pela dilatação de uma distribuição normal padrão. Esta primeira propriedade permite obter a fórmula .[41] Então, é possível deduzir as propriedades da distribuição normal a partir da distribuição normal centrada reduzida e vice–versa. A variável às vezes é chamada de padronização de ou de variável padrão .[42]
- A densidade é simétrica em relação à .[23]
- O máximo da função é atingido em , com valor .[23]
- Desde que a distribuição normal seja uma distribuição de probabilidade absolutamente contínua, o evento é insifgnificante. Isto é, quase certamente uma variável aleatória com distribuição normal nunca é igual a um valor fixo . Isto é expresso matematicamente por .[43]
- A largura à meia altura (largura da curva à metade da altura total) fornece um valor da amplitude da distribuição. Esta largura à meia altura da distribuição normal é proporcional ao desvio padrão . O fator 2 vem da propriedade de simetria da distribuição normal.[44]
- A densidade tem dois pontos de inflexão, em e em . Eles são os pontos, nos quais a segunda derivada anula–se e muda de sinal. Os dois pontos situam–se aproximadamente três quintos da altura total.[18]
- A distribuição normal é uma distribuição da família exponencial. Isto é, a sua densidade é escrita como ou como , com , , e .[45]
Propriedades[editar | editar código-fonte]
Outras caracterizações[editar | editar código-fonte]
Em adição à densidade de probabilidade, à função de distribuição, à função característica e à função geradora de momentos, existem outras caracterizações da distribuição normal.
- Caracterização segundo Georges Darmois e Sergeï Bernstein – se duas variáveis aleatórias e são independentes e igualmente distribuídas e se duas variáveis aleatórias e também são independentes, então a distribuição comum e é a distribuição normal.[10]
- Caracterização segundo Charles Stein – a distribuição normal é a única distribuição de probabilidade (medida de probabilidade) tal qual, para qualquer função de classe C¹ (derivável ou derivada contínua), [18]
Momentos[editar | editar código-fonte]
O momento de ordem 1 é chamado média () e é dado como parâmetro da distribuição normal . O segundo parâmetro é o desvio padrão (). Isto é, a raiz quadrada da variância , que é, por definição, a média dos quadrados dos desvios da média, ou segundo momento central. Os momentos centrais da distribuição normal são dados por,
para e uma variável aleatória com distribuição normal .[37]
O momento central de ordem pode ser obtido a partir de uma função de momentos de ordem inferior à e o momento de ordem pode ser obtido a partir de momentos de ordem inferior à – 1 e do momento central de ordem . Então, os primeiros momentos da distribuição normal são:
.[46]
Cálculo[editar | editar código-fonte]
Com a simetria em torno de da função densidade da distribuição normal, os momentos centrais de ordem ímpar são todos zero.[47] Os momentos de ordem par da distribuição normal padrão pode ser obtido pela relação de recorrência , que vem da integração por partes seguinte, para ,.[48]
É deduzida a fórmula dos momentos centrais reduzidos , assim a fórmula dos momentos centrais .[26]
Função geradora de momentos[editar | editar código-fonte]
Os momentos centrais de uma distribuição podem ser obtidos a partir da função geradora de momentos centrados. Para a distribuição , a mudança da variável permite obter as fórmulas de uma parte e de outra parte.[37]
Para a identificação dos coeficientes das duas séries, isto implica que os momentos de ordem ímpar são zero e fornece uma fórmula para os momentos de ordem par .[26]
Assimetria e curtose[editar | editar código-fonte]
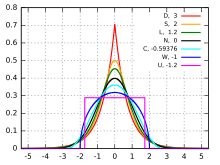
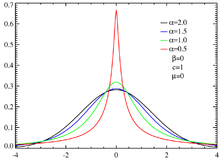
Densidades de probabilidade de distribuições com curtoses diferentes. Em vermelho, a distribuição de Laplace. Em laranja, a distribuição secante hiperbólica. Em verde, a distribuição logística. Em preto, a distribuição normal. Em cinza, a loi du cosinus surélevé. Em azul, a loi du demi-cercle. Em violeta, a distribuição uniforme.
A assimetria , a curtose e a curtose normalizada são obtidas a partir das fórmulas dos momentos .[49]
A distribuição normal é um ponto de referência para comparação das espessuras de caudas longas. Se uma distribuição possui uma curtose normalizada , então a distribuição possui uma cauda longa mais grossa que a distribuição normal e é chamada leptocúrtica. Se , a distribuição possui uma cauda longa mais fina que a distribuição normal e é chamada platicúrtica. Se a distribuição possui uma curtose normalizada nula, então a distribuição possui uma cauda longa comparável à distribuição normal e é chamada mesocúrtica.[50][51]
- Cumulantes
A função característica permite obter a função geradora de cumulantes pela fórmula e permite obter os cumulantes , e , para .[52]

Teoremas da convergência[editar | editar código-fonte]
A primeira versão do teorema central do limite (teorema de Moivre–Laplace) foi estabelecido para as variáveis aleatórias da distribuição de Bernoulli. De maneira mais geral, se são variáveis aleatórias independentes e igualmente distribuídas com variância finita e se a soma é denotada como , então , para todo , em que é a densidade de probabilidade da distribuição normal padrão.[27]
Este teorema significa que tudo que pode ser considerado a soma de um grande número de pequenos valores aleatórios independentes aproxima–se de uma distribuição normal.[53] Isto mostra a característica central da distribuição normal, em teoria da probabilidade. Um enunciado do teorema pode ser formulado como: se uma grandeza física submetida à influência de um número importante de fatores independentes e se a influência de cada fator separadamente é pequena, então a distribuição desta grandeza é uma distribuição gaussiana.[54]
O teorema central do limite é válido para toda distribuição de probabilidade com variáveis independentes e identicamente distribuídas que, com desvio padrão finito, permite obter uma boa aproximação da soma . Por exemplo,
- se as variáveis seguem a distribuição de Bernoulli , então segue aproximadamente uma distribuição normal . Esta aproximação é satisfatória quando ;[55]
- se as variáveis seguem a distribuição qui–quadrado com um graus de liberdade , então segue aproximadamente uma distribuição normal ;[56]
- se as variáveis seguem a distribuição exponencial , então segue aproximadamente uma distribuição normal .[57]
Existem versões mais gerais deste teorema. Por exemplo, variáveis aleatórias independentes não são da mesma distribuição, mas com pequenas variâncias em relação às suas médias.[58] Um teorema de Gnedenko e Kolmogorov (1954) estipula que uma variável aleatória normal é a soma de um grande número de variáveis aleatórias indenpendentes pequenas , sendo que nenhuma delas é predominante.[59]
Teorema – Seja uma série de variáveis aleatórias , sendo que cada uma é a soma de um número finito de variáveis aleatórias com . Para todo , introduz–se a variável aleatória truncada e supõe–se
Então, a distribuição de converge para a distribuição normal .[62]
Estabilidade e família normal[editar | editar código-fonte]
- Estabilidade pela adição (propriedade de conservação)
A distribuição normal é estável pela adição. Isto é, a soma de duas variáveis aleatórias independentes com distribuição normal é em si uma variável aleatória com distribuição normal. Mais explicitamente, se , e e são independentes, então a variável aleatória segue a distribuição normal .[10]
Esta propriedade é generalizada por variáveis, isto é, se para todo as variáveis aleatórias seguem a distribuição normal e são independentes, então a soma segue a distribuição normal .[63]
Esta propriedade é demonstrada diretamente por meio de funções características. A densidade de probabilidade da soma de duas variáveis aleatórias independentes da distribuição normal é dada pela convolução de duas densidades. Isto é traduzido pelas fórmulas de convolução de funções: ,[64]
ou de convolução de medidas normais denotadas como : . Não deve ser confundida com a distribuição, cuja densidade é a soma das densidades da distribuição normal.
Família normal[editar | editar código-fonte]
O conjunto de funções forma a chamada "família normal", que por sua vez também é o nome do conjunto de distribuições normais .[65] A família de funções está fechada para convolução no sentido que a função gera a família. Toda densidade que convolui um número suficientemente grande de vezes e adequadamente renormalizada está próxima de uma função de uma família normal.[64]
Os seguintes teoremas dão mais detalhes matemáticos:
- Se para uma função de densidade de média 0 e desvio padrão 1, e quaisquer e existe e , satisfazendo , então é a densidade da distribuição normal padrão.[66]
- De acordo com o teorema de Lévy–Cramér (1936), conjecturado por Paul Lévy, em 1935, se duas funções de densidade e verificam , então e com e . Em outras palavras, se a soma de duas variáveis aleatórias independentes é normal, então as duas variáveis aleatórias seguem a distribuição normal.[10][67]
- Se é a densidade comum de variáveis aleatórias independentes de média 0 e desvio padrão 1, então a convolução vezes de converge uniformemente em : (este teorema é equivalente ao teorema central do limite). Esta família normal não deve ser confundida com a família normal de funções holomorfas[64]
Estabilidade por linearidade[editar | editar código-fonte]
A distribuição normal é estável por linearidade. Se e são reais e , então a variável aleatória segue a distribuição normal .[68] Com a estabilidade por adição e por linearidade, a distribuição normal é um caso particular de distribuição estável com parâmetro de estabilidade .[69] Entre as distribuições estáveis, a distribuição normal, a distribuição de Lévy () e a distribuição de Cauchy () são as únicas com expressão analítica para a função densidade.[70]
Estabilidade pela média[editar | editar código-fonte]
A distribuição normal é estável pela média. Se são variáveis aleatórias independentes seguindo as distribuições normais , então a média segue a distribuição [71]
Convexidade[editar | editar código-fonte]
A distribuição normal não é convexa.[72] Isto é, a desigualdade , para todo e borelianos, não é satisfeita quando a medida é normal. Entretanto, quando a desigualdade é normalizada com o inverso da função de distribuição da distribuição normal padrão, obtém–se o teorema (desigualdade de Ehrhard) , para a medida padrão normal , todos os intervalos e e todo .[73]
Entropia e quantidade de informação[editar | editar código-fonte]
Entropia de Shannon[editar | editar código-fonte]
A entropia de Shannon de uma distribuição de probabilidade absolutamente contínua de densidade dada por para medir a quantidade de informação é definida por No conjuntos das distribuições absolutamente contínuas de variância fixa, as distribuições normais fornece entropia máxima.[74] A entropia para uma distribuição normal é dada por . Há também uma ligação entre a convergência de sequências de distribuições de probabilidade com distribuição normal e o aumento da entropia, tornando–se uma ferramenta importante na teoria da informação.[10]
Quantidade de informação de Fisher[editar | editar código-fonte]
A informação de Fisher de uma densidade de probabilidade é outro conceito de quantidade de informação. Para uma densidade , a informação de Fisher é dada por Para toda densidade suficientemente regular de uma distribuição normal padrão, a informação satisfaz a seguinte desigualdade: . A distribuição normal distingui–se de outras densidades desde que a desigualdade anterior seja uma igualdade e se e somente se a densidade for uma distribuição normal padrão.[10]
Distancia entre distribuições[editar | editar código-fonte]
A divergência de Kullback–Leibler permite medir a distância entre duas distribuições ou a perda de informação entre as duas distribuições. A divergência de Kullback–Leibler entre as duas distribuições normais e é .
Esta divergência é nula para e , mas aumenta quando também aumenta.[75]
Aproximação da função de distribuição[editar | editar código-fonte]
Não existe expressão analítica para a função de distribuição da distribuição normal padrão. Isto é, não existe uma fórmula simples entre a função de distribuição e as funções convencionais como as funções polinomiais, exponenciais, logarítmicas, trigonométricas, entre outras. Entretanto, a função de distribuição é aplicada a vários resultados e é importante compreende–la melhor. Diferentes notações como séries ou frações contínuas generalizadas são possíveis.[76]
Para , a função de distribuição da distribuição normal padrão é escrita na forma ou na forma [44]
Para , a função de distribuição da distribuição normal padrão é escrita na forma
De maneira mais numérica e facilmente calculável, as aproximações seguintes fornecem valores da função de distribuição da distribuição normal padrão com:
Em um exemplo de algoritmo para a linguagem C, uma outra notação da função de distribuição da distribuição normal padrão utiliza uma fração contínua generalizada: .[28]
Tabelas numéricas e cálculos[editar | editar código-fonte]

De acordo com a seção anterior, é útil saber a função de distribuição para aplicações numéricas. Então, tabelas de valores foram calculadas para a função de distribuição e também para o inverso da função de distribuição, que permitem obter os quantis e os intervalos de confiança para um limiar de tolerância fixo.[78]


 French
French Deutsch
Deutsch








































![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle \mathbb {P} (X\in [a,b])=\Phi (b)-\Phi (a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34021ca68e186eb6321321cf619fd9271e0c3129)





![{\displaystyle ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f6a83a50a400fb17f0c9abe6e674c6526a7b0e1)













![{\displaystyle M(t)=\mathbb {E} [e^{tX}]={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{+\infty }{\rm {e}}^{xt}{\rm {e}}^{-{\frac {x^{2}}{2}}}\mathrm {d} x={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{+\infty }{\rm {e}}^{-({\frac {(x-t)^{2}-t^{2}}{2}})}\mathrm {d} x={\rm {e}}^{\frac {t^{2}}{2}}\,{\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{+\infty }{\rm {e}}^{-{\frac {x^{2}}{2}}}\mathrm {d} x={\rm {e}}^{\frac {t^{2}}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3be141704e1e748c82a326f00e19ab163acac2fb)





















![{\displaystyle [X=x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9566107653e4195ce03e6a5ee53d35c52a946e35)


















![{\displaystyle {\begin{cases}\mu _{2k}=\mathbb {E} [(X-\mu )^{2k}]={\frac {(2\,k)!}{2^{k}k!}}\sigma ^{2k}\\\mu _{2k+1}=\mathbb {E} [(X-\mu )^{2k+1}]=0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd628c31049cf70f610ffc9f03b66f891c219593)

![{\displaystyle {\begin{cases}m_{1}=\mathbb {E} [X]=\mu \\m_{2}=\mathbb {E} [X^{2}]=\sigma ^{2}+\mu ^{2}\\m_{3}=\mathbb {E} [X^{3}]=3\mu \sigma ^{2}+\mu ^{3}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd3c79a314fb2d909d4aea408f046592a2b0792e)


























![{\displaystyle \lim _{n\rightarrow +\infty }\mathbb {P} \left(a\leq {\frac {S_{n}-\mathbb {E} [S_{n}]}{\sqrt {Var(S_{n})}}}\leq b\right)=\int _{a}^{b}\varphi (x)\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cda2b50bfd44cde85d74d7095091c8f7d543cf4f)
















![{\displaystyle \sum _{1\leq k\leq n}\mathbb {E} [X_{nk}^{\varepsilon }]{\underset {n\rightarrow \infty }{\longrightarrow }}\mu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/72572258880595c056c4a3ad951a5ef53030d20b)
![{\displaystyle \sum _{1\leq k\leq n}{\text{Var}}[X_{nk}^{\varepsilon }]{\underset {n\rightarrow \infty }{\longrightarrow }}\sigma ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45dd9047cd7a2ee62bd2ff254160438c5a4e7270)









































![{\displaystyle \lambda \in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/350ab5a5c7b6824da0369a91495c3733e9fc3e51)


























![{\displaystyle \Phi (x)=\mathbb {P} [X\leq x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b902c94ed7f70be63a1dc3bc78403187964686a)

![{\displaystyle \mathbb {P} [X\leq x]=\Phi (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95122ee20b4c0ef57ae4c372bd56c6fd59ce6403)