Diagrama de Venn – Wikipédia, a enciclopédia livre

Esta página ou se(c)ção precisa ser formatada para o padrão wiki. Por favor ajude a formatar esta página de acordo com as diretrizes estabelecidas. (Março de 2019)

Teoria das probabilidades
Axiomas de probabilidade
Espaço de probabilidade Espaço amostral Evento primário Evento Variável aleatória Medida de probabilidade
Evento complementar Eventos mutuamente exclusivos Probabilidade conjunta Probabilidade marginal Probabilidade condicional
Independência Independência condicional Lei da probabilidade total Lei dos grandes números Teorema de Bayes Desigualdade de Boole
Diagrama de Venn Diagrama de árvore
v d e

Designam-se por diagramas de Venn os diagramas usados em matemática para simbolizar graficamente propriedades, axiomas e problemas relativos aos conjuntos e sua teoria.

Os respectivos diagramas consistem de curvas fechadas simples desenhadas sobre um plano, de forma a simbolizar os conjuntos e permitir a representação das relações de pertença entre conjuntos e seus elementos (por exemplo, 4 ∈ {3,4,5}, mas 4 ∉ {1,2,3,12})^[1][2] e relações de continência (inclusão) entre os conjuntos (por exemplo, {1, 3} ⊂ {1, 2, 3, 4}).^[3][4] Assim, duas curvas que não se tocam e estão uma no espaço interno da outra simbolizam conjuntos que possuem continência; ao passo que o ponto interno a uma curva representa um elemento pertencente ao conjunto.^[5][6]

Do mesmo modo, espaços internos comuns a dois ou mais conjuntos representam a sua interseção, ao passo que a totalidade dos espaços pertencentes a um ou outro conjunto indistintamente representa sua união.

John Venn desenvolveu os diagramas no século XIX, ampliando e formalizando desenvolvimentos anteriores de Leibniz e Euler.^[7] E, na década de 1960, eles foram incorporados ao currículo escolar de matemática.^[8][9]

Embora seja simples construir diagramas de Venn para dois ou três conjuntos, surgem dificuldades quando se tenta usá-los para um número maior.^[10] Algumas construções possíveis são devidas ao próprio John Venn e a outros matemáticos como Anthony W. F. Edwards, Branko Grünbaum e Phillip Smith. Além disso, encontram-se em uso outros diagramas similares aos de Venn, entre os quais os de Euler, Johnston, Pierce e Karnaugh.^[11]

História[editar | editar código-fonte]

Os diagramas adotam o nome do seu criador John Venn, matemático e filósofo britânico do século XIX. Foi estudante e mais tarde professor no Caius College da Universidade de Cambridge, onde viria a desenvolver toda sua obra teórica.^[12]

Venn introduziu os diagramas em um trabalho de lógica formal publicado em Julho de 1880 na Philosophical Magazine and Journal of Science, intitulado Da representação mecânica e diagramática de proposições e raciocínios.^[5][13][14]

Embora a primeira forma de representação geométrica de silogismos seja frequentemente atribuída a Leibniz, e tenha sido retomada já durante o século XIX pelos matemáticos George Boole e Augustus De Morgan, o método de Venn superava os sistemas anteriores em termos de clareza e simplicidade, ao ponto de ser aceite como método padrão ao fim de algum tempo. Venn foi o primeiro a formalizar o seu uso e a dotá-lo de um mecanismo de generalização.^[12]

O próprio Venn não se referia aos diagramas como sendo da sua autoria, mas sim como círculos eulerianos, fazendo referência aos diagramas criados por Leonhard Euler no século XVIII.^[15] No parágrafo introdutório do seu artigo, Venn afirma:

Esquemas de representação diagramática tem sido tão familiarmente introduzidos nos tratados de lógica durante o último século que se pode supor que muitos leitores, mesmo aqueles que não fizeram qualquer estudo profissional de lógica, possam ter familiaridade com a noção geral de tais objetos. Dentre tais esquemas, apenas um - aquele comummente chamado 'círculos eulerianos', encontrou aceitação geral... (tradução livre)^[13]

Mais tarde, Venn desenvolveu o método no livro Lógica simbólica, publicado em 1881 com o objetivo de interpretar e corrigir os trabalhos de Boole no campo da lógica formal. Em 1889, publicou uma nova expansão de seu trabalho, com o livro Princípios da lógica empírica.^[12] A primeira referência escrita conhecida do termo Diagrama de Venn surge apenas em 1918, no livro de Clarence Irving Lewis, A Survey of Symbolic Logic.^[16][17]

No século XX, os diagramas de conjuntos passaram por novos desenvolvimentos. D. W. Henderson demonstrou em 1963 que a existência de um diagrama de Venn para N conjuntos com N eixos de simetria implica que N deve ser um número primo.^[18] Também demonstrou que tais diagramas simétricos existem quando N é 5 ou 7. Em 2002, Peter Hamburger encontrou diagramas simétricos para N = 11 e, em 2003, Griggs, Killian e Savage mostraram que diagramas simétricos existem para todos os outros primos.^[19]

A partir da década de 1960, os diagramas de Venn foram introduzidos no ensino escolar de matemática, na aprendizagem da teoria dos conjuntos e de funções, como parte do movimento da Matemática Moderna. Desde então, seu uso foi amplamente difundido, em áreas tão distintas como a compreensão de textos.^[9]

Diagramas[editar | editar código-fonte]

Os diagramas de Venn são feitos com coleções de curvas fechadas contidas em um plano. O interior dessas curvas representa, simbolicamente, a coleção de elementos do conjunto. De acordo com Clarence Irving Lewis, o "princípio desses diagramas é que classes [ou conjuntos] sejam representadas por regiões, com tal relação entre si que todas as relações lógicas possíveis entre as classes possam ser indicadas no mesmo diagrama. Isto é, o diagrama deixa espaço para qualquer relação possível entre as classes, e a relação dada ou existente pode então ser definida indicando se alguma região em específico é vazia ou não-vazia".^[20]

Pode-se escrever uma definição mais formal do seguinte modo: Seja ${\displaystyle {\textbf {C}}=(C_{1},C_{2},\ldots C_{n})}$ uma coleção de curvas fechadas simples desenhadas em um plano. C é uma família independente se a região formada por cada uma das interseções ${\displaystyle X_{1}\cap X_{2}\cap \ldots \cap X_{n}}$, onde cada ${\displaystyle X_{i}}$ é o interior ou o exterior de ${\displaystyle C_{i}}$, é não-vazia, em outras palavras, se todas as curvas se intersectam de todas as maneiras possíveis. Se, além disso, cada uma dessas regiões é conexa e há apenas um número finito de pontos de interseção entre as curvas, então C é um diagrama de Venn para n conjuntos.^[5][21]

Nos casos mais simples, os diagramas são representados por círculos que se encobrem parcialmente. As partes referidas em um enunciado específico são marcadas com uma cor diferente.^[5] Eventualmente, os círculos são representados como completamente inseridos dentro de um retângulo, que representa o conjunto universo daquele particular contexto (já se buscou a existência de um conjunto universo que pudesse abranger todos os conjuntos possíveis, mas Bertrand Russell mostrou que tal tarefa era impossível—ver paradoxo de Russell). A ideia de conjunto universo é normalmente atribuída a Lewis Carroll.^[22]

Dois conjuntos[editar | editar código-fonte]

Ver artigo principal: Conjunto#Operações com conjuntos

Considere-se o seguinte exemplo à direita: suponha-se que o conjunto A (círculo amarelo) representa os animais bípedes e o conjunto B (círculo azul) representa os animais capazes de voar. A área onde os dois círculos se sobrepõem, designada por interseção A e B ou interseção A-B, conteria todas as criaturas que ao mesmo tempo podem voar e têm apenas duas pernas motoras.

Considere-se agora que cada espécie viva está representada por um ponto situado em alguma parte do diagrama. Os humanos e os pinguins seriam marcados dentro do círculo laranja, na parte dele que não se sobrepõe com o círculo azul, já que ambos são bípedes mas não podem voar. Os mosquitos, que voam mas têm seis pernas, seriam representados dentro do círculo azul e fora da sobreposição. Os canários, por sua vez, seriam representados na interseção A-B, já que são bípedes e podem voar. Qualquer animal que não fosse bípede nem pudesse voar, como baleias ou serpentes, seria marcado por pontos fora dos dois círculos.

Assim, o diagrama de dois conjuntos representa quatro áreas distintas (a que fica fora de ambos os círculos, a parte de cada círculo que pertence a ambos os círculos (i.e. onde há sobreposição), e as duas áreas que não se sobrepõem, mas estão em um círculo ou no outro):^[23][24]

• Animais que possuem duas pernas e não voam (laranja sem sobreposição);
• Animais que voam e não possuem duas pernas (azul sem sobreposição);
• Animais que possuem duas pernas e voam (sobreposição);
• Animais que não possuem duas pernas e não voam (branco).

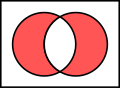
Essas configurações são representadas, respectivamente, pelas operações de conjuntos: diferença de A para B, diferença de B para A, interseção entre A e B, e conjunto complementar de A e B. Cada uma delas pode ser representada como as seguintes áreas vermelhas no diagrama:

• 
  Diferença
  de A para B:
  ${\displaystyle A\setminus B}$
• 
  Diferença
  de B para A:
  ${\displaystyle B\setminus A}$
• 
  Interseção de dois conjuntos:^[25]
  ${\displaystyle ~A\cap B}$
• 
  Complementar
  de dois conjuntos: ${\displaystyle U\setminus (A\cup B)}$

Além disso, essas quatro áreas podem ser combinadas de 16 formas diferentes.^[26] Por exemplo, pode-se perguntar sobre os animais que voam ou tem duas patas (pelo menos uma das características); tal conjunto seria representado pela união de A e B. Já os animais que voam e não possuem duas patas mais os que não voam e possuem duas patas, seriam representados pela diferença simétrica entre A e B. Estes exemplos são mostrados nas imagens a seguir, que incluem também outros dois casos.

• 
  União de dois conjuntos:^[25]
  ${\displaystyle ~A\cup B}$
• 
  Diferença simétrica
  de dois conjuntos: ${\displaystyle A~\Delta ~B}$
• 
  Complementar
  de A em U:${\displaystyle A^{c}~=~U\setminus A}$
• 
  Complementar
  de B em U: ${\displaystyle B^{c}~=~U\setminus B}$

Três conjuntos[editar | editar código-fonte]

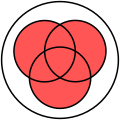
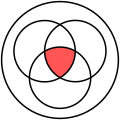
Na sua apresentação inicial, Venn focou-se sobretudo nos diagramas de três conjuntos.^[13] Alargando o exemplo anterior, poderia-se introduzir o conjunto C dos animais que possuem bico. Neste caso, o diagrama define oito áreas distintas (primeira imagem a seguir),^[23] que podem combinar-se de 256 (2⁸) maneiras diferentes,^[27] algumas delas ilustradas nas imagens seguintes.

• 
  Diagrama de Venn mostrando todas as interseções possíveis entre A, B e C.
• 
  União de três conjuntos:
  ${\displaystyle ~A\cup B\cup C}$
• 
  Interseção de três conjuntos:
  ${\displaystyle ~A\cap B\cap C}$
• 
  ${\displaystyle A\setminus (B\cup C)}$
• 
  ${\displaystyle (B\cup C)\setminus A}$

Extensões para mais conjuntos[editar | editar código-fonte]

Para representar quatro ou mais conjuntos, torna-se difícil fazer uma figura simples e simétrica que mostre todas as possibilidades de interseção. É fácil perceber que não é possível faze-lo apenas com círculos, sendo necessário recorrer a outras formas de representação gráfica.

Construção de Venn[editar | editar código-fonte]

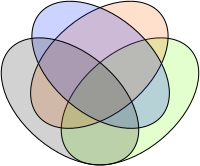
Ao longo da sua vida, Venn procurou encontrar formas de diagramas capazes de representar mais do que três conjuntos, a que se referia como "figuras simétricas ... elegantes por si só".^[13] A sua primeira representação para quatro conjuntos foi a interseção de elipses com base no diagrama de três círculos.^[13] Desenvolveu também um método geral para qualquer número de conjuntos, em que cada curva sucessiva delimita um conjunto que perpassa todos os outros.^[13]

• 
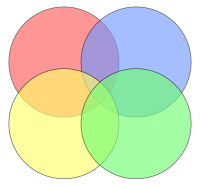
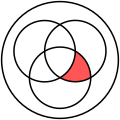
  O diagrama acima com quatro círculos não é um diagrama de Venn, porque nem todas as regiões possíveis são representadas. Por exemplo, não há uma região em que apenas o círculo azul e o amarelo se intersetem.
• 
  Construção de Venn para representar quatro conjuntos com quatro elipses.
• 
  Diagrama de Venn para cinco conjuntos usando elipses congruentes em um arranjo radialmente simétrico, desenvolvido por Branko Grünbaum. A legenda foi simplificada para melhorar a legibilidade. Por exemplo, A denota A ∩ B^c ∩ C^c ∩ D^c ∩ E^c (ou A ∩ ~B ∩ ~C ∩ ~D ∩ ~E), enquanto BCE denota A^c ∩ B ∩ C ∩ D^c ∩ E (ou ~A ∩ B ∩ C ∩ ~D ∩ E).
• 
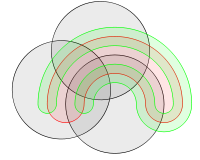
  Construção geral de Venn para 4 conjuntos
• 
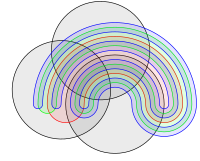
  Construção geral de Venn para 5 conjuntos
• 
  Construção geral de Venn para 6 conjuntos

Construção de Edwards[editar | editar código-fonte]

Anthony W. F. Edwards também desenvolveu um método para diagramas de Venn com números arbitrários de conjuntos, usando projeção estereográfica.^[28] Por exemplo, pode-se representar três conjuntos tomando três hemisférios de uma esfera, em ângulos retos (x=0, y=0 y z=0). Para adicionar um quarto conjunto, pode-se desenhar uma curva similar à junção de uma bola de tênis. Os conjuntos resultantes podem ser projetados novamente sobre o plano para mostrar diagramas de engrenagens, com quantidades cada vez maiores de dentes.^[29]

• 
  Diagrama de Edwards para três conjuntos.
• 
  Diagrama de Edwards para quatro conjuntos.
• 
  Diagrama de Edwards para cinco conjuntos.
• 
  Diagrama de Edwards para seis conjuntos.

Os diagramas de Edwards são topologicamente equivalentes aos diagramas desenhados por Branko Grünbaum, que se baseiam em polígonos intersetados, com quantidades crescentes de lados.^[21] Phillip Smith montou diagramas similares para n conjuntos, usando curvas senoidais em equações da forma y=sin(2ⁱx)/2ⁱ, 0 ≤i ≤n-2.^[30]

Representações com mais dimensões[editar | editar código-fonte]

Outra maneira de representar diagramas usando computadores é por meio de sólidos de dimensão superior.^[31] Abaixo, quatro esferas intersetadas, em uma figura completamente simétrica. As 16 interseções correspondem aos vértices de um tesserato.^[32]

Diagramas similares[editar | editar código-fonte]

Diagramas de Euler[editar | editar código-fonte]

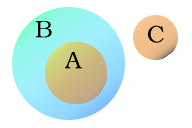
Os diagramas de Euler, criados antes dos diagramas de Venn,^[33] são similares a estes, usando normalmente círculos intersetados; sua diferença é que eles não precisam mostrar todas as possíveis relações, mas apenas as relações específicas de cada problema. Isso torna a representação, na maioria dos casos, visualmente mais simples.^[34]

Por exemplo, chamando-se de A o conjunto de todas as marcas de chocolate, de B todas as marcas de comida e de C todas as marcas de querosene, é fútil usar um diagrama de Venn. Sabe-se que todos os chocolates são comestíveis, então A é um subconjunto de B; por outro lado, sabe-se que nenhum querosene é comestível, então a interseção entre B e C (e consequentemente entre A e C) é nula. Assim, o diagrama de Euler ao lado é uma figura mais explicativa.

Diagrama de Johnston[editar | editar código-fonte]

Os diagramas de Johnston são visualmente iguais aos de Venn, mas, em vez de conjuntos, são utilizados para representar proposições e suas operações lógicas.^[36][37][38] Assim, sendo A e B duas sentenças, a interseção entre os círculos representa a sentença A e B, enquanto a união representa a sentença A ou B e o conjunto complementar a ambos representa nem A nem B.^[39][40]

Mapa de Karnaugh[editar | editar código-fonte]

Ver artigo principal: Mapa de Karnaugh

Os Mapas de Karnaugh ou Diagramas de Veitch são outra forma de representar visualmente expressões de álgebra booleana.^[41]

Diagrama de Peirce[editar | editar código-fonte]

Os diagramas de Peirce, criados por Charles Peirce, são extensões dos diagramas de Venn, que incluem informações sobre afirmações existenciais, disjuntivas, de probabilidade e outras.^[42]

Aplicações[editar | editar código-fonte]

Circuitos Digitais[editar | editar código-fonte]

O diagrama de Venn também é usado em Sistemas Digitais para a representação de funções lógicas de circuitos. Usamos o preenchimento colorido para representar onde o resultado da função será 1 (com energia), ou sem preenchimento quando o resultado for 0(sem energia). Onde temos:

• 
  Constante 1
• 
  Constante 0

Em sistemas digitais o diagrama de Venn é usado para a representação de circuitos, como:

S = (/A . B ) + C

O resultado dessa expressão utilizando o diagrama é obtido da seguinte maneira:

• 1º Passo: Fragmentar a expressão em varias expressões menores: S1 = (/A . B ) e S2 = C;
• 2º Passo: Montar o diagrama de Venn para S1 e S2:

• 
  S1 = /A . B
• 
  S2 = C

• 3º Passo: Unir os dois diagramas para chegar ao resultado da Expressão:

• 
  S = S1 + S2 = (/A . B ) + C

Seguindo esses três passos, conseguimos a representação gráfica do resultado de qualquer função logica.

Ver também[editar | editar código-fonte]

• Conjuntos
• Teoria dos conjuntos
• Diagrama
• Álgebra de Boole
• Teoria dos conjuntos

Referências

Ligações externas[editar | editar código-fonte]

O Commons possui uma categoria com imagens e outros ficheiros sobre Diagrama de Venn

• LogicTutorial.com: diagrama de Johnston interativo

Ferramentas para construir diagramas de Venn[editar | editar código-fonte]

• ConceptDraw
• InteractiVenn
• DrawVenn e DrawEuler
• 3 Circle Venn Diagram Applet
• VennDiagram.tk
• VennDiagrams
• Winvenn
• XFig Programa de desenho gráfico com licença GPL que gera vários códigos, incluindo LaTeX, EPS e PDF.