Geometria

La geometria (dal latino geometrĭa e questo dal greco antico: γεωμετρία?, composto dal prefisso geo- che rimanda alla parola greca γή = 'terra', 'terreno', e μετρία, metria, 'misura', quindi 'misurazione della Terra') è quella parte della matematica che si occupa delle forme nel piano e nello spazio, e delle loro mutue relazioni.

Storia[modifica | modifica wikitesto]
La nascita della geometria si fa risalire all'epoca degli antichi Egizi. Erodoto racconta che, a causa dei fenomeni di erosione e di deposito dovuti alle piene del Nilo, l'estensione delle proprietà terriere egiziane variavano ogni anno e dovevano quindi essere ricalcolate a fini fiscali. Nacque così il bisogno di inventare tecniche di misura della terra (geometria, nel significato originario del termine).
Lo sviluppo della geometria pratica è molto antico, per le numerose applicazioni che consente e per le quali è stata sviluppata, e in epoche remote fu a volte riservata a una categoria di sapienti con attribuzioni sacerdotali. Presso l'Antica Grecia, soprattutto per via dell'influenza del filosofo ateniese Platone e, ancor prima di lui, di Anassimandro di Mileto[senza fonte], si diffuse massicciamente l'uso della riga e del compasso (sebbene pare che questi strumenti fossero già stati inventati altrove) e, soprattutto, nacque l'idea nuova di usare tecniche dimostrative. La geometria greca servì da base per lo sviluppo della geografia, dell'astronomia, dell'ottica, della meccanica e di altre scienze, nonché di varie tecniche, come quelle per la navigazione.
Nella civiltà greca, oltre alla geometria euclidea che si studia ancora a scuola, e alla teoria delle coniche, nacquero anche la geometria sferica e la trigonometria (piana e sferica).
Geometria euclidea[modifica | modifica wikitesto]

La geometria coincide fino all'inizio del XIX secolo con la geometria euclidea. Questa definisce come concetti primitivi il punto, la retta e il piano, e assume la veridicità di alcuni assiomi, gli assiomi di Euclide. Da questi assiomi vengono quindi dedotti dei teoremi anche complessi, come il teorema di Pitagora ed i teoremi della geometria proiettiva.
La scelta dei concetti primitivi e degli assiomi è motivata dal desiderio di rappresentare la realtà, e in particolare gli oggetti nello spazio tridimensionale in cui viviamo. Concetti primitivi come la retta ed il piano vengono descritti informalmente come "fili e fogli di carta senza spessore", e d'altro canto molti oggetti della vita reale vengono idealizzati tramite enti geometrici come il triangolo o la piramide. In questo modo, i teoremi forniscono fin dall'antichità degli strumenti utili per le discipline che riguardano lo spazio in cui viviamo: meccanica, architettura, geografia, navigazione, astronomia.

Geometria piana[modifica | modifica wikitesto]
La geometria piana si occupa delle figure geometriche nel piano. A partire dal concetto primitivo di retta, vengono costruiti i segmenti, e quindi i poligoni come il triangolo, il quadrato, il pentagono, l'esagono, ecc.
Le quantità numeriche importanti nella geometria piana sono la lunghezza, l'angolo e l'area. Ogni segmento ha una lunghezza, e due segmenti che si incontrano in un estremo formano un angolo. Ogni poligono ha un'area. Molti teoremi della geometria piana mettono in relazione le lunghezze, angoli e aree presenti in alcune figure geometriche. Ad esempio, la somma degli angoli interni di un triangolo risulta essere un angolo piatto, e l'area di un rettangolo si esprime come prodotto delle lunghezze dei segmenti di base e altezza. La trigonometria studia le relazioni fra gli angoli e le lunghezze.
Geometria solida[modifica | modifica wikitesto]

La geometria solida (o stereometria) studia le costruzioni geometriche nello spazio. Con segmenti e poligoni si costruiscono i poliedri, come il tetraedro, il cubo e la piramide.
I poliedri hanno vertici, spigoli e facce. Ogni spigolo ha una lunghezza, ed ogni faccia ha un'area. In più, il poliedro ha un volume. Si parla inoltre di angoli diedrali per esprimere l'angolo formato da due facce adiacenti in uno spigolo. Molti teoremi mettono in relazione queste quantità: ad esempio il volume della piramide può essere espresso tramite l'area della figura di base e la lunghezza dell'altezza.

Figure curve[modifica | modifica wikitesto]
La geometria euclidea considera anche alcune figure curve. Le figure "base" sono la circonferenza nel piano e la sfera nello spazio, definite come luogo dei punti equidistanti da un punto fissato. Partendo da queste figure, ne vengono definite altre come il cono. A queste figure vengono associate grandezze analoghe ai poliedri: si parla quindi di lunghezza della circonferenza, di area del cerchio e di volume della sfera.
L'intersezione nello spazio di un cono con un piano forma una nuova figura curvilinea: a seconda dell'inclinazione del piano, questa è una ellisse, una parabola, un'iperbole o una circonferenza. Queste sezioni coniche sono le curve più semplici realizzabili nel piano. Ruotando una figura intorno ad una retta, si ottengono altre figure curve. Ad esempio, ruotando un'ellisse o una parabola si ottengono l'ellissoide ed il paraboloide. Anche in questo caso, il volume dell'oggetto può essere messo in relazione con altre quantità. La geometria euclidea non fornisce però sufficienti strumenti per dare una corretta definizione di lunghezza e area per molte figure curve.
Geometria cartesiana[modifica | modifica wikitesto]

La geometria cartesiana (o analitica) ingloba le figure ed i teoremi della geometria euclidea, introducendone di nuovi grazie a due altre importanti discipline della matematica: l'algebra e l'analisi. Lo spazio (ed il piano) sono rappresentati con delle coordinate cartesiane. In questo modo ogni figura geometrica è descrivibile tramite una o più equazioni (o disequazioni).
Rette e piani sono oggetti risultanti da equazioni di primo grado, mentre le coniche sono definite tramite equazioni di secondo grado. Equazioni polinomiali di grado superiore definiscono nuovi oggetti curvi. Il calcolo infinitesimale permette di estendere con precisione i concetti di lunghezza e area a queste nuove figure. L'integrale è un utile strumento analitico per determinare queste quantità. Si parla in generale quindi di curve e superfici nel piano e nello spazio.

Spazi vettoriali[modifica | modifica wikitesto]
Retta (passante per l'origine), piano (contenente l'origine) e spazio sono esempi di spazi vettoriali di dimensione rispettivamente 1, 2 e 3: infatti ogni punto è esprimile rispettivamente con 1, 2 o 3 coordinate. La geometria cartesiana è facilmente estendibile alle dimensioni superiori: in questo modo si definiscono spazi di dimensione 4 e oltre, come insiemi di punti aventi 4 o più coordinate.
Grazie all'algebra lineare, lo studio delle rette e dei piani nello spazio può essere esteso allo studio dei sottospazi di uno spazio vettoriale, di dimensione arbitraria. Lo studio di questi oggetti è strettamente collegato a quello dei sistemi lineari e delle loro soluzioni. In dimensione più alta, alcuni risultati possono contrastare con l'intuizione geometrica tridimensionale a cui siamo abituati. Ad esempio, in uno spazio di dimensione 4, due piani possono intersecarsi in un punto solo.
Geometria affine[modifica | modifica wikitesto]

In uno spazio vettoriale l'origine (cioè il punto da cui partono gli assi, di coordinate tutte nulle) gioca un ruolo fondamentale: per poter usare in modo efficace l'algebra lineare, si considerano infatti solo sottospazi passanti per l'origine. In questo modo si ottengono delle relazioni eleganti fra i sottospazi, come la formula di Grassmann.
Nella geometria affine il ruolo predominante dell'origine è abbandonato. I sottospazi non sono vincolati, e possono quindi essere paralleli: questo crea una quantità considerevole di casistiche in più. In particolare, la formula di Grassmann non è più valida. Lo spazio affine è considerato (fino alla scoperta della relatività ristretta) come lo strumento migliore per creare modelli dell'universo, con 3 dimensioni spaziali ed eventualmente 1 dimensione temporale, senza "origini" o punti privilegiati.
Geometria algebrica[modifica | modifica wikitesto]
Dal XIX secolo in poi l'algebra diventa uno strumento preponderante per lo studio della geometria. Nel tentativo di "abbellire" il quadro, e di ricondurre molte proprietà e teoremi ad un numero sempre minore di proprietà fondamentali, la geometria analitica viene progressivamente inglobata in un concetto più ampio di geometria: si aggiungono i "punti all'infinito" (creando così la geometria proiettiva), e si fanno variare le coordinate di un punto non solo nei numeri reali, ma anche in quelli complessi.

Geometria proiettiva[modifica | modifica wikitesto]
La geometria proiettiva nasce come strumento legato al disegno in prospettiva, e viene formalizzata nel XIX secolo come un arricchimento della geometria cartesiana. La geometria proiettiva include i "punti all'infinito" ed elimina quindi alcune casistiche considerate fastidiose, come la presenza di rette parallele.
In questa geometria molte situazioni si semplificano: due piani distinti si intersecano sempre in una retta, e oggetti differenti della geometria analitica (come le coniche ellisse, parabola e iperbole) risultano essere equivalenti in questo nuovo contesto. La geometria proiettiva è anche un esempio di compattificazione: similmente a quanto accade con la proiezione stereografica, aggiungendo i punti all'infinito lo spazio diventa compatto, cioè "limitato", "finito".

Varietà algebriche[modifica | modifica wikitesto]
La geometria algebrica verte essenzialmente sullo studio dei polinomi e delle loro radici: gli oggetti che tratta, chiamati varietà algebriche, sono gli insiemi dello spazio proiettivo, affine o euclideo definiti come luoghi di zeri di polinomi.
Nel XX secolo il concetto di varietà algebrica assume un'importanza sempre maggiore. Rette, piani, coniche, ellissoidi, sono tutti esempi di varietà algebriche. Lo studio di questi oggetti raggiunge risultati impressionanti quando le coordinate dello spazio vengono fatte variare nel campo dei numeri complessi: in questo caso, grazie al teorema fondamentale dell'algebra, un polinomio ha sempre delle radici.
Questo fatto algebrico di grande importanza (esprimibile dicendo che i numeri complessi formano un campo algebricamente chiuso) ha come conseguenza la validità di alcuni teoremi potenti di carattere molto generale. Ad esempio, il teorema di Bézout asserisce che due curve di grado e nel piano che non hanno componenti in comune si intersecano sempre in punti, contanti con un'opportuna molteplicità. Questo risultato necessita che il "piano" sia proiettivo e complesso. In particolare, è certamente falso nell'ambito classico della geometria analitica: due circonferenze non devono intersecarsi necessariamente in 4 punti, possono anche essere disgiunte.
Lo studio della geometria nello spazio proiettivo complesso aiuta anche a capire la geometria analitica classica. Le curve nel piano cartesiano reale possono ad esempio essere viste come "sezioni" di oggetti più grandi, contenuti nel piano proiettivo complesso, ed i teoremi generali validi in questo "mondo più vasto e perfetto" si riflettono nel piano cartesiano, pur in modo meno elegante. Come lo studio della geometria affine fa largo uso dell'algebra lineare, quello delle varietà algebriche attinge a piene mani dall'algebra commutativa.
Geometria differenziale[modifica | modifica wikitesto]
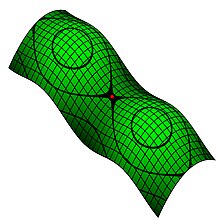
La geometria differenziale è lo studio di oggetti geometrici tramite l'analisi. Gli oggetti geometrici non sono necessariamente definiti da polinomi (come nella geometria algebrica), ma sono ad esempio curve e superfici, cioè oggetti che, visti localmente con una lente di ingrandimento, sembrano quasi rettilinei o piatti. Oggetti cioè "senza spessore", e magari un po' curvi. Come la superficie terrestre, che all'uomo sembra piatta, benché non lo sia.
Questo concetto di "spazio curvo" è espresso tramite la nozione di varietà differenziabile. La sua definizione non necessita neppure di "vivere" in uno spazio ambiente, ed è quindi usata ad esempio nella relatività generale per descrivere intrinsecamente la forma dell'universo. Una varietà può essere dotata di una proprietà fondamentale, la curvatura, che viene misurata tramite oggetti matematici molto complessi, come il tensore di Riemann. Nel caso in cui lo spazio sia una curva o una superficie, questi oggetti matematici risultano più semplici: si parla ad esempio di curvatura gaussiana per le superfici.
Su una varietà dotata di curvatura, detta varietà riemanniana, sono definite una distanza fra punti, e le geodetiche: queste sono curve che modellizzano i percorsi localmente più brevi, come le rette nel piano, o i meridiani sulla superficie terrestre.
Geometrie non euclidee[modifica | modifica wikitesto]

Con la geometria differenziale è possibile costruire un "piano" in cui valgono tutti i postulati di Euclide, tranne il quinto, quello delle parallele. Questo postulato ha avuto un'importanza storica fondamentale, perché ci sono voluti 2000 anni per dimostrare la sua effettiva indipendenza dai precedenti. Asserisce che, fissati una retta ed un punto non contenuto in , esiste un'unica retta parallela a e passante per .
Una geometria non euclidea è una geometria in cui valgono tutti gli assiomi di Euclide, tranne quello delle parallele. La sfera, con le geodetiche che giocano il ruolo delle rette, fornisce un esempio semplice di geometria non euclidea: due geodetiche si intersecano sempre in due punti antipodali, e quindi non ci sono rette parallele. Un tale esempio di geometria è detta ellittica. Esistono anche esempi opposti, in cui ci sono "così tante" rette parallele, che le rette parallele a e passanti per sono infinite (e non una). Questo tipo di geometria è detta iperbolica, ed è più difficile da descrivere concretamente.
Topologia[modifica | modifica wikitesto]

La topologia è infine lo studio delle forme, e di tutte quelle proprietà degli enti geometrici che non cambiano quando questi vengono deformati in modo continuo, senza strappi. La topologia studia tutti gli oggetti geometrici (definiti in modo algebrico, differenziale, o quant'altro) guardando solo la loro forma. Distingue ad esempio la sfera dal toro, perché quest'ultimo ha "un buco in mezzo". Studia le proprietà di connessione (spazi "fatti di un pezzo solo") e di compattezza (spazi "limitati"), e le funzioni continue fra questi.
Le forme degli oggetti vengono codificate tramite oggetti algebrici, come il gruppo fondamentale: un gruppo che codifica in modo raffinato la presenza di "buchi" in uno spazio topologico.
Geometria e geometrie[modifica | modifica wikitesto]

Nel 1872 Felix Klein elaborò un programma di ricerca, l'Erlanger Programm, in grado di produrre una grande sintesi delle conoscenze geometriche e integrarle con altri settori della matematica, quali la teoria dei gruppi.
Nella prospettiva di Klein una geometria consiste nello studio di proprietà di uno spazio che sono invarianti rispetto ad un gruppo di trasformazioni (geometria delle trasformazioni):
- La geometria euclidea si occupa di proprietà che sono invarianti rispetto a isometrie, cioè trasformazioni che preservano lunghezze e angoli.
- La geometria affine si occupa di proprietà che sono invarianti per trasformazioni affini. In ambito di geometria affine non ha più senso il concetto di "angolo" o di "lunghezza" e tutti i triangoli sono "equivalenti".
- La geometria proiettiva studia le proprietà che sono invarianti per trasformazioni proiettive, cioè trasformazioni che possono essere ottenute mediante proiezioni. In ambito proiettivo tutte le coniche sono equivalenti potendo essere trasformata l'una nell'altra da una proiezione.
- La topologia studia proprietà che sono invarianti per deformazioni continue. Dal punto di vista topologico una tazza ed una ciambella diventano equivalenti potendo essere deformate l'una nell'altra ma rimangono distinte da una sfera che non può essere "bucata" senza una trasformazione discontinua.
Applicazioni[modifica | modifica wikitesto]
La geometria analitica e l'algebra lineare forniscono importanti collegamenti tra l'intuizione geometrica e il calcolo algebrico che sono diventati ormai una parte costitutiva di tutta la matematica moderna e delle sue applicazioni in tutte le scienze. La geometria differenziale ha trovato importanti applicazioni nella costruzione di modelli per la fisica e per la cosmologia. La geometria piana e dello spazio fornisce inoltre degli strumenti per modellizzare, progettare e costruire oggetti reali nello spazio tridimensionale: è quindi di fondamentale importanza in architettura e in ingegneria come anche nel disegno e nella computer grafica.
Geometria descrittiva[modifica | modifica wikitesto]

La geometria descrittiva è una disciplina che permette, attraverso determinate costruzioni grafiche, di rappresentare oggetti tridimensionali già esistenti (rilievo) e/o da costruire (progettazione). L'applicazione informatizzata della geometria descrittiva permette oggi la creazione di superfici e solidi, anche ad alta complessità tridimensionale. Inoltre, e soprattutto, ne permette il controllo in modo inequivocabile di ogni loro forma e dimensione. I maggiori campi d'impiego della geometria descrittiva sono quelli dell'architettura, dell'ingegneria e quelli del design industriale.
Bibliografia[modifica | modifica wikitesto]
- Boris A. Dubrovin, Sergej P. Novikov, Anatolij T. Fomenko, Geometria contemporanea - metodi e applicazioni, suddivisa in:
- volume 1, Geometria delle superfici dei gruppi di trasformazioni e dei campi, Editori Riuniti, 2011. ISBN 978-88-6473-232-9
- volume 2, Geometria e topologia delle varietà, Editori Riuniti, 2011. ISBN 978-88-6473-233-6
- volume 3, Metodi della teoria delle omologie, Editori Riuniti, 2011. ISBN 978-88-6473-234-3
- Nikolai I. Lobachevsky, Pangeometry, traduction et édition: A. Papadopoulos, Heritage of European Mathematics Series, Vol. 4, European Mathematical Society, 2010.
- Robin Hartshorne, Geometry: Euclid and Beyond, Springer 2000, ISBN 0-387-98650-2
- Federigo Enriques, Questioni riguardanti la geometria elementare, Bologna Zanichelli 1900
- Federigo Enriques, Ugo Amaldi Elementi di Geometria ad uso delle scuole superiori, Zanichelli Bologna 1903 (ristampe fino al 1992)
- Federigo Enriques, Gli elementi di Euclide e la critica antica e moderna, 4 volumi, Roma e Bologna 1925
- Federigo Enriques, Lezioni di geometria descrittiva, Bologna 1893
- Guido Castelnuovo, Lezioni di geometria analitica e proiettiva, Roma, Milano, 1905
- Guido Castelnuovo, Elementi di geometria analitica e proiettiva Roma, 1909
- Emma Castelnuovo, La Geometria - La via della matematica, La nuova Italia, Firenze 1949 (ristampe fino al 1970)
- Giorgio Aprile, Mario Sciutto, La geometria, edizioni SEI, Torino 1963
Voci correlate[modifica | modifica wikitesto]
- Algebra
- Geometria analitica
- Geometria descrittiva
- Geometria non euclidea
- Geometria senza punti
- Grammatica geometrica
- Matematica
- Trigonometria
Altri progetti[modifica | modifica wikitesto]
 Wikiquote contiene citazioni sulla geometria
Wikiquote contiene citazioni sulla geometria Wikizionario contiene il lemma di dizionario «geometria»
Wikizionario contiene il lemma di dizionario «geometria» Wikiversità contiene risorse sulla geometria
Wikiversità contiene risorse sulla geometria Wikimedia Commons contiene immagini o altri file sulla geometria
Wikimedia Commons contiene immagini o altri file sulla geometria
Collegamenti esterni[modifica | modifica wikitesto]
- geometria, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
- Edoardo Vesentini, Geometria, in Enciclopedia della scienza e della tecnica, Istituto dell'Enciclopedia Italiana, 2007-2008.
- (EN) J.L. Heilbron, geometry, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- Geometria online Calcola automaticamente aree, perimetri, ecc. di figure piane e solide.
| Controllo di autorità | Thesaurus BNCF 6840 · LCCN (EN) sh85054133 · GND (DE) 4020236-7 · BNF (FR) cb119315301 (data) · J9U (EN, HE) 987007563084805171 · NDL (EN, JA) 00565738 |
|---|


 French
French Deutsch
Deutsch








