重合幾何 - 维基百科，自由的百科全书

在數學裡，重合幾何（incidence geometry）是研究重合結構的一門學科。歐氏平面之類的幾何是一個複雜的數學物件，包含長度、角度、連續性、中間性與重合關係。當其他的概念都被去掉，剩下的就只有「重合結構」，有關哪個點會位於哪條線上的資訊。即使有這樣嚴格的限制，還是有定理可被證明，而且存在著與此一結構有關之有趣事實。這樣的基本結論在其他概念被加回來形成較豐富的幾何時，仍然有效。有時，一些作者會搞混研究與研究的物件之間的不同之處，所以有些作者會將重合結構指為重合幾何，這並不令人意外^[1]。

重合結構會自然地出現於各個不同的數學領域之內，並已被許多人研究過。因此，存在著許多不同的詞彙用來描述此一物件。在圖論裡，重合結構被稱為超圖；而在組合設計理論裡，則被稱為區塊設計。除了詞彙的不同外，每個領域也以不同的方式處理此一物件，並對這些物件與該學科有關的一類問題感興趣。使用幾何的語言，如同在重合幾何內一般，形狀即時常會被作為主題與範例。不過，將其中一個學科裡的結論轉換成另一學科裡的用詞是可能的，雖然這往往會導致難以操作且令人費解的陳述，不像是該主題原本的一部分。在本條目裡，只會選擇使用能自然呈現幾何語言的範例。

其中最令人感興趣的例子為在歐氏平面上的有限點集合，可由重合結構決定線的數量與類型。因為只考慮重合性質，上述情形所得之部分結論可延伸至更一般的設定上。

重合結構[编辑]

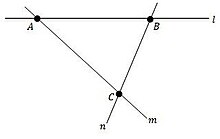
重合結構 $(P, L, I)$ 包含一個其元素被稱為「點」的集合 P、一個其元素被稱為「線」的不相交集合 L，以及兩個集合間的「重合關係」 I，即 P × L 的子集（其元素被稱為「標記」）^[2]。若 (A, l) 是一個標記，則稱 A 重合於 l 或 l 重合於 A（此一關係具對稱性），且寫作　A I l。直上，一個點與一條線在此一關係內，若且唯若該點位於該線上。給定一個點 B 與一條線 m，使其不組成一個標記，亦該點不位於該線上，則 (B, m) 被稱為「非標記」。

重合結構裡的距離[编辑]

重合結構裡並沒有距離（度量）的概念。不過，組合度量可存在於相對應的重合圖（勒維圖）裡，即為二分圖內兩個頂點間最短道路的長度。重合結構內兩個物件（兩個點、兩條線或一個點與一條線）的距離，可被定義為與重合結構相對應之重合圖內，對應之頂點間的距離。

另一種定義距離的方式，再度使用於圖論中的概念，此次為與重合結構相對應之「共線圖」。共線圖的頂點為重合結構的點，且兩個點互連，若存在一條線重合這兩個點。重合結構內兩個點的距離可定義為共線圖內兩個頂點的距離。

當於重合結構內考量距離時，有必要提及其定義方式。

部分線性空間[编辑]

最常被研究的重合結構會附加上一些額外的性質（公理），如投影平面、仿射平面、廣義多邊形、部分幾何與近多邊形等。極為一般的重合結構可透過附加「溫和」的條件取得，如：

部分線性空間為一重合結構，使得下列公理為真^[3]：

每對不同點至多決定一條線。
每條線至少包含兩個不同的點。

在部分線性空間裡，每對不同條線相交於至多一個點上。此一陳述不須作為公理的一部分，因為可由上述公理中簡單地被證明出來。

此外，可更進一步加上正則條件之限制：

RLk：每條線會重合的點之數量均相同。若該數為有限，通常標記為 k。

RPr：每個點會重合的線之數量均相同。若該數為有限，通常標記為 r。

部分線性空間的第二個公理蘊涵著 $k > 1$ 。兩個正則條件不會互相薀涵，所以必須假定 $r > 1$ 。

有限部分線性空間若滿足正則條件，且有限部分線性空間若滿足正則條件，且 k, r > 1，則稱之為「策略配置」（tactical configuration）^[4]。一些作者會簡單稱之為配置^[5]，或「投影配置」^[6]。若一策略配置有 n 個線與 m 條線，則透過重復計算標記，可建立 nr = mk 此一關係式，通常標記為 $(n r, m k)$ 配置。在 n = m （因此　r = k）時，　 $(n k, n k)$ 通常簡寫為 $(n k)$ 。

線性空間為一部分線性空間，使得^[7]：

每對不同點恰好決定一條線。

一些作者會在(部分)線性空間裡加上「非退化」（或「非平凡」）公理，如：

存在至少兩條不同的線^[8]。

這被用來排除一些非常小的例子（主要是集合 P 或 L 內少於2個元素之情形），這些例子通常會成為與重合結構有關之一般陳述的例外。另一種附加公理的方式為，將不符合公理的重合結構稱為「平凡」的；符合的則稱為「非平凡」的。

每個非平凡線性空間包含至少三個點與三條線，因此最簡單的非平凡線性空間為一三角形。

線性空間裡若每條線上至少有三個點，則稱之為西爾維斯特-加萊配置。

基本幾何例子[编辑]

重合幾何裡的一些基本概念與術語源自於幾何之中，尤其是仿射平面與投影平面。

投影平面[编辑]

「投影平面」是一個線性空間，使得：

每對不同的線會相交於恰好一個點上，

以及非退化條件：存在四個點，使得不存在三個這些點共線。

在投影平面裡，點 P 與線 L 間存在著對射。若 P 為一有限集合，該投影平面稱之為「有限」投影平面。有限投影平面的階為 n = k - 1，即線上的點之數量減一。所有已知的投影平面均有質數冪次的階。n 階投影平面為 $((n 2 + n + 1) n + 1)$ 配置。

最小的投影平面有二階，並被稱為「法諾平面」。

法諾平面[编辑]

此一著名的重合幾何係由義大利數學家基諾·法諾研究而得^[9]。在證明 n 維投影空間公理之獨立性的過程中^[10]，法諾發現了一個具15個點、35條線及15個平面的有限三維空間，其中每條線上有三個點^[11]。在這個空間裡的平面包含7個點與7條線，並被稱為法諾平面。

法諾平面無法於歐氏平面內只使用點與直線段來表示。這是西爾維斯特-加萊定理的結論。

一個完全四線形由四個點組成，沒有任何三個點共線。在法諾平面裡，除在完整四邊形裡的四個點外，另有三個完整四邊形的對角點，且這三個點共線。這違反了「法諾公理」。該公理通常被用來作為歐氏平面的公理，表示一完整四邊形的三個對角點絕不會共線。

仿射平面[编辑]

「仿射平面」是一個線性空間，使得：

對任一點 A 與不與該點重合的線 l（非標記）恰有一條與 A 重合（即　A I m），但不與 l 相交的線 m（稱之為普萊費爾公理）。

並滿足非退化條件：

存在一個三角形，即三個非共線的點。

在普萊費爾公理裡所述之線　l 與 m 被稱為是平行的。每個仿射平面均可唯一地被擴展成投影平面。有限仿射平面的「階」為 k，即一條線上點的數量。n 階仿射平面為 $((n 2) n + 1, (n 2 + n) n)$ 配置。

黑塞配置[编辑]

3階仿射平面為 $(9 4, 12 3)$ 配置。當嵌入一些周圍的空間時，稱之為黑塞配置。黑塞配置不可能在歐氏平面裡實現，但可於複投影平面裡實現，有9個橢圓曲線的反曲點及12條線，且每條線各與3個點重合。

這12條線可以分成4類，每類3條線。在各類中，線互不相交。這些類被稱為線的「平行類」。加上4個新的點，於各個平行類中的所有線上（所以現在所有線都相交）；以及一條新的線，只包括這4個新的點，即可形成3階投影平面，具 $(13 4)$ 配置。相反地，從（唯一一種）3階投影平面開始，移除任意一條線，以及所有在該線上的點，即可形成一個（唯一一種）3階仿射平面。

移除一個點並通過該點的4條線（但不包括其他在這些線上的點）會形成 $(8 3)$ 莫比烏斯-坎特配置。

部分幾何[编辑]

給定一整數 α ≥ 1，策略配置若滿足：對每個非標記 (B, m)，存在 α 個標記，使得 B I l 與 A I m，則稱之為「部分幾何」。若一條線上有 s+1 個點，且一個點上有 t+1 條線，則該部分幾何標記為 pg(s, t, α)。

若 α = 1，該部分幾何為廣義四邊形。

若 α = s + 1，該部分幾何為斯坦納系統。

廣義多邊形[编辑]

對 n > 2,^[12]，廣義 n 邊形是一個部分線性空間，其重合圖 Γ 具下列性質： Γ 的周長（最短環的長度）是　Γ　的直徑（兩個頂點間最長的距離，在此為　n）的兩倍。

「廣義2邊形」是一個重合結構，但不是部分線性空間，包括至少2個點與2條均與每個點重合的線。廣義2邊形的重合圖為一完整二分圖。

廣義 n 邊形不包含一般 m 邊形，其中 2 ≤ m < n；且對每一對物件（兩個點、兩條線或一個點與一條線），總存在一包含這兩個物件的一般 n 邊形。

廣義3邊形為投影平面，廣義4邊形稱為廣義四邊形。由范特-希格曼定理可知，具有每條線至少3個點與每個點至少3條線的有限廣義 n 邊形只有 n = 2、3、4、6 或 8 時的廣義多邊形。

近多邊形[编辑]

對一非負整數 d，近 2d 邊形是一重合結構，使得：

兩個點的最大距離（如在共線圖內量測）為 d，且
對每個點 X 與線 l，存在唯一個在 l 上且最接近 X 的點。

近 0 邊形為一個點，近 2 邊形為一條線。近 2 邊形的共線圖為一完全圖。近 4 邊形為一（可能退化的）廣義四邊形。每個廣義多邊形都是個近多邊形。任何連通二分圖均是近多邊形，且任一每條線上恰有2個點的近多邊形也都是連通二分圖。此外，所有的對偶極空間都是近多邊形。

一些近多邊形與有限簡單群有關。

莫比烏斯平面[编辑]

抽象莫比烏斯平面（或稱為反演平面）是一個重合結構，並為避免與傳統平面中的術語產生混淆，將之中的線稱之為「環」或「區塊」。

具體來說，莫比烏斯平面是一個點與環的重合結結，使得：

每三個不同點恰與一個環重合。
For any flag $(P, z)$ and any point $Q$ not incident with $z$ there is a unique cycle $z *$ with $P I z *, Q I z *$ and $z \cap z * = {P$ }. (The cycles are said to touch at $P$ .)
對任一標記　(P, z) 與任一不重合於 z 的點 Q，存在唯一個環 $z *$ ，使得 $P I z *$ 、 $Q I z *$ ，及 $z \cap z * = {P$ }（即這兩個環相交於　P）。
每個環有至少3個點，且至少存在一個環。

對莫比烏斯平面上的任一點 P，取 P 以外的其他所有點為點，以及僅包括 P 的環（並移除　P）為線，所得出之重合結構為一仿射平面。此一結構在設計理論中稱之為在　P 的「剩餘」。

m 階有限莫比烏斯平面具一策略配置，使得每個為 3-設計（具體來說，為　 $3-(m 2 + 1, m + 1, 1)$ 區塊設計）的環有 $k = m + 1$ 個點，

歐氏平面裡的重合定理[编辑]

西爾維斯特-加萊定理[编辑]

西爾維斯特-加萊定理是詹姆斯·約瑟夫·西爾維斯特提出一個與歐氏平面裡有限點集合之重合關係有關的問題，並由蒂博爾·由加萊提出解答。

西爾維斯特-加萊定理：歐氏平面上取一組有限多個點，這些點不是共線，就是存在一條線恰與其中的兩個點重合。

該條恰與其中的兩個點重合的線，在此稱為「一般線」。西爾維斯特在思索黑塞配置的嵌入性時，幾乎快解出這個問題。

迪布恩-艾狄胥定理[编辑]

相關的結論為迪布恩-艾狄胥定理。尼古拉斯·霍弗特·迪布恩與保羅·艾狄胥於更一般設定的投影平面上證明出此一結論，但於歐氏平面中亦仍然成立。該定理為^[13]：

於一投影平面上，每組非共線的　n 個點，可至少決定 n 條不同的線。

正如作者所指出的一般，因為他們的證明是組合的，此一結論在更大的設定，且實際上在任一重合幾何內均會成立。他們還提到，在歐氏平面上的定理可利用數學歸納法由西爾維斯特-加萊定理證得。

塞邁雷迪-托特定理[编辑]

一組有限的點與線所具有的標記數量之概估可由下列定理給出：

塞邁雷迪-托特定理：給定平面上的 n 個點與 m 條線，其標記（重合的對線對）之數量為：

O\left(n^{\frac {2}{3}}m^{\frac {2}{3}}+n+m\right),

而且，此一概估無法再更加精確。

此一結論可用來證明貝克定理。

貝克定理[编辑]

貝克定理表示，平面上任意有限多個點不是大部分的點會位於單一條線上，就是需要大量的線來連接所有的點。

該定理斷言，存在正實數 C、K，使得給定平面上任意 n 個點，下列陳述至少一個為真：

存在一條線包含至少n/C個這些點。
存在至少 n²/K 條線，使得每條線都包含至少兩個這些點。

在貝克原本的證明中，C 為100，而 K 則為一不確定的常數；但不知何值才是 C 與 K 的最優解。

另見[编辑]

組合設計
有限幾何
相交定理
勒維圖

註記[编辑]

^ As, for example, L. Storme does in his chapter on Finite Geometry in Colbourn & Dinitz (2007，pg. 702)
^ 技術上來看，這是個兩維的重合結構，其中維度是指考慮之物件類型數量（這裡為點與線）。也有人在研究更高維的結構，但一些作者會限定在兩維的情形，這裡也是如此。
^ Moorhouse，pg.5
^ Dembowski 1968，第5頁
^ Coxeter, H. S. M., Introduction to Geometry, New York: John Wiley & Sons: 233, 1969, ISBN 0-471-50458-0
^ Hilbert, David; Cohn-Vossen, Stephan, Geometry and the Imagination 2nd, Chelsea: 94–170, 1952, ISBN 0-8284-1087-9
^ Moorhouse，pg. 5
^ 亦有其他的「非平凡」公理，如Batten與Beutelspacher於1993年提出的公理，為「存在三個不在同一條線上的點」。另外還有其他的選擇，均為「存在」陳述，以排除一些過於簡單的例子。
^ Fano, G., Sui postulati fondamentali della geometria proiettiva, Giornale di Matematiche, 1892, 30: 106–132
^ Collino, Conte & Verra 2013，p. 6
^ Malkevitch Finite Geometries? an AMS Featured Column
^ n 邊形裡的「n」不應於配置內的點之數量搞混。
^ Weisstein, Eric W. （页面存档备份，存于互联网档案馆）, "de Bruijn–Erdős Theorem" （页面存档备份，存于互联网档案馆） from MathWorld Archive.is的存檔，存档日期2000-02-29

參考資料[编辑]

Batten, Lynn Margaret, Combinatorics of Finite Geometries, New York: Cambridge University Press, 1986, ISBN 0-521-31857-2

Batten, Lynn Margaret; Beutelspacher, Albrecht, The Theory of Finite Linear Spaces, New York: Cambridge University Press, 1993, ISBN 0-521-33317-2

Buekenhout, Francis (1995), Handbook of Incidence Geometry: Buildings and Foundations, Elsevier B.V.

Colbourn, Charles J.; Dinitz, Jeffrey H., Handbook of Combinatorial Designs 2nd, Boca Raton: Chapman & Hall/ CRC, 2007, ISBN 1-58488-506-8

Collino, Alberto; Conte, Alberto; Verra, Alessandro. On the life and scientific work of Gino Fano. 2013. arXiv:1311.7177 .

Dembowski, Peter, Finite geometries, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 44, Berlin, New York: Springer-Verlag, 1968, ISBN 3-540-61786-8, MR 0233275

Malkevitch, Joe. Finite Geometries?. [Dec 2, 2013]. （原始内容存档于2009-04-13）.

Moorhouse, G. Eric. Incidence Geometry (PDF). [Oct 20, 2012]. （原始内容 (PDF)存档于2013-10-29）.

Ueberberg, Johannes, Foundations of Incidence Geometry, Springer Monographs in Mathematics, Springer, 2011, ISBN 978-3-642-26960-8, doi:10.1007/978-3-642-20972-7 .

Shult, Ernest E., Points and Lines, Universitext, Springer, 2011, ISBN 978-3-642-15626-7, doi:10.1007/978-3-642-15627-4 .

外部連結[编辑]

incidence system （页面存档备份，存于互联网档案馆） at the Encyclopedia of Mathematics

[1] As, for example, L. Storme does in his chapter on Finite Geometry in Colbourn & Dinitz (2007，pg. 702)

[2] 技術上來看，這是個兩維的重合結構，其中維度是指考慮之物件類型數量（這裡為點與線）。也有人在研究更高維的結構，但一些作者會限定在兩維的情形，這裡也是如此。

[3] Moorhouse，pg.5

[4] Dembowski 1968，第5頁

[5] Coxeter, H. S. M., Introduction to Geometry, New York: John Wiley & Sons: 233, 1969, ISBN 0-471-50458-0

[6] Hilbert, David; Cohn-Vossen, Stephan, Geometry and the Imagination 2nd, Chelsea: 94–170, 1952, ISBN 0-8284-1087-9

[7] Moorhouse，pg. 5

[8] 亦有其他的「非平凡」公理，如Batten與Beutelspacher於1993年提出的公理，為「存在三個不在同一條線上的點」。另外還有其他的選擇，均為「存在」陳述，以排除一些過於簡單的例子。

[9] Fano, G., Sui postulati fondamentali della geometria proiettiva, Giornale di Matematiche, 1892, 30: 106–132

[10] Collino, Conte & Verra 2013，p. 6

[11] Malkevitch Finite Geometries? an AMS Featured Column

[12] 邊形裡的「n」不應於配置內的點之數量搞混。

[13] Weisstein, Eric W. （页面存档备份，存于互联网档案馆）, "de Bruijn–Erdős Theorem" （页面存档备份，存于互联网档案馆） from MathWorld Archive.is的存檔，存档日期2000-02-29

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]