Метод Ньютона — Википедия

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить ноль первой производной либо градиента в случае многомерного пространства.

Описание метода[править | править код]

Вывод[править | править код]

Чтобы численно решить уравнение ${\displaystyle f(x)=0}$ методом простой итерации, его необходимо привести к эквивалентному уравнению: ${\displaystyle x=\varphi (x)}$, где ${\displaystyle \varphi }$ — сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения ${\displaystyle x^{*}}$ должно выполняться условие ${\displaystyle \varphi '(x^{*})=0}$. Решение данного уравнения ищут в виде ${\displaystyle \varphi (x)=x+\alpha (x)f(x)}$, тогда:

${\displaystyle \varphi '(x^{*})=1+\alpha '(x^{*})f(x^{*})+\alpha (x^{*})f'(x^{*})=0.}$

В предположении, что точка приближения «достаточно близка» к корню ${\displaystyle {\tilde {x}}}$ и что заданная функция непрерывна ${\displaystyle (f(x^{*})\approx f({\tilde {x}})=0)}$, окончательная формула для ${\displaystyle \alpha (x)}$ такова:

${\displaystyle \alpha (x)=-{\frac {1}{f'(x)}}.}$

С учётом этого функция ${\displaystyle \varphi (x)}$ определяется:

${\displaystyle \varphi (x)=x-{\frac {f(x)}{f'(x)}}.}$

При некоторых условиях эта функция в окрестности корня осуществляет сжимающее отображение.

В этом случае алгоритм нахождения численного решения уравнения ${\displaystyle f(x)=0}$ сводится к итерационной процедуре вычисления:

${\displaystyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.}$

По теореме Банаха последовательность приближений стремится к корню уравнения ${\displaystyle f(x)=0}$.

Геометрическая интерпретация[править | править код]

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к графику исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Пусть 1) вещественнозначная функция ${\displaystyle f(x)\colon (a,\,b)\to \mathbb {R} }$ непрерывно дифференцируема на интервале ${\displaystyle (a,\,b)}$ ;
2) существует искомая точка ${\displaystyle x^{*}\in (a,\,b)}$ : ${\displaystyle f(x^{*})=0}$ ;
3) существуют ${\displaystyle C>0}$ и ${\displaystyle \delta >0}$ такие, что
${\displaystyle \vert f'(x)\vert \geqslant C}$ для ${\displaystyle x\in (a,\,x^{*}-\delta ]\cup [x^{*}+\delta ,\,b)}$
и ${\displaystyle f'(x)\neq 0}$ для ${\displaystyle x\in (x^{*}-\delta ,\,x^{*})\cup (x^{*},\,x^{*}+\delta )}$ ;
4) точка ${\displaystyle x_{n}\in (a,\,b)}$ такова, что ${\displaystyle f(x_{n})\neq 0}$ .
Тогда формула итеративного приближения ${\displaystyle x_{n}}$ к ${\displaystyle x^{*}}$ может быть выведена из геометрического смысла касательной следующим образом:

${\displaystyle f'(x_{n})=\mathrm {tg} \,\alpha _{n}={\frac {\Delta y}{\Delta x}}={\frac {f(x_{n})-0}{x_{n}-x_{n+1}}}={\frac {0-f(x_{n})}{x_{n+1}-x_{n}}},}$

где ${\displaystyle \alpha _{n}}$ — угол наклона касательной прямой ${\displaystyle y(x)=f(x_{n})+(x-x_{n})\cdot \mathrm {tg} \,\alpha _{n}}$ к графику ${\displaystyle f}$ в точке ${\displaystyle (x_{n};f(x_{n}))}$ .

Следовательно (в уравнении касательной прямой полагаем ${\displaystyle y(x_{n+1})=0}$) искомое выражение для ${\displaystyle x_{n+1}}$ имеет вид :

${\displaystyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.}$

Если ${\displaystyle x_{n+1}\in (a,\,b)}$, то это значение можно использовать в качестве следующего приближения к ${\displaystyle x^{*}}$ .

Если ${\displaystyle x_{n+1}\notin (a,\,b)}$, то имеет место «перелёт» (корень ${\displaystyle x^{*}}$ лежит рядом с границей ${\displaystyle (a,\,b)}$). В этом случае надо (воспользовавшись идеей метода половинного деления) заменять ${\displaystyle x_{n+1}}$ на ${\displaystyle {\frac {x_{n}+x_{n+1}}{2}}}$ до тех пор, пока точка «не вернётся» в область поиска ${\displaystyle (a,\,b)}$ .

Замечания. 1) Наличие непрерывной производной даёт возможность строить непрерывно меняющуюся касательную на всей области поиска решения ${\displaystyle (a,\,b)\;}$ .
2) Случаи граничного (в точке ${\displaystyle a}$ или в точке ${\displaystyle b}$) расположения искомого решения ${\displaystyle x^{*}}$ рассматриваются аналогичным образом.
3) С геометрической точки зрения равенство ${\displaystyle f'(x_{n})=0}$ означает, что касательная прямая к графику ${\displaystyle f}$ в точке ${\displaystyle (x_{n};f(x_{n}))}$ - параллельна оси ${\displaystyle OX}$ и при ${\displaystyle f(x_{n})\neq 0}$ не пересекается с ней в конечной части.
4) Чем больше константа ${\displaystyle C>0}$ и чем меньше константа ${\displaystyle \delta >0}$ из пункта 3 условий, тем для ${\displaystyle x_{n}\in (a,\,x^{*}-\delta ]\cup [x^{*}+\delta ,\,b)}$ пересечение касательной к графику ${\displaystyle f}$ и оси ${\displaystyle OX}$ ближе к точке ${\displaystyle (x^{*};\;0)}$ , то есть тем ближе значение ${\displaystyle x_{n+1}}$ к искомой ${\displaystyle x^{*}\in (a,\,b)}$ .

Итерационный процесс начинается с некоторого начального приближения ${\displaystyle x_{0}\in (a,\,b)}$ , причём между ${\displaystyle x_{0}\in (a,\,b)}$ и искомой точкой ${\displaystyle x^{*}\in (a,\,b)}$ не должно быть других нулей функции ${\displaystyle f}$ , то есть «чем ближе ${\displaystyle x_{0}}$ к искомому корню ${\displaystyle x^{*}}$ , тем лучше». Если предположения о нахождении ${\displaystyle x^{*}}$ отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях.

Для предварительно заданных ${\displaystyle \varepsilon _{x}>0}$ , ${\displaystyle \varepsilon _{f}>0}$ итерационный процесс завершается если ${\displaystyle \left\vert {\frac {f(x_{n})}{f'(x_{n})}}\right\vert \approx \vert x_{n+1}-x_{n}\vert <\varepsilon _{x}}$ и ${\displaystyle \vert f(x_{n+1})\vert <\varepsilon _{f}}$ .
В частности, для матрицы дисплея ${\displaystyle \varepsilon _{x}}$ и ${\displaystyle \varepsilon _{f}}$ могут быть рассчитаны, исходя из масштаба отображения графика ${\displaystyle f}$ , то есть если ${\displaystyle x_{n}}$ и ${\displaystyle x_{n+1}}$ попадают в один вертикальный, а ${\displaystyle f(x_{n})}$ и ${\displaystyle f(x_{n+1})}$ в один горизонтальный ряд.

Алгоритм[править | править код]

1. Задается начальное приближение ${\displaystyle x_{0}}$.
2. Пока не выполнено условие остановки, в качестве которого следует взять ${\displaystyle \left\vert {\frac {x_{n+1}-x_{n}}{1-{\frac {x_{n+1}-x_{n}}{x_{n}-x_{n-1}}}}}\right\vert <\varepsilon }$, где ${\displaystyle \varepsilon }$ выполняет роль абсолютной погрешности (так как метод Ньютона является частным случаем метода простой итерации^[1]), вычисляют новое приближение: ${\displaystyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}}$.

Пример[править | править код]

Иллюстрация применения метода Ньютона к функции ${\displaystyle f(x)=\cos x-x^{3}}$ с начальным приближением в точке ${\displaystyle x_{0}=0{,}5}$.
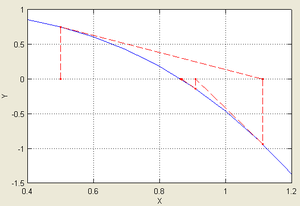Согласно способу практического определения скорость сходимости может быть оценена как тангенс угла наклона графика сходимости, то есть в данном случае равна двум.

Рассмотрим задачу о нахождении положительных ${\displaystyle x}$, для которых ${\displaystyle \cos x=x^{3}}$. Эта задача может быть представлена как задача нахождения нуля функции ${\displaystyle f(x)=\cos x-x^{3}}$. Имеем выражение для производной ${\displaystyle f'(x)=-\sin x-3x^{2}}$. Так как ${\displaystyle \cos x\leqslant 1}$ для всех ${\displaystyle x}$ и ${\displaystyle x^{3}>1}$ для ${\displaystyle x>1}$, очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение ${\displaystyle x_{0}=0{,}5}$, тогда:

${\displaystyle {\begin{matrix}x_{1}&=&x_{0}-{\dfrac {f(x_{0})}{f'(x_{0})}}&=&1{,}112\;141\;637\;097,\\x_{2}&=&x_{1}-{\dfrac {f(x_{1})}{f'(x_{1})}}&=&{\underline {0{,}}}909\;672\;693\;736,\\x_{3}&=&x_{2}-{\dfrac {f(x_{2})}{f'(x_{2})}}&=&{\underline {0{,}86}}7\;263\;818\;209,\\x_{4}&=&x_{3}-{\dfrac {f(x_{3})}{f'(x_{3})}}&=&{\underline {0{,}865\;47}}7\;135\;298,\\x_{5}&=&x_{4}-{\dfrac {f(x_{4})}{f'(x_{4})}}&=&{\underline {0{,}865\;474\;033\;1}}11,\\x_{6}&=&x_{5}-{\dfrac {f(x_{5})}{f'(x_{5})}}&=&{\underline {0{,}865\;474\;033\;102}}.\end{matrix}}}$

Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.

Условия применения[править | править код]

Рассмотрим ряд примеров, указывающих на недостатки метода.

Контрпримеры[править | править код]

• Если начальное приближение недостаточно близко к решению, то метод может не сойтись.

Пусть

${\displaystyle f(x)=x^{3}-2x+2.}$

Тогда

${\displaystyle x_{n+1}=x_{n}-{\frac {x_{n}^{3}-2x_{n}+2}{3x_{n}^{2}-2}}.}$

Возьмём ноль в качестве начального приближения. Первая итерация даст в качестве приближения единицу. В свою очередь, вторая снова даст ноль. Метод зациклится и решение не будет найдено. В общем случае построение последовательности приближений может быть очень запутанным.

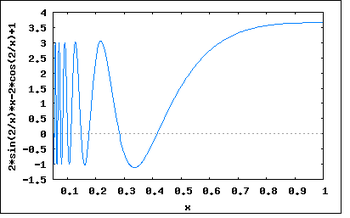
• Если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня.

Рассмотрим функцию:

${\displaystyle f(x)={\begin{cases}0,&x=0,\\x+x^{2}\sin \left({\dfrac {2}{x}}\right),&x\neq 0.\end{cases}}}$

Тогда ${\displaystyle f'(0)=1}$ и ${\displaystyle f'(x)=1+2x\sin(2/x)-2\cos(2/x)}$ всюду, кроме 0.

В окрестности корня производная меняет знак при приближении ${\displaystyle x}$ к нулю справа или слева. В то время, как ${\displaystyle f(x)\geqslant x-x^{2}>0}$ для ${\displaystyle 0<x<1}$.

Таким образом ${\displaystyle f(x)/f'(x)}$ не ограничено вблизи корня, и метод будет расходиться, хотя функция всюду дифференцируема, её производная не равна нулю в корне, ${\displaystyle f}$ бесконечно дифференцируема везде, кроме как в корне, а её производная ограничена в окрестности корня.

• Если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена.

Рассмотрим пример:

${\displaystyle f(x)=x+x^{4/3}.}$

Тогда ${\displaystyle f'(x)=1+(4/3)x^{1/3}}$ и ${\displaystyle f''(x)=(4/9)x^{-2/3}}$ за исключением ${\displaystyle x=0}$, где она не определена.

На очередном шаге имеем ${\displaystyle x_{n}}$:

${\displaystyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}={\frac {(1/3)x_{n}^{4/3}}{(1+(4/3)x_{n}^{1/3})}}.}$

Скорость сходимости полученной последовательности составляет приблизительно 4/3. Это существенно меньше, нежели 2, необходимое для квадратичной сходимости, поэтому в данном случае можно говорить лишь о линейной сходимости, хотя функция всюду непрерывно дифференцируема, производная в корне не равна нулю, и ${\displaystyle f}$ бесконечно дифференцируема везде, кроме как в корне.

• Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.

Пусть

${\displaystyle f(x)=x^{2}.}$

Тогда ${\displaystyle f'(x)=2x}$ и следовательно ${\displaystyle x-f(x)/f'(x)=x/2}$. Таким образом сходимость метода не квадратичная, а линейная, хотя функция всюду бесконечно дифференцируема.

Ограничения[править | править код]

Пусть задано уравнение ${\displaystyle f(x)=0}$, где ${\displaystyle f(x)\colon \mathbb {X} \to \mathbb {R} }$ и надо найти его решение.

Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Она носит имя советского математика и экономиста Леонида Витальевича Канторовича (1912—1986).

Теорема Канторовича.

Если существуют такие константы ${\displaystyle A,\;B,\;C}$, что:

1. ${\displaystyle {\frac {1}{|f'(x)|}}<A}$ на ${\displaystyle [a,\;b]}$, то есть ${\displaystyle f'(x)}$ существует и не равна нулю;
2. ${\displaystyle \left|{\frac {f(x)}{f'(x)}}\right|<B}$ на ${\displaystyle [a,\;b]}$, то есть ${\displaystyle f(x)}$ ограничена;
3. ${\displaystyle \exists f''(x)}$ на ${\displaystyle [a,\;b]}$, и ${\displaystyle |f''(x)|\leqslant C\leqslant {\frac {1}{2AB}}}$;

Причём длина рассматриваемого отрезка ${\displaystyle |a-b|<{\frac {1}{AB}}\left(1-{\sqrt {1-2ABC}}\right)}$. Тогда справедливы следующие утверждения:

1. на ${\displaystyle [a,\;b]}$ существует корень ${\displaystyle x^{*}}$ уравнения ${\displaystyle f(x)=0\colon \exists x^{*}\in [a,\;b]\colon f(x^{*})=0}$;
2. если ${\displaystyle x_{0}={\frac {a+b}{2}}}$, то итерационная последовательность сходится к этому корню: ${\displaystyle \left\{x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}\right\}\to x^{*}}$;
3. погрешность может быть оценена по формуле ${\displaystyle |x^{*}-x_{n}|\leqslant {\frac {B}{2^{n-1}}}(2ABC)^{2^{n-1}}}$.

Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:

${\displaystyle |x^{*}-x_{n}|\leqslant {\frac {B}{2^{n-1}}}(2ABC)^{2^{n-1}}={\frac {1}{2}}{\frac {B}{2^{n-2}}}\left((2ABC)^{2^{n-2}}\right)^{2}=\alpha |x^{*}-x_{n-1}|^{2}.}$

Тогда ограничения на исходную функцию ${\displaystyle f(x)}$ будут выглядеть так:

1. функция должна быть ограничена;
2. функция должна быть гладкой, дважды дифференцируемой;
3. её первая производная ${\displaystyle f'(x)}$ равномерно отделена от нуля;
4. её вторая производная ${\displaystyle f''(x)}$ должна быть равномерно ограничена.

Историческая справка[править | править код]

Метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» (лат. «De analysi per aequationes numero terminorum infinitas»), адресованной в 1669 году Барроу, и в работе «Метод флюксий и бесконечные ряды» (лат. «De metodis fluxionum et serierum infinitarum») или «Аналитическая геометрия» (лат. «Geometria analytica») в собраниях трудов Ньютона, которая была написана в 1671 году. В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения ${\displaystyle x_{n}}$, а последовательность полиномов и в результате получал приближённое решение ${\displaystyle x}$.

Этот же метод применён Ньютоном в его трактате "Математические начала" для решения уравнения Кеплера, где Ньютон предложил вполне современную аналитическую форму вычисления, записав последовательность приближений в виде переразлагаемого в каждой новой точке аналитического ряда:

ряд ... сходится настолько быстро, что едва ли когда-нибудь понадобится идти в нём далее второго члена ...

— ^[2]

Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе «Общий анализ уравнений» (лат. «Analysis aequationum universalis»). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений ${\displaystyle x_{n}}$ вместо более трудной для понимания последовательности полиномов, использованной Ньютоном. Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.

В 1879 году Артур Кэли в работе «Проблема комплексных чисел Ньютона — Фурье» (англ. «The Newton-Fourier imaginary problem») был первым, кто отметил трудности в обобщении метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов.

Обобщения и модификации[править | править код]

Метод секущих[править | править код]

Родственный метод секущих является «приближённым» методом Ньютона и позволяет не вычислять производную. Значение производной в итерационной формуле заменяется её оценкой по двум предыдущим точкам итераций:

${\displaystyle f'(x_{n})\approx {\frac {f(x_{n})-f(x_{n-1})}{x_{n}-x_{n-1}}}}$ .

Таким образом, основная формула имеет вид

${\displaystyle x_{n+1}=x_{n}-f(x_{n})\cdot {\frac {x_{n}-x_{n-1}}{f(x_{n})-f(x_{n-1})}}.}$

Этот метод схож с методом Ньютона, но имеет немного меньшую скорость сходимости. Порядок сходимости метода равен золотому сечению — 1,618…

Замечания. 1) Для начала итерационного процесса требуются два различных значения ${\displaystyle x_{0}}$ и ${\displaystyle x_{1}}$ .
2) В отличие от «настоящего метода Ньютона» (метода касательных), требующего хранить только ${\displaystyle x_{n}}$ (и в ходе вычислений — временно ${\displaystyle f(x_{n})}$ и ${\displaystyle f'(x_{n})}$), для метода секущих требуется сохранение ${\displaystyle x_{n-1}}$ , ${\displaystyle x_{n}}$ , ${\displaystyle f(x_{n-1})}$ , ${\displaystyle f(x_{n})}$ .
3) Применяется, если вычисление ${\displaystyle f'(x)}$ затруднено (например, требует большого количества машинных ресурсов: времени и/или памяти).

Метод одной касательной[править | править код]

В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.

Формула итераций этого метода имеет вид:

${\displaystyle x_{n+1}=x_{n}-{\frac {1}{f'(x_{0})}}f(x_{n}).}$

Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения ${\displaystyle x_{0}}$, а затем использовать это значение на каждой последующей итерации:

${\displaystyle \alpha (x)=\alpha _{0}=-{\dfrac {1}{f'(x_{0})}}.}$

При таком выборе ${\displaystyle \alpha _{0}}$ в точке ${\displaystyle x_{0}}$ выполнено равенство:

${\displaystyle \varphi '(x_{0})=1+\alpha _{0}f'(x_{0})=0,}$

и если отрезок, на котором предполагается наличие корня ${\displaystyle x^{*}}$ и выбрано начальное приближение ${\displaystyle x_{0}}$, достаточно мал, а производная ${\displaystyle \varphi '(x)}$ непрерывна, то значение ${\displaystyle \varphi '(x^{*})}$ будет не сильно отличаться от ${\displaystyle \varphi '(x_{0})=0}$ и, следовательно, график ${\displaystyle y=\varphi (x)}$ пройдёт почти горизонтально, пересекая прямую ${\displaystyle y=x}$, что в свою очередь обеспечит быструю сходимость последовательности точек приближений к корню.

Этот метод является частным случаем метода простой итерации. Он имеет линейный порядок сходимости.

Метод Ньютона-Фурье[править | править код]

Метод Ньютона-Фурье - это расширение метода Ньютона, выведенное Жозефом Фурье для получения оценок на абсолютную ошибку аппроксимации корня, в то же время обеспечивая квадратичную сходимость с обеих сторон.

Предположим, что f(x) дважды непрерывно дифференцируема на отрезке [a, b] и что f имеет корень на этом интервале. Дополнительно положим, что f′(x), f″(x) ≠ 0 на этом отрезке (например, это верно, если f(a) < 0, f(b) > 0, и f″(x) > 0 на этом отрезке). Это гарантирует наличие единственного корня на этом отрезке, обозначим его α. Эти рассуждения относятся к вогнутой вверх функции. Если она вогнута вниз, то заменим f(x) на −f(x), поскольку они имеют одни и те же корни.

Пусть x₀ = b будет правым концом отрезка, на котором мы ищем корень, а z₀ = a - левым концом того же отрезка. Если x_n найдено, определим

${\displaystyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}},}$

которое выражает обычный метод Ньютона, как описано выше. Затем определим

${\displaystyle z_{n+1}=z_{n}-{\frac {f(z_{n})}{f'(x_{n})}},}$

где знаменатель равен f′(x_n), а не f′(z_n). Итерации x_n будут строго убывающими к корню, а итерации z_n - строго возрастающими к корню. Также выполняется следующее соотношение:

${\displaystyle \lim _{n\to \infty }{\frac {x_{n+1}-z_{n+1}}{(x_{n}-z_{n})^{2}}}={\frac {f''(\alpha )}{2f'(\alpha )}}}$,

таким образом, расстояние между x_n и z_n уменьшается квадратичным образом.

Многомерный случай[править | править код]

Обобщим полученный результат на многомерный случай.

Пусть необходимо найти решение системы:

${\displaystyle \left\{{\begin{array}{lcr}f_{1}(x_{1},\;x_{2},\;\ldots ,\;x_{n})&=&0,\\\ldots &&\\f_{m}(x_{1},\;x_{2},\;\ldots ,\;x_{n})&=&0.\end{array}}\right.}$

Выбирая некоторое начальное значение ${\displaystyle {\vec {x}}^{[0]}}$, последовательные приближения ${\displaystyle {\vec {x}}^{[j+1]}}$ находят путём решения систем уравнений:

${\displaystyle f_{i}+\sum _{k=1}^{n}{\frac {\partial f_{i}}{\partial x_{k}}}(x_{k}^{[j+1]}-x_{k}^{[j]})=0,\qquad i=1,\;2,\;\ldots ,\;m,}$

где ${\displaystyle {\vec {x}}^{[j]}=(x_{1}^{[j]},\;x_{2}^{[j]},\;\ldots ,\;x_{n}^{[j]}),\quad j=0,\;1,\;2,\;\ldots }$.

Применительно к задачам оптимизации[править | править код]

Пусть необходимо найти минимум функции многих переменных ${\displaystyle f({\vec {x}})\colon \mathbb {R} ^{n}\to \mathbb {R} }$. Эта задача равносильна задаче нахождения нуля градиента ${\displaystyle \nabla f({\vec {x}})}$. Применим изложенный выше метод Ньютона:

${\displaystyle \nabla f({\vec {x}}^{[j]})+H({\vec {x}}^{[j]})({\vec {x}}^{[j+1]}-{\vec {x}}^{[j]})=0,\quad j=1,\;2,\;\ldots ,\;n,}$

где ${\displaystyle H({\vec {x}})}$ — гессиан функции ${\displaystyle f({\vec {x}})}$.

В более удобном итеративном виде это выражение выглядит так:

${\displaystyle {\vec {x}}^{[j+1]}={\vec {x}}^{[j]}-H^{-1}({\vec {x}}^{[j]})\nabla f({\vec {x}}^{[j]}).}$

В случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.

Нахождение матрицы Гессе связано с большими вычислительными затратами, и зачастую не представляется возможным. В таких случаях альтернативой могут служить квазиньютоновские методы, в которых приближение матрицы Гессе строится в процессе накопления информации о кривизне функции.

Метод Ньютона — Рафсона[править | править код]

Метод Ньютона — Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:

${\displaystyle {\vec {x}}^{[j+1]}={\vec {x}}^{[j]}-\lambda _{j}H^{-1}({\vec {x}}^{[j]})\nabla f({\vec {x}}^{[j]}),}$

где ${\displaystyle \lambda _{j}=\arg \min _{\lambda }f({\vec {x}}^{[j]}-\lambda H^{-1}({\vec {x}}^{[j]})\nabla f({\vec {x}}^{[j]})).}$ Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением ${\displaystyle H(f({\vec {x}}^{[0]}))}$ и обновляют его лишь раз в ${\displaystyle m}$ шагов, либо не обновляют вовсе.

Применительно к задачам о наименьших квадратах[править | править код]

На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:

${\displaystyle F({\vec {x}})=\|{\vec {f}}({\vec {x}})\|=\sum _{i=1}^{m}f_{i}^{2}({\vec {x}})=\sum _{i=1}^{m}(\varphi _{i}({\vec {x}})-{\mathcal {F}}_{i})^{2}\to \min .}$

Эти задачи отличаются особым видом градиента и матрицы Гессе:

${\displaystyle \nabla F({\vec {x}})=2J^{T}({\vec {x}}){\vec {f}}({\vec {x}}),}$

${\displaystyle H({\vec {x}})=2J^{T}({\vec {x}})J({\vec {x}})+2Q({\vec {x}}),\qquad Q({\vec {x}})=\sum _{i=1}^{m}f_{i}({\vec {x}})H_{i}({\vec {x}}),}$

где ${\displaystyle J({\vec {x}})}$ — матрица Якоби вектор-функции ${\displaystyle {\vec {f}}({\vec {x}})}$, ${\displaystyle H_{i}({\vec {x}})}$ — матрица Гессе для её компоненты ${\displaystyle f_{i}({\vec {x}})}$.

Тогда очередной шаг ${\displaystyle {\vec {p}}}$ определяется из системы:

${\displaystyle \left[J^{T}({\vec {x}})J({\vec {x}})+\sum _{i=1}^{m}f_{i}({\vec {x}})H_{i}({\vec {x}})\right]{\vec {p}}=-J^{T}({\vec {x}}){\vec {f}}({\vec {x}}).}$

Метод Гаусса — Ньютона[править | править код]

Метод Гаусса — Ньютона строится на предположении о том, что слагаемое ${\displaystyle J^{T}({\vec {x}})J({\vec {x}})}$ доминирует над ${\displaystyle Q({\vec {x}})}$. Это требование не соблюдается, если минимальные невязки велики, то есть если норма ${\displaystyle \|{\vec {f}}({\vec {x}})\|}$ сравнима с максимальным собственным значением матрицы ${\displaystyle J^{T}({\vec {x}})J({\vec {x}})}$. В противном случае можно записать:

${\displaystyle J^{T}({\vec {x}})J({\vec {x}}){\vec {p}}=-J^{T}({\vec {x}}){\vec {f}}({\vec {x}}).}$

Таким образом, когда норма ${\displaystyle \|Q({\vec {x}})\|}$ близка к нулю, а матрица ${\displaystyle J({\vec {x}})}$ имеет полный столбцевой ранг, шаг ${\displaystyle {\vec {p}}}$ мало отличается от ньютоновского (с учётом ${\displaystyle Q({\vec {x}})}$), и метод может достигать квадратичной скорости сходимости, хотя вторые производные и не учитываются. Улучшением метода является алгоритм Левенберга — Марквардта, основанный на эвристических соображениях.

Обобщение на комплексную плоскость[править | править код]

До сих пор в описании метода использовались функции, осуществляющие отображения в пределах множества вещественных значений. Однако метод может быть применён и для нахождения нуля функции комплексной переменной. При этом процедура остаётся неизменной:

${\displaystyle z_{n+1}=z_{n}-{\frac {f(z_{n})}{f'(z_{n})}}.}$

Особый интерес представляет выбор начального приближения ${\displaystyle z_{0}}$. Ввиду того, что функция может иметь несколько нулей, в различных случаях метод может сходиться к различным значениям, и вполне естественно возникает желание выяснить, какие области обеспечат сходимость к тому или иному корню. Этот вопрос заинтересовал Артура Кэли ещё в 1879 году, однако разрешить его смогли лишь в 70-х годах двадцатого столетия с появлением вычислительной техники. Оказалось, что на пересечениях этих областей (их принято называть областями притяжения) образуются так называемые фракталы — бесконечные самоподобные геометрические фигуры.

Ввиду того, что Ньютон применял свой метод исключительно к полиномам, фракталы, образованные в результате такого применения, обрели название фракталов Ньютона или бассейнов Ньютона.

Реализация[править | править код]

Scala[править | править код]

object NewtonMethod {    val accuracy = 1e-6    @tailrec   def method(x0: Double, f: Double => Double, dfdx: Double => Double, e: Double): Double = {     val x1 = x0 - f(x0) / dfdx(x0)     if (abs(x1 - x0) < e) x1     else method(x1, f, dfdx, e)   }    def g(C: Double) = (x: Double) => x*x - C    def dgdx(x: Double) = 2*x    def sqrt(x: Double) = x match {     case 0 => 0     case x if (x < 0) => Double.NaN     case x if (x > 0) => method(x/2, g(x), dgdx, accuracy)    } } 

Python[править | править код]

from math import sin, cos from typing import Callable import unittest   def newton(f: Callable[[float], float], f_prime: Callable[[float], float], x0: float,  	eps: float=1e-7, kmax: int=1e3) -> float: 	""" 	solves f(x) = 0 by Newton's method with precision eps 	:param f: f 	:param f_prime: f' 	:param x0: starting point 	:param eps: precision wanted 	:return: root of f(x) = 0 	""" 	x, x_prev, i = x0, x0 + 2 * eps, 0 	 	while abs(x - x_prev) >= eps and i < kmax: 		x, x_prev, i = x - f(x) / f_prime(x), x, i + 1  	return x   class TestNewton(unittest.TestCase): 	def test_0(self): 		def f(x: float) -> float: 			return x**2 - 20 * sin(x)   		def f_prime(x: float) -> float: 			return 2 * x - 20 * cos(x)   		x0, x_star = 2, 2.7529466338187049383  		self.assertAlmostEqual(newton(f, f_prime, x0), x_star)   if __name__ == '__main__': 	unittest.main() 

PHP[править | править код]

<?php // PHP 5.4 function newtons_method( 	$a = -1, $b = 1,  	$f = function($x) { 	 		return pow($x, 4) - 1; 	 	}, 	$derivative_f = function($x) {  		return 4 * pow($x, 3); 	 	}, $eps = 1E-3) {          $xa = $a;         $xb = $b;          $iteration = 0;          while (abs($xb) > $eps) {              $p1 = $f($xa);             $q1 = $derivative_f($xa);             $xa -= $p1 / $q1;             $xb = $p1;             ++$iteration;          }          return $xa;  } 

Octave[править | править код]

function res = nt()   eps = 1e-7;   x0_1 = [-0.5,0.5];   max_iter = 500;   xopt = new(@resh, eps, max_iter);      xopt endfunction function a = new(f, eps, max_iter)   x=-1;   p0=1;   i=0;  while (abs(p0)>=eps)     [p1,q1]=f(x);     x=x-p1/q1;    p0=p1;    i=i+1;  end  i  a=x; endfunction function[p,q]= resh(x)   % p= -5*x.^5+4*x.^4-12*x.^3+11*x.^2-2*x+1;    p=-25*x.^4+16*x.^3-36*x.^2+22*x-2;    q=-100*x.^3+48*x.^2-72*x+22; endfunction 

Delphi[править | править код]

// вычисляемая функция function fx(x: Double): Double; begin   Result := x * x - 17; end;  // производная функция от f(x) function dfx(x: Double): Double; begin   Result := 2 * x; end;  function solve(fx, dfx: TFunc<Double, Double>; x0: Double): Double; const   eps = 0.000001; var   x1: Double; begin   x1 := x0 - fx(x0) / dfx(x0); // первое приближение   while (Abs(x1-x0) > eps) do begin // пока не достигнута точность 0.000001     x0 := x1;     x1 := x1 - fx(x1) / dfx(x1); // последующие приближения   end;   Result := x1; end;  // Вызов solve(fx, dfx,4)); 

C++[править | править код]

#include <stdio.h> #include <math.h>  #define eps 0.000001 double fx(double x) { return x * x - 17;} // вычисляемая функция double dfx(double x) { return 2 * x;} // производная функции  typedef double(*function)(double x); // задание типа function  double solve(function fx, function dfx, double x0) {   double x1  = x0 - fx(x0) / dfx(x0); // первое приближение   while (fabs(x1 - x0) > eps) { // пока не достигнута точность 0.000001     x0 = x1;     x1 = x0 - fx(x0) / dfx(x0); // последующие приближения   }   return x1; }  int main () {   printf("%f\n", solve(fx, dfx, 4)); // вывод на экран   return 0; } 

C[править | править код]

typedef double (*function)(double x);  double TangentsMethod(function f, function df, double xn, double eps) {    double x1  = xn - f(xn)/df(xn);    double x0 = xn;    while(abs(x0-x1) > eps) {       x0 = x1;       x1 = x1 - f(x1)/df(x1);    }    return x1; }  //Выбор начального приближения xn = MyFunction(A)*My2Derivative(A) > 0 ? B : A;  double MyFunction(double x) { return (pow(x, 5) - x - 0.2); } //Ваша функция double MyDerivative(double x) { return (5*pow(x, 4) - 1); } //Первая производная double My2Derivative(double x) { return (20*pow(x, 3)); } //Вторая производная  //Пример вызова функции double x = TangentsMethod(MyFunction, MyDerivative, xn, 0.1) 

Haskell[править | править код]

import Data.List ( iterate' )  main :: IO () main = print $ solve (\ x -> x * x - 17) ( * 2) 4  -- Функция solve универсальна для всех вещественных типов значения которых можно сравнивать. solve = esolve 0.000001  esolve epsilon func deriv x0 = fst . head $ dropWhile pred pairs   where     pred (xn, xn1) = (abs $ xn - xn1) > epsilon -- Функция pred определяет достигнута ли необходимая точность.     next xn = xn - func xn / deriv xn -- Функция next вычисляет новое приближение.     iters   = iterate' next x0        -- Бесконечный список итераций.     pairs   = zip iters (tail iters)  -- Бесконечный список пар итераций вида: [(x0, x1), (x1, x2) ..].