Pi – Wikipédia, a enciclopédia livre

 Nota: Este artigo é sobre a constante matemática. Para letra graga, veja Π. Para o estado brasileiro, veja Piauí. Para outros significados, veja PI.

Parte de uma série de artigos sobre:
a constante matemática π
3.1415926535897932384626433...
Utilização
Área do círculo Circunferência Uso em outras fórmulas
Propriedades
Irracionalidade Transcendência
Valor
Menor que 22/7 Aproximações Memorização
Pessoas
Arquimedes Liu Hui Tsu Ch'ung Chih Ariabata Madhava Alcaxi Ludolph van Ceulen François Viète Seki Takakazu William Jones John Machin William Shanks Srinivāsa Rāmānujan John Wrench Yasumasa Kanada
História
Cronologia Livro
Na cultura
Projeto de lei de Indiana Dia do Pi
Tópicos relacionados
Quadratura do círculo Problema de Basileia Seis noves em pi
v d e

O número π (pronuncia-se [pi]) é uma constante matemática que é razão entre o comprimento de uma circunferência e seu diâmetro, aproximadamente igual a 3,14159. O número π aparece em diversas fórmulas matemáticas e físicas. É um número irracional, que significa que não pode ser expresso como a razão de dois inteiros, por mais que frações como ${\displaystyle {\tfrac {22}{7}}}$ são comumente utilizadas para ter um valor aproximado. Consequentemente, sua representação decimal nunca acaba, nem entra num padrão que se repete permanentemente. Também é um número transcendente, ou seja, não é a solução de uma equação envolva apenas infinitas somas, produtos, potências, e inteiros. Este último fato implica que resolver o antigo problema da quadratura do círculo com régua e compasso é impossível. Os dígitos decimais de π são aparentemente distribuídos aleatoriamente,^[a] mas nenhuma prova para essa conjetura foi encontrada.

Por milhares de anos, matemáticos tentaram expandir seus conhecimentos sobre π, às vezes computando o seu valor a um alto nível de acuracidade. Civilizações antigas, incluindo os egípcios e os babilônicos, exigiam aproximações bastante precisas de π para cálculos práticos. Aproximadamente 250 a.C., o matemático grego Archimedes criou um algoritmo para aproximar π com uma precisão arbitrária. No século V d.C., matemáticos chineses aproximaram π a sete dígitos, enquanto os matemáticos indianos fizeram uma aproximação de cinco dígitos, ambos utilizando técnicas geométricas. A primeira fórmula computacional, baseado numa série infinita, foi descoberta um milênio depois.^[1][2] O primeiro uso da letra π para representar a razão entre o comprimento da circunferência e o seu diâmetro foi o matemático galês William Jones em 1706.^[3]

A invenção do cálculo logo levou à computação de centenas de dígitos de π, o suficiente para todas as computações científicas práticas. No entanto, nos séculos XX e XXI, matemáticos e cientistas da computação buscaram novas abordagens que, combinadas com o aumento da potência computacional, estenderam a representação decimal de π para muitos trilhões de dígitos.^[4][5] Essas computações são motivados pelo desenvolvimento de algoritmos eficientes para calcular séries numéricas, bem como pela busca humana por quebrar recordes.^[6][7] Os extensos cálculos envolvidos também foram usados para testar supercomputadores, bem como para testar o hardware de computadores de consumidores.

Pela sua definição estar relacionada à circunferência, π é encontrado em muitas fórmulas de trigonometria e geometria, especialmente aquelas relacionadas a circunferências, elipses e esferas. A constante pode ser encontrada também em fórmulas de outros tópicos da ciência, como cosmologia, fractais, termodinâmica, mecânica e eletromagnetismo. Também aparece em áreas pouco relacionadas à geometria, como teoria dos números e estatística, e na análise matemática moderna pode ser definido sem qualquer referência à geometria. A ubiquidade de π faz com que seja uma das constantes matemáticas mais amplamente conhecidas dentro e fora da ciência. Vários livros dedicados a π foram publicados, e cálculos de recorde dos dígitos de π frequentemente resultam em manchetes de notícias.

Fundamentos[editar | editar código-fonte]

Nome[editar | editar código-fonte]

O símbolo utilizado pelos matemáticos para representar a razão entre o comprimento de uma circunferência pelo seu diâmetro é a letra grega π minúscula, às vezes escrito como pi.^[8] Em português, π é pronunciado como [pi].^[9] Em usos matemáticos, a letra π minúscula é diferenciada de sua forma maiúscula Π, utilizado para denotar o produtório, análogo a como Σ é utilizado para denotar o somatório.

A escolha do símbolo π é discutia na seção Adoção do símbolo π.

Definição[editar | editar código-fonte]

π é comumente definido como a razão do comprimento de uma circunferência C pelo seu diâmetro d:^[10]

$${\displaystyle \pi ={\frac {C}{d}}}$$

A razão ${\textstyle {\frac {C}{d}}}$ é constante, independente do tamanho da circunferência. Por exemplo, se uma circunferência possui o dobro do diâmetro de outra circunferência, o seu comprimento também será o dobro, preservando a razão mencionada. Esta definição de π implica o uso de geometria (euclidiana) plana; por mais que a noção de circunferência pode ser estendida para qualquer geometria (não euclidiana) curva, esse não satisfazem a fórmula ${\textstyle \pi ={\frac {C}{d}}}$.^[10]

Aqui, o comprimento de uma circunferência é o comprimento do arco ao redor do perímetro da circunferência, uma quantidade que pode ser formalmente definida independentemente da geometria utilizando limites — um conceito do cálculo.^[11] Por exemplo, pode-se calcular diretamente o comprimento do arco da metade superior da circunferência unitária, dado em coordenadas cartesianas pela equação x² + y² = 1, como a integral:^[12]

$${\displaystyle \pi =\int _{-1}^{1}{\frac {dx}{\sqrt {1-x^{2}}}}.}$$

Uma integral como essa foi adotada como a definição para π por Karl Weierstrass, quem a definiu diretamente como uma integral em 1841.^[b]

Integração não é mais usualmente utilizado para a primeira definição analítica, porque, conforme Remmert explica, cálculo diferencial precede tipicamente o cálculo integral nos currículos das universidades, então é desejado uma definição para π que não necessite utilizar integrais.^[12] Uma dessas definições, de Richard Baltzer^[13] e popularizado por Edmund Landau,^[14] é a seguinte: π é o dobro do menor número positivo no qual seu cosseno é igual a 0.^[10][12][15] π também é o menor número positivo no qual o seno é igual a zero, e a diferença entre duas raízes consecutivas da função seno e cosseno. O cosseno e o seno podem ser definidos independentemente da geometria, como uma série de potências^[16] ou a solução de uma equação diferencial.^[15]

Semelhantemente, π pode ser definido utilizando as propriedades das função exponencial complexa exp z, de uma variável complexa z. Como o cosseno, a função exponencial complexa pode ser definida de diversas maneiras diferentes. O conjunto de números complexos no qual exp z é igual a um é então uma progressão aritmética (imaginária) da forma:

$${\displaystyle \{\dots ,-2\pi i,0,2\pi i,4\pi i,\dots \}=\{2\pi ki\mid k\in \mathbb {Z} \}}$$

e há um único número real positivo π com essa propriedade.^[17][18]

Uma variação da mesma, utilizando conceitos matemáticos sofisticados de topologia e álgebra, é o seguinte teorema:^[19] há um único (Salvo por automorfismo) isomorfismo contínuo do grupo R/Z de números reais sob a adição módulo inteiro (o grupo circular), no grupo multiplicativo de números complexos de valor absoluto um. O número π é definido como metade da magnitude da derivada deste homomorfismo.^[20]

Irracionalidade e normalidade[editar | editar código-fonte]

π é um número irracional, o que significa que não pode ser escrito como uma razão de dois números inteiros. Frações como 227 e 355113 são usualmente utilizadas para aproximar π, mas nenhuma fração comum (razão entre dois números inteiros) pode expressar seu exato valor.^[21] Visto que π é irracional, ele possui um infinito número de dígitos em sua representação decimal, nem é uma dízima periódica. Há diversas provas da irracionalidade de π; elas geralmente requerem cálculo e utilizam a técnica de redução ao absurdo. O grau no qual π pode ser aproximado por números racionais (chamado de medida de irracionalidade) não é precisamente conhecido; é estimado que seja maior que a medida de e ou ln 2, mas menor que a medida dos números de Liouville.^[22]

Os dígitos de π não aparentam possuir nenhum tipo de padrão, passando em testes de aleatoriedade estatística, incluindo o teste de normalidade; um número de comprimento infinito é dito normal quando em todas as sequências de dígitos (de comprimento qualquer) aparecem com a mesma frequência. A conjectura de que π seja normal não foi provada nem refutada.^[23]

Desde a chegada dos computadores, inúmeros dígitos estiveram disponíveis para realizar análise estatística. Yasumasa Kanada realizou uma análise estatística detalhada nos dígitos decimais de π, encontrando consistência na normalidade; por exemplo, a frequência dos dígitos de 0 a 9 foram submetidos a testes de significância estatística, e nenhum padrão foi encontrado.^[24] Qualquer sequência aleatória de dígitos contém subsequências de comprimento arbitrário que parecem não aleatórios, pelo teorema do macaco infinito. Portanto, porque a sequência de dígitos de π passa em testes estatísticos de aleatoriedade, ele contém algumas sequências de dígitos que aparentam não ser aleatórias, como a sequência de seis noves consecutivos que começa na 762.ª casa decimal da representação decimal de π.^[25] Isto também é conhecido como o "ponto de Freynman" no "folclore matemático", em homenagem a Richard Feynman, porém não há nenhuma ligação conhecida com Feynman.

Transcendência[editar | editar código-fonte]

Em adição de ser irracional, π também é um número transcendente, o que significa que não é a solução de nenhuma equação polinomial não constante com coeficientes racionais, como ${\textstyle {\frac {x^{5}}{120}}-{\frac {x^{3}}{6}}+x=0}$.^[26][c]

A transcendência de π tem duas importantes consequências: a primeira é que π não pode ser expresso utilizando uma combinação finita de raízes quadradas ou raízes n-ésimas (como ${\displaystyle {\sqrt[{3}]{31}}}$ ou ${\displaystyle {\sqrt {10}}}$). A segunda é que, como não é possível construir [en] números transcendentes com régua e compasso, a quadratura do círculo é impossível. Noutras palavras, é impossível construir, utilizando apenas régua e compasso, um quadrado cuja área é exatamente igual à área de um dado círculo.^[27] A quadratura do círculo era um dos importantes problemas da Antiguidade Clássica.^[28] Matemáticos amadores da modernidade às vezes tentam quadrar o círculo e reivindicam sucesso — mesmo sendo de fato algo matematicamente impossível.^[29][30]

Frações contínuas[editar | editar código-fonte]

Como é irracional, π não pode ser representado como uma fração comum. Mas todo número, incluindo π, pode ser representado como uma série infinita de frações uma dentro da outra, chamada de fração contínua:

$${\displaystyle \pi =3+\textstyle {\cfrac {1}{7+\textstyle {\cfrac {1}{15+\textstyle {\cfrac {1}{1+\textstyle {\cfrac {1}{292+\textstyle {\cfrac {1}{1+\textstyle {\cfrac {1}{1+\textstyle {\cfrac {1}{1+\ddots }}}}}}}}}}}}}}}$$

Truncando a fração contínua em qualquer ponto produz uma aproximação racional para π; as quatro primeiro são 3, 227, 333106, e 355113. Estes números estão entre as aproximações históricas mais conhecidas e mais amplamente utilizadas da constante. Cada aproximação gerada desta forma se aproxima cada vez mais de π; ou seja, cada fração é mais próxima de π que uma de denominador igual ou menor.^[31] Visto que π é transcendente, por definição não é algébrico e não pode ser um irracional quadrático. Portanto, não há uma fração contínua periódica para π. Por mais que fração contínua simples (mostrada acima) não demonstra nenhum padrão óbvio,^[32][33] diversas frações contínuas generalizadas apresentam, como, por exemplo:^[34]

$${\displaystyle {\begin{aligned}\pi &=3+{\cfrac {1^{2}}{6+{\cfrac {3^{2}}{6+{\cfrac {5^{2}}{6+{\cfrac {7^{2}}{6+\ddots }}}}}}}}={\cfrac {4}{1+{\cfrac {1^{2}}{2+{\cfrac {3^{2}}{2+{\cfrac {5^{2}}{2+\ddots }}}}}}}}={\cfrac {4}{1+{\cfrac {1^{2}}{3+{\cfrac {2^{2}}{5+{\cfrac {3^{2}}{7+\ddots }}}}}}}}\end{aligned}}}$$

A fração do meio dessas se deve ao matemático de meados do século XVII William Brouncker, veja § Fórmula de Brouncker.

Valores aproximados e dígitos[editar | editar código-fonte]

Algumas Aproximações de pi incluem:

• Inteiros: 3
• Frações: Frações aproximadas incluem (em ordem crescente de acurácia) 227, 333106, 355113, 5216316604, 10399333102, 10434833215, e 24585092278256779.^[31] (Lista são termos selecionados de OEIS: A063674 e OEIS: A063673.)
• Dígitos: Os primeiros 50 dígitos decimais são 3,14159265358979323846264338327950288419716939937510...^[35] (ver OEIS: A000796)

Dígitos noutras bases

• Os primeiros 48 dígitos binários (base 2, chamado de bits) são 11.001001000011111101101010100010001000010110100011... (ver OEIS: A004601)
• Os primeiros 38 dígitos em ternário (base 3) são 10,0102110122220102110021111102212222201... (ver OEIS: A004602)
• Os primeiros 20 dígitos em hexadecimal (base 16) são 3,243F6A8885A308D31319...^[36] (ver OEIS: A062964)
• Os primeiros 5 dígitos em sexagesimal (base 60) são 3;8,29,44,0,47^[37] (ver OEIS: A060707)

Números complexos e identidade de Euler[editar | editar código-fonte]

Qualquer número complexo, consideremos z pode ser expresso utilizando um par de números reais. No sistema de coordenadas polares, um número (raio ou r) é utilizado para representar a distância de z da origem do plano complexo, e o outro (ângulo ou φ) é a rotação do eixo dos positivos reais:^[38]

$${\displaystyle z=r\cdot (\cos \varphi +i\sin \varphi ),}$$

onde i é a unidade imaginária que satisfaz i² = -1. A frequente aparição de π na análise complexa pode ser relacionada ao comportamento da função exponencial de uma variável complexa, descrita pela fórmula de Euler

$${\displaystyle e^{i\varphi }=\cos \varphi +i\sin \varphi ,}$$

onde e é a base do logaritmo natural. Esta fórmula estabelece uma correspondência entre as potências imaginárias de e e pontos no círculo unitário centrado na origem do plano complexo. Quando φ = π, o resultado é a identidade de Euler, considerado uma beleza da matemática por mostrar uma profunda conexão entre cinco importantes constantes matemáticas:^[39][40]

$${\displaystyle e^{i\pi }+1=0.}$$

Existem n diferentes números complexos z que satisfaçam zⁿ = 1, sendo chamadas de raízes n-ésimas da unidade,^[41] dadas pela fórmula:

$${\displaystyle e^{2\pi ik/n}\qquad (k=0,1,2,\dots ,n-1).}$$

Métodos de cálculo[editar | editar código-fonte]

Existem muitas formas de se obter o valor aproximado de ${\displaystyle \pi }$ através de métodos numéricos. Consideramos que ${\displaystyle \pi }$ é um número irracional e transcendente, de forma que os métodos de cálculo sempre envolvem aproximações, aproximações sucessivas e/ou séries infinitas de somas, multiplicações e divisões.

Método clássico[editar | editar código-fonte]

A primeira tentativa rigorosa de encontrar ${\displaystyle \pi }$ deve-se a um dos mais conhecidos matemáticos da antiguidade, Arquimedes. Pela construção de polígonos inscrito e circunscrito de 96 lados, encontrou que pi seria um valor entre 223/71 e 22/7, ou seja, estaria aproximadamente entre 3,1408 e 3,1429. Tal método é o chamado método clássico para cálculo de pi.^[42]

Ptolomeu, que viveu em Alexandria aproximadamente no século III d.C., calculou pi tomando por base um polígono de 720 lados inscrito numa circunferência de 60 unidades de raio. Seu valor foi aproximadamente 3,1416. Considerando o que sabemos atualmente, sua aproximação foi bem melhor que a de Arquimedes.

A busca pelo valor de ${\displaystyle {\pi }}$ chegou à China, onde Liu Hui, um copiador de livros, conseguiu obter o valor 3,14159 com um polígono de 3 072 lados. Mas só no final do século V que o matemático Tsu Ch'ung Chih chegou a uma aproximação melhor: entre 3,1415926 e 3,1415927.

Nesta mesma época, o matemático hindu Aryabhata deixou registrado em versos num livro a seguinte afirmação: "Some-se 4 a 100, multiplique-se por 8 e some-se 62 000. O resultado é aproximadamente uma circunferência de diâmetro 20 000".

Analisando matematicamente e considerando a equação citada anteriormente de ${\displaystyle c=\pi \cdot d:}$

${\displaystyle (4+100)\cdot 8+62000\approx \pi \cdot 20000\Rightarrow }$

${\displaystyle 104\cdot 8+62000\approx \pi \cdot 20000\Rightarrow }$

${\displaystyle 832+62000\approx \pi \cdot 20000\Rightarrow }$

${\displaystyle 62832\approx \pi \cdot 20000\Rightarrow }$

${\displaystyle {62832 \over 20000}\approx \pi }$

O valor de ${\displaystyle {\pi },}$ portanto, seria 3,1416. Obviamente, quanto maior o número de casas decimais, melhor a aproximação do valor real de pi. Mas devemos considerar que, na época, isso não era algo fácil de se calcular.

O maior cálculo de casas decimais até o século XV foi 3,1415926535897932 feito pelo matemático árabe Ghiyath al-Kashi. O matemático holandês Ludolph van Ceulen, no final do século XVI, calculou um valor de ${\displaystyle {\pi }}$ com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados. Por curiosidade, a sua esposa mandou gravar no seu túmulo o valor de ${\displaystyle {\pi }}$com as supracitadas 35 casas decimais.

Hoje em dia é relativamente mais fácil, com os computadores modernos que calculam até trilhões de casas decimais para ${\displaystyle {\pi }.}$

Uma aproximação de ${\displaystyle {\pi }}$ que apresenta diferença de aproximadamente ${\displaystyle 2{\text{,}}7\times 10^{-7}}$ é a seguinte:

${\displaystyle {355 \over 113}\approx \pi }$

Método de Arquimedes[editar | editar código-fonte]

Baseado no método de Arquimedes é possível formular uma representação matemática para o cálculo de pi, eficiente para um polígono de qualquer número de lados.

Considerando um polígono de n lados e raio 1, temos a medida do lado expressa pela lei dos cossenos:

${\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos \alpha }$

Temos formado um triângulo isósceles, de base ${\displaystyle l}$ e lados ${\displaystyle r=1}$:

${\displaystyle l^{2}=r^{2}+r^{2}-2r^{2}\cos \alpha }$

${\displaystyle l^{2}=1^{2}+1^{2}-2\cos \alpha }$

${\displaystyle l^{2}=2-2\cos \alpha }$

${\displaystyle l={\sqrt {2-2\cos \alpha }}}$

O ângulo do triângulo isósceles no centro do polígono é expresso por 360º dividido pelo número de lados ${\displaystyle n}$, portanto:

${\displaystyle l={\sqrt {2-2\cos \left({\frac {360}{n}}\right)}}}$

Dessa forma, o perímetro do polígono será de:

${\displaystyle p=n.{\sqrt {2-2\cos \left({\frac {360}{n}}\right)}}}$

Como ${\displaystyle \pi }$ é representado pelo perímetro do polígono dividido pelo seu diâmetro, temos:

${\displaystyle \pi ={\frac {n.{\sqrt {2-2\cos \left({\frac {360}{n}}\right)}}}{2}}}$

Aplicando transformações trigonométricas, a fórmula acima pode ser simplificada para:

${\displaystyle \pi =n.\operatorname {sen} \left({\frac {180}{n}}\right)}$

Métodos estatísticos[editar | editar código-fonte]

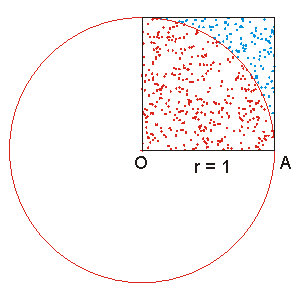
Outro método interessante para o cálculo de ${\displaystyle \pi }$ pode ser realizado através de Monte Carlo utilizando-se a estatística. Nesse método são sorteados aleatoriamente pontos num quadrado compreendido entre as coordenadas ${\displaystyle O=(0,0)}$ e ${\displaystyle B=(1,1).}$ Em seguida calcula-se a distância dos pontos sorteados ${\displaystyle c_{n}=(x_{n},y_{n})}$ até a origem ${\displaystyle O=(0,0)}$. ${\displaystyle \pi }$ pode ser aproximado através do número de pontos inscritos na circunferência de raio 1 em relação ao total de pontos sorteados no quadrado de lado 1.

No exemplo ao lado, ${\displaystyle \pi \cong 4\cdot 386/500=3,088}$.

Outro método que utiliza a estatística de Monte Carlo para o cálculo de ${\displaystyle \pi }$ é conhecido como Agulha de Buffon, proposto no século XVIII pelo naturalista francês Georges de Buffon.

Métodos de séries infinitas[editar | editar código-fonte]

O francês François Viète, estudando o método de Arquimedes, desenvolveu a seguinte série para o cálculo de ${\displaystyle \pi }$ em 1593:

${\displaystyle {\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdot \dots ={\frac {2}{\pi }}}$

O matemático John Wallis, desenvolveu outra série infinita em 1655:

${\displaystyle {\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdot \dots ={\frac {\pi }{2}}.}$

Outra série conhecida para o cálculo de ${\displaystyle \pi }$ foi desenvolvida por Leibniz em 1682, utilizando-se da série de Taylor para a função ${\displaystyle \arctan(x)}$, tomando-se ${\displaystyle x=1}$ e, por conseguinte, ${\displaystyle \arctan(1)={\frac {\pi }{4}}}$.

${\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-\dots ={\frac {\pi }{4}}.}$

Johann Heinrich Lambert publicou, em 1770, uma série na forma de divisões infinitas:

${\displaystyle {\frac {4}{\pi }}=1+{\frac {1^{2}}{3+{\frac {2^{2}}{5+{\frac {3^{2}}{7+{\frac {4^{2}}{9+{\frac {5^{2}}{11+{\frac {6^{2}}{\cdots }}}}}}}}}}}}}$

Métodos de cálculo numérico[editar | editar código-fonte]

Um dos estudos dos métodos de cálculo numérico é obter a raiz de uma função. Quando consideramos a função ${\displaystyle f(x)=\sin(x)}$ sabemos que ${\displaystyle f(\pi )=\sin(\pi )=0.}$ Os principais métodos do calculo numérico para a obtenção da raiz da função ${\displaystyle f(x)}$ podem incluir uma busca binária no intervalo ${\displaystyle [a,b]}$ onde se sabemos que ${\displaystyle f(3)=\sin(3)>0}$ ${\displaystyle (a=3)}$ e ${\displaystyle f(4)=\sin(4)<0}$ ${\displaystyle (b=4)}$ então podemos aprimorar o intervalo para:

${\displaystyle \left[a,{{a+b} \over 2}\right],}$ se ${\displaystyle f\left({{a+b} \over 2}\right)<0}$ e

${\displaystyle \left[{{a+b} \over 2},b\right],}$ se ${\displaystyle f\left({{a+b} \over 2}\right)\geq 0}$

Partindo-se do intervalo ${\displaystyle \pi \in [3,4]}$ esse método permite refiná-lo sucessivamente para os intervalos

1. ${\displaystyle \pi \in [3;3,5]}$
2. ${\displaystyle \pi \in [3;3,25]}$
3. ${\displaystyle \pi \in [3,125;3,25]}$
4. ${\displaystyle \pi \in [3,125;3,1875]}$

e assim sucessivamente.

Ainda no cálculo numérico, o método de Newton-Raphson, mais eficiente que uma busca binária permite obter aproximações sucessivas para a raiz da função ${\displaystyle f(x)=\sin(x)}$ utilizando um ponto inicial ${\displaystyle x_{0}}$ exigindo que conheçamos ${\displaystyle f'(x)=\cos(x).}$

Tomando-se ${\displaystyle x_{0}=3}$ e considerando-se que por Newton-Rapson

${\displaystyle x_{i+1}=x_{i}-{{f(x_{i})} \over {f'(x_{i})}}=x_{i}-{{\sin(x_{i})} \over {\cos(x_{i})}}=x_{i}-{\tan(x_{i})},}$

temos a seguinte série para ${\displaystyle \pi }$

1. ${\displaystyle x_{0}=3}$
2. ${\displaystyle x_{1}=3,14254654}$
3. ${\displaystyle x_{2}=3,14159265}$

Um método otimizado de cálculo numérico para o cálculo de ${\displaystyle \pi }$ através das raízes de uma função pode ser obtido pela simplificação

${\displaystyle x_{i+1}=x_{i}+\sin(x_{i}),}$

pois na proximidade de ${\displaystyle \pi ,}$ ${\displaystyle \cos(x_{i})\cong -1.}$^[43]

Notemos que nesses algoritmos de cálculo numérico considera-se ${\displaystyle \pi }$ como transcendental, uma vez que a função ${\displaystyle f(x)=\sin(x)}$ não pode ser escrita através de um polinômio finito de coeficientes racionais; a função ${\displaystyle f(x)=\sin(x)}$ é obtida através da expansão da série de Taylor.

Algoritmo de Gauss-Legendre[editar | editar código-fonte]

O algoritmo de Gauss-Legendre,^[44] que é um método de cálculo numérico de aproximações sucessivas,^[45] foi utilizado por Yasumasa Kanada para obter o recorde mundial no cálculo de casas decimais de pi em 2002.^[46]

Método de cálculo isolado das decimais ${\displaystyle {\pi }}$[editar | editar código-fonte]

Em 1995, David Harold Bailey, em colaboração com Peter Borwein e Simon Plouffe, descobriu uma fórmula de cálculo de ${\displaystyle {\pi }}$, uma soma infinita (frequentemente chamada fórmula BBP):

${\displaystyle \pi =\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {4}{8k+1}}-{\frac {2}{8k+4}}-{\frac {1}{8k+5}}-{\frac {1}{8k+6}}\right)}$

Essa fórmula permite calcular facilmente a enésima decimal binária ou hexadecimal de ${\displaystyle {\pi }}$sem ter que calcular as decimais precedentes. O sítio de Bailey contém sua derivação e implementação em diversas linguagens de programação. Graças a uma fórmula derivada da fórmula BBP, o 4 000 000 000 000 000° algarismo de ${\displaystyle \pi }$ em base 2 foi obtido em 2001.

Grandezas que dependem de π[editar | editar código-fonte]

Várias relações matemáticas dependem do conhecimento da constante ${\displaystyle \pi ,}$ as mais conhecidas a nível didático são:

• Perímetro de uma circunferência: ${\displaystyle C=2\cdot \pi \cdot r}$
• Área do círculo: ${\displaystyle A=\pi \cdot r^{2}}$
• Volume de uma esfera: ${\displaystyle V={4 \over 3}\cdot \pi \cdot r^{3}}$

Como a superfície da esfera é ${\displaystyle S=4\pi r^{2}}$, ${\displaystyle \pi }$ também está nas fórmulas gravitacionais e do eletromagnetismo da física ${\displaystyle \left(F={1 \over 4\cdot \pi \cdot \epsilon _{0}}\cdot {Q\cdot q \over d^{2}}\right)}$.

Irracionalidade e transcendência de π[editar | editar código-fonte]

Ver artigos principais: Prova da irracionalidade de π e teorema de Lindemann–Weierstrass

Johann Heinrich Lambert demonstrou em 1761 que se ${\displaystyle x}$ é racional e diferente de ${\displaystyle 0}$, então nem ${\displaystyle \tan(x)}$ nem ${\displaystyle e^{x}}$ podem ser racionais. Como ${\displaystyle \tan \left({\frac {\pi }{4}}\right)=1}$, segue-se que ${\displaystyle {\frac {\pi }{4}}}$ é irracional, e portanto que ${\displaystyle \pi }$ é irracional.^[47][48]

Lindemann provou em 1882 que ${\displaystyle \pi }$ é transcendente utilizando o método utilizado por Hermite para provar que e é transcendente. Isto significa que ${\displaystyle \pi }$ não pode ser a solução de nenhuma equação algébrica de coeficientes racionais. A transcendência de ${\displaystyle {\pi }}$ estabelece a impossibilidade de se resolver o problema da quadratura do círculo: é impossível construir, somente com régua e um compasso euclideanos, um quadrado cuja área seja rigorosamente igual à área de um determinado círculo.

Questões sem resposta[editar | editar código-fonte]

A questão em aberto mais importante é a de saber se ${\displaystyle {\pi }}$ é um número normal, isto é, se qualquer sucessão de algarismos aparece nas decimais de ${\displaystyle {\pi },}$ como seria de se esperar em uma sequência infinita e completamente aleatória de algarismos. Isso deveria ser verdadeiro em qualquer base, e não somente na base 10.

Também não se sabe que algarismos aparecem um número infinito de vezes na constituição de ${\displaystyle {\pi }.}$

Bailey e Crandall demonstraram em 2000 que a existência da fórmula Bailey-Borwein-Plouffe mencionada acima e de fórmulas similares implicam a normalidade de ${\displaystyle {\pi }}$ em base 2.

Cronologia do cálculo de π[editar | editar código-fonte]

Ver artigo principal: Cronologia do cálculo de pi

Na tabela a seguir encontram-se listadas distintas precisões alcançadas no cálculo do valor de pi, permitindo ver a evolução ao longo do período histórico.^[49]

Ver também[editar | editar código-fonte]

• Aproximações de π
• Cronologia do cálculo de pi

Notas

Referências

Bibliografia[editar | editar código-fonte]

Ligações externas[editar | editar código-fonte]

O Commons possui uma categoria com imagens e outros ficheiros sobre Pi

• Curiosidades da Matemática - Evolução cronológica do cálculo de pi
• pi to 10,000 digits - The University of Utah (em inglês)
• Pi, o mais notável símbolo matemático.

• Portal da matemática