Paridade do zero – Wikipédia, a enciclopédia livre

A expressão paridade do zero refere-se ao fato de o número zero ser considerado um número par. Em outras palavras, sua paridade — a qualidade de um número inteiro ser par ou ímpar — é par. A maneira mais simples de provar que zero é par é checar se ele se encaixa na definição de número par: é um número inteiro, múltiplo de 2, especificamente . Como resultado disso, zero compartilha todas as propriedades que caracterizam os números pares: 0 é divisível por 2, é avizinhado de ambos os lados por números ímpares, é obtido através da soma de um inteiro com ele mesmo () e um conjunto com 0 objetos pode ser separado em dois conjuntos de mesmo tamanho.
Zero também se encaixa nos padrões formados por outros números pares. As regras aritméticas de paridade, tais como , requerem que 0 seja par. Zero é o elemento neutro do grupo de inteiros pares, e é o caso inicial a partir do qual outros números naturais pares são recursivamente definidos. Aplicações dessa recursão, da teoria dos grafos até a geometria computacional, requerem a paridade de zero. Não somente 0 é divisível por 2, como também é divisível por toda potência de 2, o que é extremamente relevante para o sistema de numeração binário usado por computadores. Nesse sentido, 0 é o número "mais par" de todos.[1]
Entre o público geral, a paridade do zero pode ser uma fonte de confusão. Em experimentos psicológicos de tempo de reação, muitas pessoas são mais lentas em identificar 0 como par do que identificar a paridade de 2, 4, 6 ou 8, por exemplo. Alguns estudantes de matemática — e alguns professores — pensam que zero é ímpar, ou ambos (par e ímpar), ou nenhum dos dois. Pesquisadores em educação matemática dizem que esses equívocos podem se tornar oportunidades de aprendizado. Estudar igualdades como pode sanar dúvidas de estudantes sobre se 0 é um número e sobre usá-lo na aritmética. Discussões de classe podem levar estudantes a avaliar os princípios básicos do raciocínio matemático, tais como a importância das definições. Analisando a paridade desse número excepcional é um exemplo precoce de um tema que permeia a matemática: a abstração de um conceito familiar para uma configuração desconhecida mais complexa.
Por que zero é par[editar | editar código-fonte]
A definição mais difundida de "número par" pode ser usada para provar diretamente que zero é um número par. Um número é chamado "par" se for um inteiro múltiplo de 2. Como um exemplo, o motivo de 10 ser par é que ele é obtido através da multiplicação entre 2 e 5. Da mesma forma, zero é um inteiro múltiplo de 2 (a saber, ), portanto zero é par.[2]
Também é possível explicar porque zero é par sem se referir a definições formais.[3] As seguintes explicações fazem uso da ideia de que zero é par através de conceitos fundamentais sobre números. A partir destes fundamentos, pode-se prover argumentos racionais para a própria definição — e sua aplicação ao zero.
Explicações básicas[editar | editar código-fonte]

Zero é um número, e números são usados para contagem. Dado um conjunto de objetos, utiliza-se um número para descrever quantos objetos estão no conjunto. Zero representa a conta de nenhum objeto no conjunto; em termos mais formais, é o número de objetos no conjunto vazio. O conceito de paridade é usado para fazer grupos de dois objetos. Se os objetos em um conjunto puderem ser agrupados em duplas, com nenhum objeto sobrando, então o número de objetos é par. Se um objeto é deixado sem par, então o número de objetos no conjunto é ímpar. O conjunto vazio tem zero duplas e nenhum objeto é deixado sem par, portanto zero é par.[5]
Essas ideias podem ser ilustradas ao desenhar-se objetos em duplas. É difícil retratar duplas, ou enfatizar a não existência de um objeto sobrando, então desenhar outros grupos e compará-los com o conjunto com zero duplas ajuda a compreender melhor a ideia. Por exemplo, no grupo de cinco objetos, existem duas duplas e, de modo mais importante, há um objeto sobrando, então 5 é ímpar. No grupo de quatro objetos, por outro lado, não há nenhum objeto sobrando, portanto 4 é par. No grupo de apenas um objeto, não existe nenhuma dupla, e existe um objeto sobrando, portanto 1 é ímpar. No grupo de zero objetos, não há nenhum objeto sobrando, portanto 0 é par.[6]
Existe outra definição concreta da paridade: se os objetos em um conjunto podem ser colocados em dois grupos de mesmo tamanho, então o número de objetos é par. A definição é equivalente a primeira. De novo, zero é par, pois o conjunto vazio pode ser dividido em dois grupos de zero itens cada.[7]
Números também podem ser visualizados como pontos em uma reta numérica. Quando números pares e ímpares são distinguidos uns dos outros, o padrão torna-se óbvio, especialmente se números negativos são incluídos:

Os números pares e ímpares alternam-se. Começando em qualquer número par, contar duas unidades para a esquerda ou para a direita alcança-se outro número par, e não há qualquer razão para ignorar o zero.[8]
Com a introdução da multiplicação, a paridade pode ser abordada de uma maneira mais formal usando expressões aritméticas. Todo inteiro é ou da forma ou da forma ; o primeiro caso representa os números pares e o segundo representa os ímpares. Por exemplo, 1 é ímpar porque , e 0 é par porque . Fazer uma tabela desses fatos reforça o argumento criado pela imagem da reta numérica acima.[9]
| Número inteiro | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Decomposição única | |||||||||
| Paridade | Par | Ímpar | Par | Ímpar | Par | Ímpar | Par | Ímpar | Par |
Definindo paridade[editar | editar código-fonte]
A definição precisa de um termo matemático, tal como "par" significando "inteiro que é múltiplo de dois", é em última análise uma convenção. Diferentemente de "par", alguns termos matemáticos são propositalmente construídos para excluir casos triviais ou degenerados. Números primos são um exemplo famoso. Antes do século XX, definições de primalidade eram inconsistentes, e matemáticos importantes como Goldbach, Lambert, Legendre, Cayley, e Kronecker classificavam 1 como primo.[10] A definição moderna de "número primo" é "inteiro positivo com exatamente 2 divisores", então 1 não é primo. Esta definição pode ser racionalizada ao perceber que ela é mais adequada aos teoremas que dizem respeito aos números primos. Por exemplo, o teorema fundamental da aritmética é mais facilmente enunciável quando 1 não é considerado primo.[11]
Seria possível similarmente redefinir o termo "par" de forma que não mais inclua o zero. Contudo, neste caso, a nova definição tornaria mais difícil enunciar teoremas que dizem respeito aos números pares. O efeito pode ser visto em regras algébricas que regem os números pares e ímpares.[12] As regras mais relevantes dizem respeito a adição, subtração e multiplicação:
- par ± par = par
- ímpar ± ímpar = par
- par × inteiro = par
Inserindo valores apropriados no lado esquerdo dessas regras, pode-se produzir 0 no lado direito:
As regras acima tornar-se-iam incorretas caso zero não fosse par.[12] Na melhor das hipóteses, elas teriam que ser modificadas. Por exemplo, um guia de estudo de teste afirma que números pares são caracterizados como inteiros múltiplos de dois, mas zero não é "nem par nem ímpar".[13] Consequentemente, essas regras contêm exceções:[13]
- par ± par = par (ou zero)
- ímpar ± ímpar = par (ou zero)
- par × inteiro não nulo = par
Fazer uma exceção para zero na definição de paridade força a criação de tais exceções nas regras para números pares. Sob outra perspectiva, tomar as regras obedecidas por números pares positivos e requerer que elas continuem a ser válidas para inteiros força a definição usual e a paridade de zero.[12]
Contextos matemáticos[editar | editar código-fonte]
Incontáveis resultados em teoria dos números são embasadas pelo teorema fundamental da aritmética e pelas propriedades algébricas de números pares, logo as escolhas descritas acima têm amplas consequências. Por exemplo, o fato de números positivos terem fatoração única significa que pode ser determinado se um número tem um número par ou ímpar de fatores primos distintos. Uma vez que 1 não é primo, e também não tem fatores primos, é um produto de 0 primos distintos; como 0 é um número par, 1 tem um número par de fatores primos distintos. Isso implica que a função de Möbius assume o valor , o que é necessário para ela ser uma função multiplicativa e para a fórmula de inversão de Möbius funcionar.[14]
Não sendo ímpar[editar | editar código-fonte]
Um número inteiro é ímpar se existe um número inteiro tal que . Uma maneira de provar que zero não é ímpar é por contradição: se , então , que não é um inteiro.[15] Um resultado clássico da teoria dos grafos diz que um grafo de ordem ímpar (que tem um número ímpar de vértices) sempre tem ao menos um vértice de grau par. (A declaração por si só requer que zero seja par: o grafo nulo tem ordem par e um vértice isolado tem grau par.)[16] Para provar o enunciado, é na verdade mais fácil provar um resultado mais forte: qualquer grafo de ordem ímpar tem um número ímpar de vértices de grau par. A aparição deste número ímpar é explicada por um resultado ainda mais geral, conhecido como o lema do aperto de mão: qualquer grafo tem um número par de vértices de grau ímpar.[17]
O lema de Sperner é uma aplicação mais avançada da mesma estratégia. O lema declara que um certo tipo de coloração em uma triangulação de um simplex tem um subsimplex que contém todas as cores. Em vez de diretamente construir tal subsimplex, é mais conveniente provar que existe um número ímpar de tais subsimplexes através de um argumento indutivo.[18] Uma declaração mais forte do lema então explica porque este número é ímpar: ele naturalmente pode ser separado em quando são consideradas as duas possíveis orientações de um simplex.[19]
Alternação par-ímpar[editar | editar código-fonte]
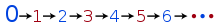
O fato de zero ser par, aliado ao fato de que números pares e ímpares alternam-se, é suficiente para determinar a paridade de todos os outros números naturais. Tal ideia pode ser formalizada em uma definição recursiva do conjunto de números naturais:
- 0 é par;
- é par se e somente se não é par.
Essa definição tem a vantagem conceitual de depender somente dos fundamentos mínimos dos números naturais: a existência de 0 e de sucessores. Como tal, é útil para sistemas de lógica de computador como LF e o provador de teoremas Isabelle.[20] Com essa definição, a paridade de zero não é um teorema, mas um axioma. De fato, "zero é um número par" pode ser interpretado como um dos axiomas de Peano, dos quais os números naturais pares são um modelo.[21] Uma construção similar estende a definição de paridade para números ordinais transfinitos: todo ordinal limite é par, incluindo o zero, e os sucessores de ordinais pares são ímpares.[22]

O teste clássico do ponto em polígono da geometria computacional aplica as ideias acima. Para determinar se um ponto jaz dentro do polígono, cria-se uma semirreta do infinito para o ponto e é contado o número de vezes que ela cruza a borda do polígono. O número de cruzamentos é par se e somente se o ponto estiver fora do polígono. Este algoritmo funciona pois se o raio nunca cruza o polígono, então seu número de cruzamentos é zero, que é par, e o ponto está do lado de fora. Toda vez que a semirreta cruza o polígono, o número de cruzamentos alterna entre par e ímpar, e o ponto na sua extremidade alterna entre estar dentro e estar fora do polígono.[23]

Em teoria dos grafos, um grafo bipartido é um grafo cujos vértices são separados em duas cores, tais que vértices vizinhos tenham cores diferentes. Se um grafo conectado não tem ciclos ímpares, então uma bipartição pode ser construída escolhendo-se um vértice base e colorindo todo vértice em branco ou preto, dependendo se a sua distância de for par ou ímpar. Uma vez que a distância entre e si próprio é 0, e 0 é par, o vértice base é colorido diferentemente dos seus vizinhos, que repousam à distância de 1.[24]
Padrões algébricos[editar | editar código-fonte]

Em álgebra abstrata, os inteiros pares formam várias estruturas algébricas que requerem a inclusão do zero. O fato de que a identidade aditiva (zero) é par, aliado à paridade das somas e dos inverso aditivo de números pares e à associatividade da adição, significa que os inteiros pares formam um grupo. Além disso, o grupo de inteiros pares sob adição é um subgrupo de todos os inteiros; isto é um exemplo elementar do conceito de subgrupo.[16] A observação anterior de que a regra "par — par = par" força 0 a ser par é parte de um padrão geral: qualquer subconjunto não-vazio de um grupo aditivo que é fechado sob subtração precisa ser um subgrupo e, em particular, deve conter a identidade.[25]
Como os inteiros pares formam um subgrupo dos inteiros, eles particionam os inteiros em coclasses. Essas coclasses podem ser descritas como as classes de equivalência da seguinte relação de equivalência: se é par. Aqui, a paridade de zero é diretamente manifestada como a reflexividade da relação binária .[26]
Analogamente, o grupo alternante é um subgrupo de índice 2 no grupo simétrico de n letras. Os elementos do grupo alternante, chamados de permutações pares, são produtos de números pares de transposições. A função identidade, um produto vazio sem transposições, é uma permutação par já que zero é par; ela é o elemento identidade do grupo.[27]
A regra "par × inteiro = par" significa que os números pares formam um ideal no anel dos inteiros, e a relação de equivalência acima pode ser descrita como equivalência módulo tal ideal. Em particular, inteiros pares são exatamente aqueles inteiros que satisfazem . Esta formulação é útil para investigar as raízes inteiras de polinômios.[28]
Ordem 2-aditiva[editar | editar código-fonte]
Há um sentido em que alguns múltiplos de 2 são "mais pares" do que outros. Múltiplos de 4 são chamados duplamente pares, já que eles podem ser divididos por 2 duas vezes. Não somente zero é divisível por 4, como também tem a propriedade única de ser divisível por todas as potências de 2, superando todos os outros números em "paridade".[1]
Uma consequência desse fato aparece na ordenação bit-invertida de tipos de dados inteiros utilizada por alguns algoritmos de computador, como a transformada rápida de Fourier de Cooley-Tukey. Esta ordenação tem a propriedade de que quanto mais para a esquerda o primeiro 1 ocorre na expansão binária de um número, ou quanto mais vezes ele for divisível por 2, mais cedo ele aparecerá. A bit-inversão de zero ainda é zero; ele pode ser dividido por 2 qualquer número de vezes, e sua expansão binária não contém nenhum 1, então ele sempre vem primeiro.[29]
Embora 0 seja divisível por 2 mais vezes do que qualquer outro número, não é tão direto o processo de quantificar exatamente quantas vezes isso ocorre. Para qualquer inteiro n diferente de zero, pode-se definir a ordem 2-aditiva de n como sendo o número de vezes que n é divisível por 2. Esta descrição não funciona para 0; não importa quantas vezes ele seja dividido por 2, sempre pode ser dividido por 2 novamente. Em vez disso, a convenção é configurar a ordem 2-aditiva de 0 como sendo infinita como um caso especial.[30] Esta convenção não é particular à ordem 2-aditiva; é um dos axiomas de uma valoração aditiva em álgebras superiores.[31]
As potências de dois — 1, 2, 4, 8, ... — formam uma sequência simples de números de ordem 2 crescente. Nos números 2-aditivos, tais sequências convergem de fato para zero.[32]
Educação[editar | editar código-fonte]

O assunto da paridade de zero é frequentemente tratado nos primeiros dois ou três anos do ensino primário, à medida que o conceito de números pares e ímpares é introduzido e desenvolvido.[34]
Conhecimento dos estudantes[editar | editar código-fonte]
A tabela à direita[33] retrata as crenças das crianças sobre a paridade do zero à medida que progridem do Ano 1 ao Ano 6 do sistema educacional inglês. Os dados são de Len Frobisher, que realizou um par de levantamentos de crianças em escolas na Inglaterra. Frobisher estava interessado em saber como o conhecimento da paridade de um único dígito se traduz no conhecimento da paridade de múltiplos dígitos, e o zero aparece proeminente nos resultados.[35]
Em uma pesquisa preliminar com cerca de 400 crianças de sete anos, 45% delas escolheram par ao invés de ímpar quando perguntadas sobre a paridade do zero.[36] Uma pesquisa posterior ofereceu mais escolhas: nenhum dos dois, ambos e não sei. Desta vez, o número de crianças na mesma faixa etária que identificou zero como par caiu para 32%.[37] O acerto na decisão de que o zero é par inicialmente aumenta e então se estabiliza por volta de 50% nos Anos 3 a 6.[38] Em comparação, a tarefa mais fácil, identificar a paridade de um único dígito, atinge cerca de 85% de sucesso.[39]
Em entrevistas, Frobisher suscitou o raciocínio dos alunos. Um aluno de quinto ano decidiu que 0 era par porque foi encontrado na tabela de multiplicação do 2. Uma dupla de alunos de quarto ano percebeu que zero pode ser dividido em duas partes iguais. Outro quartanista raciocinou que como "1 é ímpar, se eu descer é par".[40] As entrevistas também revelaram os equívocos por trás de respostas incorretas. Um aluno de segundo ano estava "bastante convencido" de que zero era ímpar, comentando "é o primeiro número que você conta" em sua resposta.[41] Um quartanista referiu-se a 0 como "nenhum" e pensou que não era nem ímpar nem par, já que "não era um número".[42] Em outro estudo, Annie Keith observou uma classe de 15 estudantes do segundo ano[a] que se convenceram de que zero era um número par com base na alternância ímpar-par e na possibilidade de dividir um grupo de zero coisas em dois grupos de igual tamanho.[43]
Pesquisas mais aprofundadas foram realizadas por Esther Levenson, Pessia Tsamir e Dina Tirosh, que entrevistaram um par de estudantes de sexto ano que estavam tendo alto desempenho em sua aula de matemática. Um estudante preferiu as explicações dedutivas das alegações matemáticas, enquanto o outro preferiu exemplos práticos. Ambos os alunos inicialmente pensaram que 0 não era nem ímpar, nem par, por diferentes motivos. Levenson et al. demonstrou como o raciocínio dos alunos refletiu seus conceitos de zero e divisão.[44]
| Afirmações feitas por estudantes[45] |
|---|
| "Zero não é nem par nem ímpar." |
| "Zero poderia ser par." |
| "Zero não é ímpar." |
| "Zero tem que ser par." |
| "Zero não é um número par." |
| "Zero sempre será um número par." |
| "Zero nem sempre será um número par." |
| "Zero é par." |
| "Zero é especial." |
Deborah Loewenberg Ball analisou as ideias de alunos da terceira série sobre números pares e ímpares e o zero, que eles tinham acabado de discutir com um grupo de alunos do quarto ano. Os alunos discutiram a paridade de zero, as regras para os números pares, e como a matemática é feita. As afirmações sobre zero assumiram muitas formas, como mostrado na lista à direita.[45] Ball e seus coautores argumentaram que o episódio demonstrou como os alunos podem "fazer matemática na escola", ao contrário da redução usual da disciplina à solução mecânica de exercícios.[46]
Um dos temas da literatura de pesquisa é a tensão entre as imagens conceituais dos alunos sobre a paridade e suas definições conceituais.[47] Ambos os alunos do sexto ano de Levenson et al. definiram números pares como múltiplos de 2 ou números divisíveis por 2, mas inicialmente não conseguiram aplicar essa definição a zero, porque não tinham certeza de como multiplicar ou dividir zero por 2. O entrevistador eventualmente os levou a concluir que zero era par; os alunos tomaram diferentes rotas para essa conclusão, com base em uma combinação de imagens, definições, explicações práticas, e explicações abstratas. Em outro estudo, David Dickerson e Damien Pitman examinaram o uso de definições por cinco estudantes de graduação em matemática. Eles descobriram que os alunos de graduação conseguiram em grande parte aplicar a definição de "par" a zero, mas ainda não estavam convencidos por esse raciocínio, uma vez que entrava em conflito com suas imagens conceituais.[48]
Conhecimento dos professores[editar | editar código-fonte]
Pesquisadores de educação matemática na Universidade de Michigan tem incluído o prompt verdadeiro-ou-falso "0 é um número par" em um banco de dados de mais de 250 perguntas projetadas para medir o conhecimento do conteúdo de professores. Para eles, a questão exemplifica "conhecimento comum ... que qualquer adulto bem educado deveria ter", e é "ideologicamente neutro" na medida em que a resposta não varia entre a matemática tradicional e a matemática reformada. Em um estudo de 2000 a 2004 com 700 professores de ensino primário nos Estados Unidos, o desempenho geral nessas questões previu melhorias significativas nos resultados dos exames padronizados dos alunos após terem feito as aulas com esses professores.[49] Em um estudo mais aprofundado de 2008, os pesquisadores encontraram uma escola onde todos os professores achavam que zero não era nem ímpar, nem par, incluindo um professor que era considerado exemplar em todas as medidas. O equívoco foi espalhado por um instrutor de matemática em seu prédio.[50]
É incerto quantos professores mantém equívocos sobre o zero. Os estudos de Michigan não publicaram os dados por questões individuais. Betty Lichtenberg, professora associada de educação matemática na Universidade do Sul da Flórida, em um estudo de 1972 informou que, quando um grupo de futuros professores da escola primária receberam um teste verdadeiro-ou-falso incluindo o item "Zero é um número par", eles achavam que era uma "pegadinha", com cerca de dois terços respondendo "Falso".[51]
Implicações para instrução[editar | editar código-fonte]
Matematicamente, provar que zero é par é uma questão simples de aplicar uma definição, mas é necessária mais explicação no contexto da educação. Um problema diz respeito aos fundamentos da prova; A definição de "par" como "múltiplo inteiro de 2" nem sempre é apropriada. Um aluno nos primeiros anos de ensino primário pode ainda não ter aprendido o que "inteiro" ou "múltiplo" significa, e muito menos como se multiplicar com 0.[52] Além disso, indicar uma definição de paridade para todos os números inteiros pode parecer um atalho conceitual arbitrário se os únicos números pares investigados até então tiverem sido os positivos. Isso pode ajudar a reconhecer que, à medida que o conceito de número é estendido de inteiros positivos para incluir o zero e inteiros negativos, propriedades de número como a paridade também são estendidas de forma não trivial.[53]
Cognição numérica[editar | editar código-fonte]

Os adultos que acreditam que o zero é par podem, no entanto, não estar familiarizados em rotulá-lo como par, o suficiente para retardá-los significativamente em um experimento de tempo de reação. Stanislas Dehaene, pioneira no campo da cognição numérica, liderou uma série desses experimentos no início da década de 1990. Um numeral ou o nome de um número é exibido para o sujeito em um monitor, e um computador registra o tempo que o sujeito leva para pressionar um dos dois botões para identificar o número como par ou ímpar. Os resultados mostraram que 0 foi mais lento para ser processado pelos sujeitos do que outros números pares. Algumas variações do experimento encontraram atrasos de até 60 milissegundos, ou cerca de 10% do tempo médio de reação — uma pequena, mas significativa diferença.[55]
Os experimentos de Dehaene não foram projetados especificamente para investigar o zero, mas para comparar modelos concorrentes de como a informação de paridade é processada e extraída. O modelo mais específico, a hipótese de cálculo mental, sugere que as reações a 0 devem ser rápidas; 0 é um número pequeno, e é fácil calcular (Os indivíduos calculam e nomeiam o resultado da multiplicação por zero mais rápido do que a multiplicação por números não-nulos, embora sejam mais lentos para verificar resultados propostos como ). Os resultados dos experimentos sugeriram que algo bastante diferente estava acontecendo: a informação de paridade foi aparentemente recuperada da memória, juntamente com um conjunto de propriedades relacionadas, tais como ser número primo ou uma potência de dois. Tanto a sequência de potências de dois quanto a sequência de números pares positivos 2, 4, 6, 8, ... são categorias mentais bem distinguidas cujos membros são prototipicamente pares. Zero não pertence a nenhuma lista, daí as respostas mais lentas.[56]
Repetidos experimentos mostraram um atraso em relação ao zero para sujeitos com várias idades e origens nacionais e linguísticas, confrontados com nomes de números em forma de numeral, soletrados e soletrados em uma imagem espelhada. O grupo de Dehaene encontrou um fator diferenciador: conhecimentos matemáticos. Em uma de suas experiências, os alunos da Escola Normal Superior de Paris foram divididos em dois grupos: aqueles de estudos literários e aqueles que estudam matemática, física ou biologia. O desaceleramento em 0 foi "essencialmente encontrado no grupo [literário]" e, de fato, "antes do experimento, alguns sujeitos [literários] não tinham certeza se era par ou ímpar e tinham que lembrar a definição matemática".[57]
Esta forte dependência da familiaridade enfraquece de novo a hipótese de cálculo mental.[58] O efeito também sugere que não é apropriado incluir zero em experimentos onde os números pares e ímpares são comparados como um grupo. Como diz um estudo, "a maioria dos pesquisadores parece concordar que zero não é um número par típico e não deve ser investigado como parte da linha mental dos números".[59]
Contextos cotidianos[editar | editar código-fonte]
Alguns dos contextos onde a paridade de zero aparece são puramente retóricos. A questão fornece material para fóruns na Internet e sites de perguntas.[60] O linguista Joseph Grimes acredita que perguntar "zero é um número par?" para casais é uma boa maneira de fazê-los discordar.[61] As pessoas que pensam que zero não é nem par nem ímpar podem usar a paridade de zero como prova de que cada regra tem um contraexemplo,[62] ou como um exemplo de uma "pegadinha".[63]
Por volta do ano 2000, os meios de comunicação notaram um par de marcos incomuns: "19/11/1999" foi a última data de calendário composta por todos os dígitos ímpares que vai ocorrer por muito tempo (a próxima data composta somente por números ímpares será 11/11/3111), e "02/02/2000" foi a primeira data toda par a ocorrer em muito tempo (a data composta somente por dígitos pares anterior foi 28/08/888, se o calendário gregoriano puder ser usado retroativamente a sua promulgação).[64] Como esses resultados fazem uso de 0 sendo par, alguns leitores discordaram da ideia.[65]
Em testes padronizados, se uma questão pergunta sobre o comportamento de números pares, pode ser necessário ter em mente que zero é par.[66] As publicações oficiais relativas aos testes GMAT e GRE estabelecem que 0 é par.[67]
A paridade de zero é relevante para o rodízio ímpar-par, em que os motoristas de carros podem dirigir ou comprar gasolina em dias alternados, de acordo com a paridade do último dígito em suas placas. A metade dos números em uma determinada gama termina em 0, 2, 4, 6, 8 e a outra metade em 1, 3, 5, 7, 9, então faz sentido incluir 0 com os outros números pares. No entanto, em 1977, um sistema de racionamento de Paris levou à confusão: em um dia ímpar, a polícia evitou multar motoristas cujas placas terminavam em 0, porque não sabiam se 0 era par ou não. Para evitar tal confusão, a legislação pertinente às vezes estipula que zero é par;[68] Tais leis foram aprovadas em Nova Gales do Sul[69] e Maryland.[70] Em São Paulo, o rodízio é feito de forma distinta e não parece levar em conta essa questão sobre a paridade do zero: na segunda-feira ficam proibidos de circular em determinada área carros de placas 1 e 2, na terça-feira, os carros de finais de placa 3 e 4 não circulam, na quarta-feira os de final 5 e 6, na quinta-feira os de final 7 e 8 e finalmente na sexta-feira, os de final 9 e 0.[71]
Nos navios da Marinha dos Estados Unidos, os compartimentos de números pares ficam ao lado da porta, mas o número zero é reservado para compartimentos que cruzam a linha central do navio. Ou seja, os números são lidos 6-4-2-0-1-3-5 da porta a estibordo.[72] No jogo da roleta, o número 0 não conta como par ou ímpar, dando ao cassino uma vantagem em tais apostas.[73] Da mesma forma, a paridade de zero pode afetar as recompensas em apostas quando o resultado depende de algum número aleatório ser ímpar ou par, e resulta ser zero.[74]
O jogo de "par ou ímpar" também é afetado: se ambos os jogadores lançam zero dedos, o número total de dedos é zero, então o jogador par ganha.[75] Um manual para professores sugere jogar este jogo como uma forma de introduzir as crianças no conceito de que 0 é divisível por 2.[76]
Notas
- ↑ No sentido estadunidense ou canadense do termo.
Referências
- ↑ a b Arnold 1919, p. 21 "Pelo mesmo teste zero supera todos os números em 'paridade'."; Wong 1997, p. 479 "Portanto, o inteiro b000⋯000 = 0 é o mais 'par'."
- ↑ Penner 1999, p. 34: Lema B.2.2, O inteiro 0 é par e não é ímpar. Penner usa o símbolo matemático ∃, a quantificação existencial, para estabelecer a prova: "Para ver que 0 é par, nós devemos provar que ∃k (0 = 2k), e isto segue da igualdade 0 = 2 ⋅ 0."
- ↑ Ball, Lewis & Thames 2008, p. 15 discute este desafio para professores das séries primárias, que querem dar razoes matemáticas para fatos matemáticos, mas cujos estudantes nem usam a mesma definição, nem poderiam entendê-la se fosse introduzida.
- ↑ Compare Lichtenberg 1972, p. 535 Fig. 1
- ↑ Lichtenberg 1972, pp. 535–536 " ... números respondem a questão 'Quantos?' para o conjunto de objetos ... zero é o número propriedade do conjunto vazio ... Se os elementos de cada conjunto são marados em grupos de dois ... então o número desse conjunto é um número par."
- ↑ Lichtenberg 1972, pp. 535–536 "Zero grupos de estrelas são circuladas. Nenhuma estrela sobra. Assim sendo, zero é um número par."
- ↑ Dickerson & Pitman 2012, p. 191.
- ↑ Lichtenberg 1972, p. 537; compare sua Fig. 3. "Se os números pares são identificados em alguma maneira especial ... não existe razão alguma para omitir zero do padrão."
- ↑ Lichtenberg 1972, pp. 537–538 "Em um nível mais avançado ... números expressos como (2 × ▢) + 0 são números pares ... zero se encaixa muito bem nesse padrão."
- ↑ Caldwell & Xiong 2012, pp. 5–6.
- ↑ Gowers 2002, p. 118 "A exclusão aparentemente arbitrária de 1 da definição de primo ... não expressa um fato profundo sobre os números: simplesmente é uma convenção útil, adotada, de modo que existe apenas uma maneira de fatorizar qualquer número dado em números primos." Para um mais discussão mais detalhada, veja Caldwell & Xiong 2012.
- ↑ a b c Partee 1978, p. xxi
- ↑ a b Stewart 2001, p. 54 Estas regras são dadas, mas elas não são citadas textualmente.
- ↑ Devlin 1985, pp. 30–33
- ↑ Penner 1999, p. 34.
- ↑ a b Berlinghoff, Grant & Skrien 2001 Para vértices isolados veja p. 149; para grupos veja p.311.
- ↑ Lovász, Pelikán & Vesztergombi 2003, pp. 127–128
- ↑ Starr 1997, pp. 58–62
- ↑ Border 1985, pp. 23–25
- ↑ Lorentz 1994, pp. 5–6; Lovas & Pfenning 2008, p. 115; Nipkow, Paulson & Wenzel 2002, p. 127
- ↑ Bunch 1982, p. 165
- ↑ Salzmann et al. 2007, p. 168
- ↑ Wise 2002, pp. 66–67
- ↑ Anderson 2001, p. 53; Hartsfield & Ringel 2003, p. 28
- ↑ Dummit & Foote 1999, p. 48
- ↑ Andrews 1990, p. 100
- ↑ Tabachnikova & Smith 2000, p. 99; Anderson & Feil 2005, pp. 437–438
- ↑ Barbeau 2003, p. 98
- ↑ Wong 1997, p. 479
- ↑ Gouvêa 1997, p. 25 De um primo p geral: "A razão aqui é que nós podemos certamente dividir 0 por p, e a resposta é 0, que podemos dividir por p ..." (elipses no original)
- ↑ Krantz 2001, p. 4
- ↑ Salzmann et al. 2007, p. 224
- ↑ a b Frobisher 1999, p. 41
- ↑ Este é o prazo nos Estados Unidos, Canadá, Grã Bretanha, Austrália e Israel; veja Levenson, Tsamir & Tirosh 2007, p. 85.
- ↑ Frobisher 1999, pp. 31 (Introdução); 40–41 (O número zero); 48 (Implicações para o ensino)
- ↑ Frobisher 1999, pp. 37, 40, 42; os resultados são da pesquisa realizada no meio das férias de verão de 1992.
- ↑ Frobisher 1999, p. 41 "A porcentagem de crianças do segundo ano decidindo que zero é um número par é muito menor que no estudo anterior, 32 porcento contra 45 porcento"
- ↑ Frobisher 1999, p. 41 "O sucesso em decidir que zero é um número par não continua a crescer com a idade, com aproximadamente uma em duas crianças dos anos 2 a 6 colocando um tiquetaque na caixa dos 'pares' ..."
- ↑ Frobisher 1999, pp. 40–42, 47; estes resultados são do estudo de fevereiro de 1999, incluindo 481 crianças, de três escolas em uma variedade de níveis de conhecimento.
- ↑ Frobisher 1999, p. 41, atribuído a "Jonathan"
- ↑ Frobisher 1999, p. 41, atribuído a "Joseph"
- ↑ Frobisher 1999, p. 41, atribuido a "Richard"
- ↑ Keith 2006, pp. 35–68 "Havia pouco desentendimento com a ideia de que zero era um número par. Os estudantes convenceram os poucos que não tinham certeza com dois argumentos: O primeiro argumento era que os números entram em um padrão ... ímpar, par, ímpar, par, ímpar, par ... e uma vez que dois é par e um é ímpar, então o número antes de um, que não é uma fração, seria zero. Então, zero precisaria ser par; O segundo argumento foi que, se uma pessoa tem zero coisas e as colocou em dois grupos iguais, haveria zero em cada grupo. Os dois grupos teriam a mesma quantidade: zero."
- ↑ Levenson, Tsamir & Tirosh 2007, pp. 83–95
- ↑ a b Ball, Lewis & Thames 2008, p. 27, Figure 1.5 "Mathematical claims about zero."
- ↑ Ball, Lewis & Thames 2008, p. 16.
- ↑ Levenson, Tsamir & Tirosh 2007; Dickerson & Pitman 2012
- ↑ Dickerson & Pitman 2012.
- ↑ Ball, Hill & Bass 2005, pp. 14–16
- ↑ Hill et al. 2008, pp. 446–447.
- ↑ Lichtenberg 1972, p. 535
- ↑ Ball, Lewis & Thames 2008, p. 15. Veja também as notas de Ball para discussão futura de definições apropriadas.
- ↑ Como concluído por Levenson, Tsamir & Tirosh 2007, p. 93, referenciando Freudenthal 1983, p. 460
- ↑ Nuerk, Iversen & Willmes 2004, p. 851: "Também pode ser visto que zero difere fortemente de todos os outros números, independentemente de ser respondido com a mão esquerda ou direita. (Veja a linha que separa zero dos outros números)"
- ↑ Veja os dados em Dehaene, Bossini & Giraux 1993, e resumido por Nuerk, Iversen & Willmes 2004, p. 837.
- ↑ Dehaene, Bossini & Giraux 1993, pp. 374–376
- ↑ Dehaene, Bossini & Giraux 1993, pp. 376–377
- ↑ Dehaene, Bossini & Giraux 1993, p. 376 "Em algum sentido intuitivo, a noção de paridade é familiar apenas para números maiores do que 2. Na verdade, antes do experimento, alguns sujeitos L não tinham certeza se 0 era ímpar ou par e precisava ser lembrado da definição matemática. A evidência, em resumo, sugere que, em vez de ser calculado on-line, usando um critério de divisibilidade por 2, a informação de paridade é recuperada da memória juntamente com várias outras propriedades semânticas ... Se uma memória semântica for acessada em julgamentos de paridade, então as diferenças interindividuais devem ser encontradas dependendo da familiaridade dos sujeitos com conceitos de números".
- ↑ Nuerk, Iversen & Willmes 2004, pp. 838, 860–861
- ↑ The Math Forum participants 2000; Straight Dope Science Advisory Board 1999; Doctor Rick 2001
- ↑ Grimes 1975, p. 156 "...pode-se colocar as seguintes questões para casais do seu conhecimento: (1) é zero um número par? ... Muitos casais discordam..."
- ↑ Wilden & Hammer 1987, p. 104
- ↑ Snow 2001; Morgan 2001
- ↑ Steinberg 1999; Siegel 1999; Stingl 2006
- ↑ Sones & Sones 2002 "Segue que zero é par, e que 20/02/2000 quebra o quebra-cabeça. No entanto, sempre é surpreendente o quanto as pessoas estão incomodadas ao chamar zero de par... "; Column 8 readers 2006a" '... de acordo com matemáticos, o número zero, juntamente com números negativos e frações, é nem par nem ímpar", escreve Etan ..."; Column 8 readers 2006b "'Eu concordo que zero é par, mas o Professor Bunder é sábio para "provar" afirmando que 0 = 2 x 0? Por essa lógica (de um PhD em lógica matemática, não menos), como 0 = 1 x 0, também é ímpar! O professor disputará isso e, logicamente, ele tem uma base sólida para fazê-lo, mas podemos estar usando este tópico um pouco fino ... "
- ↑ Kaplan Staff 2004, p. 227
- ↑ Graduate Management Admission Council 2005, pp. 108, 295–297; Educational Testing Service 2009, p. 1
- ↑ Arsham 2002; As aspassão atribuídas ao heute broadcast de 1º de outubro de 1977. A conta de Arsham é repetida por Crumpacker 2007, p. 165.
- ↑ Sones & Sones 2002 "O matemático de Penn State, George Andrews, que lembra um tempo de racionamento de gás na Austrália ... Então alguém no parlamento de Nova Gales do Sul afirmou que isso significava que as placas que terminavam em zero nunca poderiam obter gás, porque 'zero não é ímpar ou par". Assim, o parlamento de Nova Gales do Sul decidiu que, para fins de racionamento de gás, zero é um número par!'"
- ↑ Uma lei de 1980 de Maryland especifica: "(a) Em datas de calendário numeradas pares gasolina deverá somente ser comprada por operadores de veículos tendo placas de registro personalizadas contendo nenhum número e placas de registro com o último dígito terminando em um número par. Isto não deve incluir placas de rádio amador. Zero é um número par; (b) Em datas numeradas ímpares ..." aspas parciais tomadas de Laws of the State of Maryland, Volume 2 - 1974 do Department of Legislative Reference, disponível aqui, p. 3236}}
- ↑ «Decreto nº 37.085 - de 3 de outubro de 1997» (PDF). Prefeitura de São Paulo apud site da CET. 3 de outubro de 1997. Consultado em 11 de julho de 2017
- ↑ Cutler 2008, pp. 237–238
- ↑ Brisman 2004, p. 153
- ↑ Smock 2006; Hohmann 2007; Turner 1996
- ↑ Diagram Group 1983, p. 213
- ↑ Baroody & Coslick 1998, p. 1.33
Bibliografia[editar | editar código-fonte]
- Anderson, Ian (2001). A First Course in Discrete Mathematics. London: Springer. ISBN 1-85233-236-0
- Anderson, Marlow; Feil, Todd (2005). A First Course in Abstract Algebra: Rings, Groups, And Fields. London: CRC Press. ISBN 1-58488-515-7
- Andrews, Edna (1990). Markedness Theory: the union of asymmetry and semiosis in language. Durham: Duke University Press. ISBN 0-8223-0959-9
- Arnold, C. L. (1919). The Number Zero. The Ohio Educational Monthly. 68. [S.l.: s.n.] pp. 21–22. Consultado em 11 de abril de 2010
- Arsham, Hossein (2002). Zero in Four Dimensions: Historical, Psychological, Cultural, and Logical Perspectives. The Pantaneto Forum. [S.l.: s.n.] Consultado em 24 de setembro de 2007. Cópia arquivada em 11 de março de 2017
- Ball, Deborah Loewenberg; Hill, Heather C.; Bass, Hyman (2005). Knowing Mathematics for Teaching: Who Knows Mathematics Well Enough To Teach Third Grade, and How Can We Decide? (PDF). American Educator. [S.l.: s.n.] Consultado em 16 de setembro de 2007
- Ball, Deborah Loewenberg; Lewis, Jennifer; Thames, Mark Hoover (2008). Making mathematics work in school (PDF). Journal for Research in Mathematics Education. M14. [S.l.: s.n.] pp. 13–44 and 195–200. Consultado em 4 de março de 2010. Cópia arquivada (PDF) em 20 de dezembro de 2010
- Barbeau, Edward Joseph (2003). Polynomials. [S.l.]: Springer. ISBN 0-387-40627-1
- Baroody, Arthur; Coslick, Ronald (1998). Fostering Children's Mathematical Power: An Investigative Approach to K-8. [S.l.]: Lawrence Erlbaum Associates. ISBN 0-8058-3105-3
- Berlinghoff, William P.; Grant, Kerry E.; Skrien, Dale (2001). A Mathematics Sampler: Topics for the Liberal Arts 5th rev. ed. [S.l.]: Rowman & Littlefield. ISBN 0-7425-0202-3
- Border, Kim C. (1985). Fixed Point Theorems with Applications to Economics and Game Theory. [S.l.]: Cambridge University Press. ISBN 0-521-38808-2
- Brisman, Andrew (2004). Mensa Guide to Casino Gambling: Winning Ways. [S.l.]: Sterling. ISBN 1-4027-1300-2
- Bunch, Bryan H. (1982). Mathematical Fallacies and Paradoxes. [S.l.]: Van Nostrand Reinhold. ISBN 0-442-24905-5
- Caldwell, Chris K.; Xiong, Yeng (27 de dezembro de 2012). What is the Smallest Prime?. Journal of Integer Sequences. 15. [S.l.: s.n.] arXiv:1209.2007

- Column 8 readers (10 de março de 2006). Column 8. The Sydney Morning Herald First ed. [S.l.: s.n.] p. 18
- Column 8 readers (16 de março de 2006). Column 8. The Sydney Morning Herald First ed. [S.l.: s.n.] p. 20
- Crumpacker, Bunny (2007). Perfect Figures: The Lore of Numbers and How We Learned to Count. [S.l.]: Macmillan. ISBN 0-312-36005-3
- Cutler, Thomas J. (2008). The Bluejacket's Manual: United States Navy Centennial ed. [S.l.]: Naval Institute Press. ISBN 1-55750-221-8
- Dehaene, Stanislas; Bossini, Serge; Giraux, Pascal (1993). The mental representation of parity and numerical magnitude (PDF). Journal of Experimental Psychology: General. 122. [S.l.: s.n.] pp. 371–396. doi:10.1037/0096-3445.122.3.371. Consultado em 13 de setembro de 2007
- Devlin, Keith (1985). The golden age of mathematics. New Scientist. 106. [S.l.: s.n.]
- Diagram Group (1983). The Official World Encyclopedia of Sports and Games. [S.l.]: Paddington Press. ISBN 0-448-22202-7
- Dickerson, David S; Pitman, Damien J (2012). Tai-Yih Tso, ed. Advanced college-level students' categorization and use of mathematical definitions (PDF). Proceedings of the 36th Conference of the International Group for the Psychology of Mathematics Education. 2. [S.l.: s.n.] pp. 187–195
- Dummit, David S.; Foote, Richard M. (1999). Abstract Algebra 2e ed. New York: Wiley. ISBN 0-471-36857-1
- Educational Testing Service (2009). Mathematical Conventions for the Quantitative Reasoning Measure of the GRE® revised General Test (PDF). [S.l.]: Educational Testing Service. Consultado em 6 de setembro de 2011
- Freudenthal, H. (1983). Didactical phenomenology of mathematical structures. Dordrecht, The Netherlands: Reidel
- Frobisher, Len (1999). Anthony Orton, ed. Primary School Children's Knowledge of Odd and Even Numbers. London: Cassell. pp. 31–48
- Gouvêa, Fernando Quadros (1997). p-adic numbers: an introduction 2nd ed. [S.l.]: Springer-Verlag. ISBN 3-540-62911-4
- Gowers, Timothy (2002). Mathematics: A Very Short Introduction. [S.l.]: Oxford University Press. ISBN 978-0-19-285361-5
- Graduate Management Admission Council (2005). The Official Guide for GMAT Review 11th ed. McLean, VA: Graduate Management Admission Council. ISBN 0-9765709-0-4
- Grimes, Joseph E. (1975). The Thread of Discourse. [S.l.]: Walter de Gruyter. ISBN 90-279-3164-X
- Hartsfield, Nora; Ringel, Gerhard (2003). Pearls in Graph Theory: A Comprehensive Introduction. Mineola: Courier Dover. ISBN 0-486-43232-7
- Hill, Heather C.; Blunk, Merrie L.; Charalambous, Charalambos Y.; Lewis, Jennifer M.; Phelps, Geoffrey C.; Sleep, Laurie; Ball, Deborah Loewenberg (2008). Mathematical Knowledge for Teaching and the Mathematical Quality of Instruction: An Exploratory Study. Cognition and Instruction. 26. [S.l.: s.n.] pp. 430–511. doi:10.1080/07370000802177235
- Hohmann, George (25 de outubro de 2007). Companies let market determine new name. [S.l.: s.n.] p. P1C
- Kaplan Staff (2004). Kaplan SAT 2400, 2005 Edition. [S.l.]: Simon and Schuster. ISBN 0-7432-6035-X
- Keith, Annie (2006). Mathematical Argument in a Second Grade Class: Generating and Justifying Generalized Statements about Odd and Even Numbers. [S.l.]: IAP. ISBN 1-59311-495-8
- Krantz, Steven George (2001). Dictionary of algebra, arithmetic, and trigonometry. [S.l.]: CRC Press. ISBN 1-58488-052-X
- Levenson, Esther; Tsamir, Pessia; Tirosh, Dina (2007). Neither even nor odd: Sixth grade students' dilemmas regarding the parity of zero. The Journal of Mathematical Behavior. 26. [S.l.: s.n.] pp. 83–95. doi:10.1016/j.jmathb.2007.05.004
- Lichtenberg, Betty Plunkett (1972). Zero is an even number. The Arithmetic Teacher. 19. [S.l.: s.n.] pp. 535–538
- Lorentz, Richard J. (1994). Recursive Algorithms. [S.l.]: Intellect Books. ISBN 1-56750-037-4
- Lovas, William; Pfenning, Frank (22 de janeiro de 2008). A Bidirectional Refinement Type System for LF. Electronic Notes in Theoretical Computer Science. 196. [S.l.: s.n.] pp. 113–128. doi:10.1016/j.entcs.2007.09.021. Consultado em 16 de junho de 2012
- Lovász, László; Pelikán, József; Vesztergombi, Katalin L. (2003). Discrete Mathematics: Elementary and Beyond. [S.l.]: Springer. ISBN 0-387-95585-2
- Morgan, Frank (5 de abril de 2001). Old Coins. Frank Morgan's Math Chat. [S.l.]: The Mathematical Association of America. Consultado em 22 de agosto de 2009. Cópia arquivada em 8 de janeiro de 2009
- Nipkow, Tobias; Paulson, Lawrence C.; Wenzel, Markus (2002). Isabelle/Hol: A Proof Assistant for Higher-Order Logic. [S.l.]: Springer. ISBN 3-540-43376-7
- Nuerk, Hans-Christoph; Iversen, Wiebke; Willmes, Klaus (2004). Notational modulation of the SNARC and the MARC (linguistic markedness of response codes) effect. The Quarterly Journal of Experimental Psychology A. 57. [S.l.: s.n.] pp. 835–863. doi:10.1080/02724980343000512
- Partee, Barbara Hall (1978). Fundamentals of Mathematics for Linguistics. Dordrecht: D. Reidel. ISBN 90-277-0809-6
- Penner, Robert C. (1999). Discrete Mathematics: Proof Techniques and Mathematical Structures. River Edje: World Scientific. ISBN 981-02-4088-0
- Salzmann, H.; Grundhöfer, T.; Hähl, H.; Löwen, R. (2007). The Classical Fields: Structural Features of the Real and Rational Numbers. [S.l.]: Cambridge University Press. ISBN 0-521-86516-6
- Siegel, Robert (19 de novembro de 1999). Analysis: Today's date is signified in abbreviations using only odd numbers. 1-1, 1-9, 1-9-9-9. The next time that happens will be more than a thousand years from now. All Things Considered. [S.l.]: National Public Radio
- Smock, Doug (6 de fevereiro de 2006). The odd bets: Hines Ward vs. Tiger Woods. Charleston Gazette. [S.l.: s.n.] p. P1B
- Snow, Tony (23 de fevereiro de 2001). Bubba's fools. Jewish World Review. [S.l.: s.n.] Consultado em 22 de agosto de 2009
- Sones, Bill; Sones, Rich (8 de maio de 2002). To hide your age, button your lips. Deseret News. [S.l.: s.n.] p. C07. Consultado em 21 de junho de 2014
- Starr, Ross M. (1997). General Equilibrium Theory: An Introduction. [S.l.]: Cambridge University Press. ISBN 0-521-56473-5
- Steinberg, Neil (30 de novembro de 1999). Even year, odd facts. Chicago Sun-Times 5XS ed. [S.l.: s.n.] p. 50
- Stewart, Mark Alan (2001). 30 Days to the GMAT CAT. Stamford: Thomson. ISBN 0-7689-0635-0
- Stingl, Jim (5 de abril de 2006). 01:02:03 04/05/06; We can count on some things in life. Milwaukee Journal Sentinel Final ed. [S.l.: s.n.] p. B1. Consultado em 21 de junho de 2014. Cópia arquivada em 27 de abril de 2006
- Tabachnikova, Olga M.; Smith, Geoff C. (2000). Topics in Group Theory. London: Springer. ISBN 1-85233-235-2
- The Math Forum participants (2000). A question around zero. Math Forum » Discussions » History » Historia-Matematica. [S.l.]: Drexel University. Consultado em 25 de setembro de 2007
- Turner, Julian (13 de julho de 1996). Sports Betting – For Lytham Look to the South Pacific. The Guardian. [S.l.: s.n.] p. 23
- Wilden, Anthony; Hammer, Rhonda (1987). The rules are no game: the strategy of communication. [S.l.]: Routledge Kegan & Paul. ISBN 0-7100-9868-5
- Wise, Stephen (2002). GIS Basics. [S.l.]: CRC Press. ISBN 0-415-24651-2
- Wong, Samuel Shaw Ming (1997). Computational Methods in Physics and Engineering. [S.l.]: World Scientific. ISBN 981-02-3043-5
Ligações externas[editar | editar código-fonte]
 Media relacionados com Paridade do zero no Wikimedia Commons
Media relacionados com Paridade do zero no Wikimedia Commons


 French
French Deutsch
Deutsch









































