Substitution explicite — Wikipédia
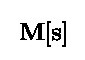
Un calcul de substitutions explicites est une extension du lambda-calcul dans lequel la substitution est intégrée au calcul au même titre que le sont l'abstraction ou l'application, alors que dans le lambda-calcul, la substitution fait partie de la métathéorie, c'est-à-dire qu'elle est définie en dehors de la théorie du lambda-calcul.
Principe[modifier | modifier le code]
L'idée qui conduit à expliciter les substitutions vient du souhait de traiter la substitution comme une opération à part entière du calcul en l'intégrant dans la syntaxe et en y adjoignant un certain nombre de règles qui distribuent et appliquent la substitution et qui font partie du calcul au même titre que la β-réduction fait partie du lambda-calcul. L'intérêt d'intégrer la substitution dans le calcul est de pouvoir parler de la substitution aussi bien en termes d'implantation, de complexité, d'efficacité ou de stratégie d'évaluation que dans ses rapports avec la β-réduction. On peut ainsi expliquer le partage, l'évaluation retardée ou paresseuse ou l'évaluation immédiate. Une substitution qui apparaît dans un terme peut-être évaluée immédiatement ou son évaluation peut être remise à plus tard, à un moment où on aura besoin d'elle. De plus, l'évaluation d'une substitution peut servir à plusieurs endroits et ne nécessiter qu'un seul calcul (partage).
Syntaxe enrichie[modifier | modifier le code]
Pour que le système formel puisse parler à la fois d'abstraction et d'application aussi bien que de substitution, il faut enrichir la syntaxe du lambda-calcul avec un opérateur de substitution explicite. Il y a deux façons de le faire, suivant que l'on travaille avec des variables explicites ou avec des indices de de Bruijn.
- Si les variables sont explicites, on ajoute un opérateur 〈x:=N〉. Dans ce cas, la notation P〈x:=N〉 dénote l'opérateur de substitution explicite appliqué à P et signifie que l'on veut remplacer x par N dans P. On notera que dans l'expression P〈x:=N〉, 〈x:=N〉 est un lieur pour x dans P au même titre que λ est un lieur pour x dans λx.P. Cela a bien sûr une répercussion sur la notion de variable libre qui doit être libre pour λ mais aussi pour 〈x:=N〉.
- Si des indices de Bruijn sont utilisés pour coder les variables, on ajoute un opérateur [s] où s est une substitution. La notation M[s] signifie que M est modifié par la substitution s. Dans ce cas, les substitutions forment une autre sorte d'objets. Elles sont engendrées par des opérateurs spécifiques /, ⇑, ↑, décrits plus loin dans cet article.
Propriétés requises[modifier | modifier le code]
Voici quelques propriétés que l'on souhaite voir satisfaites par un système de substitutions explicites[1]. Tout d'abord il y a des propriétés requises.
- Le système doit être confluent sur les termes clos, c'est-à-dire sur les termes qui ne contiennent pas de variables libres.
- Le système doit simuler chaque étape de β-réduction.
- Le système restreint aux substitutions seules doit être fortement normalisable, c'est-à-dire que toutes les réductions qui ne contiennent pas d'élimination de β-rédex doivent se terminer.
Il y a aussi des propriétés optionnelles que l'on peut souhaiter.
- Pour définir les règles on introduit des variables ad hoc (différentes des variables internes du système et du lambda-calcul), qui peuvent être remplacées par n'importe quel terme et que l'on appelle méta-variables, formant ainsi des méta-termes. Le système devrait être confluent sur les méta-termes.
- Le système de substitutions explicites devrait permettre de composer les substitutions.
- Le système de substitutions explicites devrait préserver la forte normalisation. Cela signifie que tout terme fortement normalisable du lambda-calcul devrait rester fortement normalisable quand on l'immerge dans la calcul de substitutions explicites.
- Le système de type du lambda-calcul s'étend et conserve ses caractéristiques comme la forte normalisation des termes typables.
- Le système devrait être simple, aussi bien du point de vue du nombre d'opérateurs, que du nombre de règles, de leur complexité et de leurs conditions annexes.
Variantes[modifier | modifier le code]
Il y a plusieurs calculs de substitutions explicites. Cela peut s'expliquer de deux façons :
- il y a différentes sortes de syntaxe: avec des variables explicites ou des variables implicites, avec des opérateurs différents,
- certaines propriétés citées plus haut sont satisfaites par un système et pas par un autre. Un système de substitutions explicites fait un compromis entre ces propriétés.
En général, les systèmes qui sont confluents sur les méta-termes ne préservent pas la forte normalisation et vice-versa. Ceux qui satisfont ces deux propriétés ne sont pas simples.
Le calcul λx[modifier | modifier le code]
Le système λx utilise des noms explicites de variables et comporte quatre règles pour le système de substitutions, plus une règle pour éliminer les β-rédex et ainsi simuler la β-réduction.
- (b) : (λx.M) N → M⟨x:=N⟩
- (xvI) : x⟨x:=P⟩ → P
- (xvK) : x⟨y:=P⟩ → x (x≠y)
- (xap) : (M N) ⟨x:=P⟩ → (M⟨x:=P⟩) (N⟨x:=P⟩)
- (xab) : (λx.M) ⟨y:=P⟩ → λx.(M⟨y:=P⟩) (x≠y)
Le système λx préserve la forte normalisation. On peut y ajouter la règle suivante qui généralise et donc remplace la règle (xvK).
- (xgc) : M⟨x:=P⟩ → M (x∉var(M))
Présentation des règles[modifier | modifier le code]
- La règle (b) élimine un β-rédex et introduit une substitution explicite.
- Dans la règle (xvI), le membre gauche est formé d'une substitution affectée à une variable. Comme la variable en question est la même que la variable de la substitution, on élimine la substitution en retournant le corps de celle-ci.
- La règle (xvK) a aussi un membre gauche formé d'une substitution affectée à une variable, mais comme les variables sont différentes, on retourne la variable.
- La règle (xap) distribue une substitution dans une application. Une bonne implantation devrait faire un partage.
- La règle (xab) fait entrer une substitution dans une abstraction.
- La règle (xvgc) évoque le glanage de cellules, d'où les deux lettres g et c. Là aussi le membre gauche est formé d'une substitution affectée à un terme qui ne contient pas la variable. On élimine la substitution en la supprimant, ce qui fait disparaître le corps de la substitution et équivaut à une récupération de mémoire c'est-à-dire un glanage de cellules.
Le calcul λυ[modifier | modifier le code]
Le calcul λυ utilise des indices de de Bruijn. Il n'y a donc plus de variables, mais seulement des méta-variables. Ne contenant plus de variables liées, λυ est un système de réécriture du premier ordre. Les ajouts syntaxiques sont les suivants.
- La substitution [N/] dit que dans le terme auquel elle est affectée, l'indice 0 doit être remplacé par N (règle (FVar)). Mais comme on supprime alors le 0, on doit aussi décrémenter les autres indices (règle (RVar)).
- L'opérateur de hissage (Lift en anglais), noté ⇑, modifie une substitution. Il prend en compte le fait que la substitution apparaît sous un λ. Il laisse donc inchangé l'indice 0 (règle (FVarLift)) et attache à chaque autre indice un terme dont les indices qu'il contient sont incrémentés par la substitution décalage (règle (RVarLift)). Sur les indices cela fonctionne comme suit:
- ⇑(s) : 0 ↦ 0
- 1 ↦ s(0) [↑]
- 2 ↦ s(1) [↑]
- ⁞
- n+1 ↦ s(n) [↑]
- ⁞
- ⇑(s) : 0 ↦ 0
- La substitution de décalage (Shift en anglais), notée ↑, incrémente les indices d'un terme (règle (VarShift)).
- (B) : (λ M) N → M [N/]
- (App) : (M N)[s] → M[s] N[s]
- (Lambda) : (λ M)[s] → λ (M[⇑(s)])
- (FVar) : 0[M/] → M
- (RVar) : n+1[M/] → n
- (FVarLift) : 0[⇑(s)] → 0
- (RVarLift) : n+1[⇑(s)] → n[s][↑]
- (VarShift) : n[↑] → n+1
Le calcul λυ préserve la forte normalisation.
Présentation des règles[modifier | modifier le code]
Les trois premières règles correspondent aux règles équivalentes de lambda-x, par exemple, la règle (B) élimine un bêta-rédex et introduit une substitution explicite.
- La règle (FVar) a pour terme l'indice 0 et pour partie substitution M/, elle retourne M.
- La règle (RVar) a pour terme l'indice n+1 et pour partie substitution M/, elle décrémente l'indice et oublie M. Pour justifier cette règle, il faut se souvenir que n+1 vient de dessous un lambda qui a disparu.
- La règle (FVarLift) met en face à face un indice 0 et une opération de hissage. 0 est inchangé par le hissage.
- La règle (RVarLift) prend en compte le fait suivant : si on applique le hissage d'une substitution à un indice strictement positif on obtient un terme résultant de l'application de la substitution à l'indice précédent dans lequel tous les indices internes sont décalés, c'est-à-dire incrémentés. On notera que dans le membre droit de ce terme il y a deux applications successives de substitutions : à savoir la substitution hissée et le décalage.
- La règle (VarShift) réalise le décalage ou incrémentation.
Le calcul λσ[modifier | modifier le code]
Le calcul λσ est le calcul originel d'Abadi, Cardelli, Curien et Lévy[2]. En plus des opérateurs du calcul λυ, ce calcul possède
- une constante id pour noter la substitution identité,
- un opérateur · pour ajouter un terme en tête d'une substitution et
- un opérateur de composition ∘ .
Il n'y a pas d'opérateur ⇑, ni de substitution M/.
| (Beta) | (λ M) N → M [N · id] |
|---|---|
| (App) | (M N)[s] → M[s] N[s] |
| (Abs) | (λ M)[s] → λ (M[0 · (s ∘ ↑)]) |
| (Clos) | M[s][t] → M[s ∘ t] |
| (VarId) | 0 [Id] → 0 |
| (VarCons) | 0 [M.s] → M |
| (IdL) | id ∘ s → s |
| (ShiftId) | ↑ ∘ id → ↑ |
| (ShiftCons) | ↑ ∘ (M . s) → s |
| (AssEnv) | (s ∘ t) ∘ u → s ∘ (t ∘ u) |
| (MapEnv) | (M . s) ∘ t → M[t] . (s ∘ t) |
Alors que les substitutions de λυ disent quoi affecter à l'indice 0 et à ses avatars quand il s'enfoncent dans les λ et comment décaler les indices autres que 0, les substitutions de λσ regroupent en une seule substitution les affectations à tous les indices et pour cela elles comportent un opérateur de composition.
Histoire[modifier | modifier le code]
L'idée de la substitution explicite est esquissée dans la préface du livre[3] de Curry et Feys sur la logique combinatoire, mais acquiert le statut d'un véritable système de réécriture de termes dans les travaux que conduit de Bruijn[4] en connexion avec le système Automath. En revanche, le concept et la terminologie sont habituellement crédités à Martín Abadi, Luca Cardelli, Curien et Lévy. Dans un article[2] qui sera le premier d'une grande lignée, les auteurs introduisent le calcul λσ et montrent que le lambda-calcul doit être étudié avec beaucoup d'attention en ce qui concerne la substitution. Sans des mécanismes sophistiqués de partage de structure, les substitutions peuvent exploser en taille.
Notes et références[modifier | modifier le code]
- Delia Kesner: A Theory of Explicit Substitutions with Safe and Full Composition. Logical Methods in Computer Science 5(3) (2009)
- M. Abadi, L. Cardelli, P-L. Curien and J-J. Levy, Explicit Substitutions, Journal of Functional Programming 1, 4 (October 1991), 375–416.
- (en) Haskell Curry et Robert Feys, Combinatory Logic Volume I, Amsterdam, North-Holland Publishing Company,
- N. G. de Bruijn: A namefree lambda calculus with facilities for internal definition of expressions and segments. Technological University Eindhoven, Netherlands, Department of Mathematics, (1978), (TH-Report), Number 78-WSK-03.
Bibliographie[modifier | modifier le code]
- Kristoffer Høgsbro Rose, Roel Bloo, Frédéric Lang: On Explicit Substitution with Names. J. Autom. Reasoning 49(2): 275-300 (2012)
- N. G. de Bruijn: A namefree lambda calculus with facilities for internal definition of expressions and segments. Technological University Eindhoven, Netherlands, Department of Mathematics, (1978), (TH-Report), Number 78-WSK-03.
- Martín Abadi, Luca Cardelli, Pierre-Louis Curien et Jean-Jacques Lévy, « Explicit Substitutions », J. Funct. Program, vol. 1, no 4, , p. 375-416
- Delia Kesner: A Theory of Explicit Substitutions with Safe and Full Composition. Logical Methods in Computer Science 5(3) (2009)
- Zine-El-Abidine Benaissa, Daniel Briaud, Pierre Lescanne, Jocelyne Rouyer-Degli: λυ, A Calculus of Explicit Substitutions which Preserves Strong Normalisation. J. Funct. Program. 6(5): 699-722 (1996); Version en ligne.
- Pierre Lescanne: From Lambda-sigma to Lambda-upsilon a Journey Through Calculi of Explicit Substitutions. POPL 1994: 60-69
Voir aussi[modifier | modifier le code]
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Explicit substitution » (voir la liste des auteurs).


 French
French Deutsch
Deutsch