Méridienne (géodésie) — Wikipédia

Une méridienne est un arc de méridien déterminé par triangulation géodésique et mesures astronomiques. Une de ses finalités premières est de déterminer la grandeur d'un degré de méridien terrestre, en un lieu, pour « mesurer la Terre^[1] ».

La détermination, à l'origine, de la grandeur d'un arc de méridien passe par trois phases qui sont :

1. la triangulation sur une zone géographique retenue ;
2. la recherche de la direction du méridien en un des lieux triangulés, suivie de la projection des triangles sur cette méridienne ;
3. la détermination de la différence de latitude des points extrêmes de la triangulation pour en déduire un degré de méridien.

La recherche géodésique des dimensions de la Terre date du début du XVII^e siècle. Elle donne lieu à de nombreuses méridiennes fondamentales, jusqu'à la fin du XVIII^e siècle, pour valider ou non certaines hypothèses sur la forme de la Terre.

Conjointement à la mesure de la Terre, les méridiennes vont servir, le plus souvent, au développement d'un maillage de triangulations secondaires pour une nouvelle cartographie géométrique, telle la carte de France des Cassini.

Détermination d'une méridienne[modifier | modifier le code]

Triangulation[modifier | modifier le code]

Le principe de triangulation d'une méridienne s'appuie sur la triangulation élémentaire (voir figure) : à partir d'un premier triangle-plan ABC, dont on mesure un côté - la base AB - et les angles^{[N 1]}, on peut, trigonométriquement, déterminer les deux autres côtés. Ce premier triangle défini, on détermine, à partir de l'un de ses côtés (ici BC), un deuxième triangle adjacent BCD et, de proche en proche, un réseau de triangles dont les sommets sur le terrain, sont situés, au mieux, de part et d'autre de l'arc de méridien à mesurer^[2].

Mesure de la base[modifier | modifier le code]

La base est choisie sur un terrain le plus plat possible et de longueur maximum. La mesure s'effectue avec des perches mises bout à bout, sur toute la longueur de la base.

Optimisation : La base doit être la plus longue possible (plusieurs kilomètres) pour accroitre la précision des calculs de triangulation ; les perches, dont la fabrication va évoluer au cours des XVII^e et XVIII^e siècles se doivent d'être d'une longueur rattachée à un étalon de référence. Pour éviter les incertitudes d'une mesure unique, plusieurs mesurages, indépendants et menés en parallèle sont souhaitables.

Mesure des triangles[modifier | modifier le code]

L'instrument de mesure des angles, pendant les deux siècles concernés, est principalement le quart de cercle mobile. Il va évoluer et son exactitude ira en s'améliorant.

Optimisation : Le triangle idéal est le triangle équilatéral (3 angles à 60°) ; les triangles avec un angle aigu sont à bannir, les erreurs engendrées sur les longueurs étant très importantes. Les mesures de chaque angle doivent être au minimum doublées pour réduire l'incertitude angulaire. Les propriétés des triangles et des polygones sont à exploiter au maximum :

• les trois angles d'un triangle font 180°, il est intéressant de mesurer chacun des trois angles et de comparer leur somme aux 180° théoriques ;
• en un sommet particulier, il est souhaitable de faire un tour d'horizon de tous les angles balayés, la somme devant faire 360°^{[N 2]} ;
• la chaîne de triangles forme un polygone à n côtés. La somme des angles de ce polygone est de 180 (n-2) degrés. Soit pour la figure un nonagone (9 côtés) dont la somme des angles doit valoir 180 x 7 = 1260°
• il est parfois nécessaire de tracer des liaisons supplémentaires entre sommets pour vérifier certains angles sur lesquels il peut y avoir doute (par exemple DG).

« Pour s'assurer de l'exactitude des résultats obtenus, on mesure un côté des derniers triangles qui devient une base de vérification^[3]». Sur la figure, HI pourrait être théoriquement une base de vérification, mais, bien souvent, le terrain ne se prête guère à l'opération.

Pour finir, si les différents plans des relevés angulaires ne sont pas horizontaux, il est souhaitable de projeter ou « réduire » les triangles dans un plan horizontal.

Recherche d'un méridien de référence[modifier | modifier le code]

En un point choisi de la triangulation (ici, au point extrême en I), on va déterminer la direction du méridien par des méthodes astronomiques connues. L'instrument privilégié reste toujours le quart de cercle.

Parmi les méthodes astronomiques employées, on peut citer :

• la méthode basée sur la mesure des hauteurs correspondantes d'un astre (soleil, étoile) ;
• une méthode liée à l'observation de la Polaire à sa plus grande digression.

La matérialisation de la méridienne sur le terrain est réalisée par des mires éloignées du point de mesure. Elles vont permettre de mesurer l'angle d'azimut d'un côté du dernier triangle de la chaîne (ici α = HI-X1X2).

Il restera ensuite à projeter trigonométriquement la triangulation sur la méridienne, ce qui donnera la longueur de l'arc de la méridienne X1X2^[4].

Détermination d'un degré de latitude[modifier | modifier le code]

On mesure, aux deux points extrêmes de la triangulation A et I, la distance zénithale d'une étoile connue. Le mesurage s'effectue avec un secteur qui est un instrument adapté à l'opération. La différence entre les deux mesures donnera la différence de latitude entre les deux points.

Optimisation : La mesure de la différence des latitudes doit être très exacte ; c'est le facteur primordial d'un bon résultat. C'est pour cela que le secteur est un instrument de grand rayon, avec une bonne résolution. Pour réduire encore l'incertitude de mesurage, il est souhaitable d'effectuer, à chaque station (A et I), des mesures par retournement de l'instrument. Il est aussi nécessaire d'effectuer les mesures aux deux extrémités dans des temps très rapprochés ; ceci pour éviter les effets de l'aberration, phénomène découvert par Bradley, vers les années 1730.

À ce stade, il ne reste plus qu'à calculer la longueur d'un degré de méridien en divisant la longueur de l'arc projeté par l'angle correspondant à la différence des latitudes concernées^[5].

Pour conclure, dans la réalité des mesurages, des éléments extérieurs vont faire que l'optimisation est plus ou moins respectée. Les principaux points de non-respect et leurs conséquences seront précisés, si possible, pour chaque méridienne étudiée.

La méridienne de Snellius[modifier | modifier le code]

Au XVII^e siècle, la Terre est supposée sphérique et, c'est en 1614 que Snellius mesure, pour la première fois par triangulation, un arc de méridien^[6] aux Pays-Bas, entre Alkmaar et Berg op Zoom^[7], essentiellement dans un but cartographique. Son instrument principal est un quart de cercle mobile ; il est à alidade et pinnules, et sa résolution est d'une minute de degré.

Triangulation auxiliaire[modifier | modifier le code]

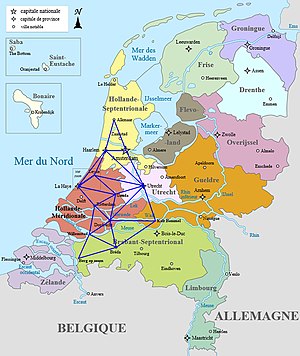
Dans un premier temps, Snellius effectue une triangulation auxiliaire (voir zoom) dont la finalité est de calculer une pseudo-base - non mesurée - de Leyde à La Haye, pour sa triangulation principale.

Cette triangulation auxiliaire est composée de 14 triangles. Entre Leyde et Zoeterwoude, il mesure une base tc = 85,05 perches (319,8 m)^{[N 3]}. Par triangulation, il calcule et mesure ensuite une première base de vérification ae ; par le calcul, il trouve ae = 326,43 p, et plusieurs mesurages lui donnent une valeur moyenne de 326,90 p^[8]. Il s'en tient à la valeur calculée « et l'erreur sur ae est déjà d'une demi-perche environ, ou 1/600.» Partant de cette nouvelle base, il calcule la distance entre Leyde et Zoeterwoude LZ = 1092,33 p, puis de proche en proche, il parvient à déterminer la distance de Wassenaar à Voorschoten qu'il vérifie par la mesure d'une nouvelle base ai qui correspond au calcul au centième de perche près^[9]. Il termine par la distance Leyde - La Haye LH = 4103,36 p, qu'il vérifie à 0,15 p près par un triangle auxiliaire LHZ.

Triangulation principale[modifier | modifier le code]

LH va servir de référence à la mesure du degré dans la triangulation principale. À ce stade de la description volontairement détaillée, Delambre^[10] précise que les angles sont souvent petits et que seuls deux angles sur trois sont mesurés. Pour conclure il ajoute « Il faut avouer que ces préliminaires sont un peu entortillés, et les bases bien petites ; mais du moins l'auteur a eu soin de donner plusieurs vérifications, qui diminueront un peu l'incertitude^{[N 4]}. »

La triangulation principale est effectuée au quart de cercle ou avec un demi-cercle (graphomètre ?) de 3,5 pieds de diamètre (55 cm de rayon) dont on ne connait pas la division. Elle comporte une quinzaine de triangles essentiels et une autre quinzaine qui servent à la vérification et à la simplification des calculs effectués sans table de logarithmes. Seuls 10 triangles sont mesurés sur les trois angles. Les 180° de ces 10 triangles varient entre -1° et 4°. La longueur moyenne des côtés des triangles principaux vaut environ 29 km.

« Pour orienter son réseau, Snellius trace une méridienne à Leyde, et il observe, sans en donner la méthode, l'azimut de Gouda ; [il en déduit l'angle de la méridienne avec] Leyde-Alkmaar, soit φ-Leyde-Alkmaar = 15° 28′. » Ses triangles, réduits sur la méridienne donnent un arc de 33 930,2 perches.

Pour terminer, Snellius mesure la hauteur du pôle, avec un quart de cercle de 5,5 pieds de rayon (≈ 1,7 m) à Leyde et aux extrémités de sa triangulation ; il en déduit l'amplitude de l'arc de méridien : 1° 11′ 30″. Il ne lui reste plus qu'à déterminer l'amplitude du degré : 28 473 perches ; il s'arrêtera à 28 500 perches du Rhin, soit 107 160 m^{[N 5],[11]}.

Snellius reprendra ses calculs par deux fois ; puis près d'un siècle après, Musschenbroek corrigera certains calculs, notamment sur la hauteur du pôle aux extrémités. Il en conclut une amplitude de l'arc de méridien de 1° 9′ 47″ d'où une valeur du degré terrestre de 29 514,2 perches du Rhin, soit 110 973 m.

Delambre souligne cette différence d'amplitude (1′ 43″) et constate que la principale erreur de Snellius provenait des relevés des latitudes « et que les erreurs géodésiques étaient peu de choses en comparaison »^[12]. Après quelques reproches : « avoir si souvent conclu le troisième angle [de ses triangles], avoir mêlé à des triangles bien conditionnés des triangles trop obtus, et surtout avoir employé de trop petites bases », Delambre reconnait la qualité des travaux de Snellius : « si l'on songe qu'il n'avait que des pinnules, on concevra une idée assez favorable de ses instruments et de sa manière d'observer… ».

La méridienne de Picard[modifier | modifier le code]

En 1669, en France, l'abbé Picard va être amené à mesurer un degré de méridien^[13], dans le but défini par Colbert de cartographier la France de façon géométrique ; la région « prototype » est la région parisienne, l'emplacement de la méridienne se trouve à l'est de Paris, entre Malvoisine^{[N 6]} et Sourdon-Amiens. C'est l'abbé qui, le premier, va adapter des « lunettes d'approche, au lieu des pinnules, sur ses instruments : quart de cercle et secteur, avec une bien plus grande justesse que celle que l'on avait jusqu'alors^[14]». Pour faire ses mesures, l'abbé Picard va se servir de la toute nouvelle toise du Châtelet, que Colbert imposera alors par décret national dès 1668. Elle sera de 5‰ (0,5%) plus courte que l'ancienne toise du Châtelet qui valait 1,959576 m. Elle vaudra dorénavant (et ce jusqu'en 1766 où elle sera à son tour remplacée par « la toise du Pérou ») : 1,94977812 m^{[réf. nécessaire]}. La toise valant elle-même, par définition, invariablement 6 pieds de Roy (de France), le « pied de Roy » (qui sert d'étalon de référence), subit lui aussi une identique « dévaluation », passant de 0,326596 m à 0,324963 m.

Les triangles[modifier | modifier le code]

À l'origine, il choisit treize stations^[15] (du point A au point N sur la figure) pour construire treize grands triangles, mais il commence par mesurer une base AB entre le moulin de Villejuif jusqu'au pavillon de Juvisy : « On prit quatre bâtons de pique, bien droits, que l'on assembla deux à deux ; & on les coupa de quatre toises (≈ 7,8 m)^{[N 7]} de longueur chacune. Les extrémités en étaient garnies de plaques de cuivre, pour que l'on pût les appliquer l'un au bout de l'autre, le long d'un grand cordeau bien tendu, en s'alignant à chaque fois qu'on le changeait de place, aux deux termes de cette base ; en sorte que l'on relevait un de ces bâtons, pendant que l'autre demeurait immobile à terre ; auquel on le rappliquait par l'autre bout en avançant toujours dans le même alignement. ». Deux mesurages donnent alors 5 662 toises 5 pieds et 5 663 toises 1 pied. Soit 5 663 toises ± 1 pied^{[N 8]} ; C'est cette valeur moyenne (≈ 11 026 m) qui sera retenue.

Sur les treize triangles principaux, dont les côtés valent en moyenne environ 28 km, il mesure les trois angles sur neuf triangles. Après réduction au plan horizontal, les angles sont corrigés pour fermer les triangles à 180° ; il ne donne guère les écarts sur les 180° théoriques sauf pour un triangle où il manque 10″. D'après Levallois^[16], la dispersion sur les mesures serait de l'ordre de ±20″. Picard précise aussi qu'en station :

• « sur un tour d'horizon pris en cinq ou six angles, on n'a jamais trouvé qu'environ une minute de plus ou de moins qu'il ne fallait », et que souvent l'erreur ne dépassait pas 5″.
• que les observations sont réitérées deux ou trois fois, avec des observateurs différents qui ne se communiquaient leurs résultats qu'en final.

Pour s'assurer de ses calculs, il s'appuiera sur des triangles auxiliaires et, pour les quatre triangles où il ne mesure que deux angles (accès impossible aux clochers par exemple), il va mesurer par deux fois, vers le point M, une base secondaire transversale XY de 3902 toises qu'il confronte à ses calculs.

Réduction sur la méridienne[modifier | modifier le code]

Pour déterminer l'orientation de sa triangulation par rapport au méridien, il détermine, en fait, deux méridiennes : l'une à Mareil et l'autre à Sourdon qui deviendra référence. Il emploie son quart de cercle dans le plan vertical et s'appuie sur la plus grande digression de l'étoile polaire ; il détaille la méthode : repérage du vertical de l'étoile avec une lunette, pointage sur l'horizon de ce vertical avec le filet de l'autre lunette… Il réitère plusieurs fois cette opération pour s'en assurer et oriente ensuite un côté particulier de sa triangulation. À Sourdon, il trouve que la ligne Sourdon-Clermont décline du Midi vers l'Orient de 2° 9′ 10″.

La projection sur la méridienne de ses triangles lui donne, entre Sourdon et Malvoisine, un arc de 68 347 toises 3 pieds (≈ 133 263 m)^[17].

Détermination du degré[modifier | modifier le code]

L'abbé va déterminer la différence de latitude, entre Malvoisine et Sourdon, avec un secteur de 10 pieds de rayon, qu'il appelle ici Portion de cercle. L'étoile de référence est dans le genou de Cassiopée (δ Cassiopei) qu'il observe après avoir vérifié par retournement son instrument. Il effectue de nombreuses mesures dont la variation n'excède pas 5″. Tous calculs et corrections faits, la différence de latitude entre Malvoisine et Sourdon est de 1° 11′ 57″.

Il en conclut que le degré du méridien terrestre contient 57 064 toises 3 pieds^{[N 9]}, mais une autre observation faite à Amiens, par le moyen de quelques triangles (MRT & NTX)^{[N 10]} lui fera décider de choisir la grandeur du degré « de 57 060 toises picard (111 255 m), qui prises 360 fois donneront la circonférence entière du Méridien terrestre, si la Terre est réellement d'une figure sphérique, comme on le suppose ici. », soit 20 541 600 toises ou 40 051,6 km pour fixer les idées. Sa rigueur lui fait dire :

• que sa triangulation n'étant pas réalisée au niveau de la mer, la circonférence de la Terre en serait affectée. Il calcule alors la correction à effectuer en fonction de l'altitude, et il ne trouve que huit pieds à retrancher au degré ; il s'en tient alors à son résultat.
• qu'il demeure une incertitude qu'il estime à plus de 60 toises (117 m) au degré, ce qui donne une incertitude de 42 km sur la circonférence terrestre ; il suggère alors de prolonger la méridienne sur plusieurs degrés, ce que le Roi ordonnera en 1683^[18].

La méridienne de Jean Picard, référence géodésique européenne, sera reprise en partie par J. Cassini, Maupertuis, La Caille, Delambre, etc. pour valider certaines hypothèses la concernant.

La méridienne de Paris[modifier | modifier le code]

En 1683, « Sa Majesté ordonne aux Mathématiciens de l'Académie des Sciences de continuer l'entreprise [de Picard] et de prolonger vers le Septentrion & vers le Midi jusques aux confins du Royaume, une Ligne Méridienne qui passât par le milieu de l'Observatoire de Paris^[19]. »

Dès 1683, donc, les travaux débutent : J.-D. Cassini, chargé des opérations, se dirige vers le Sud et de La Hire part vers le Nord. Après la mort de Colbert (septembre 1683), les travaux s'arrêtent, reprennent en 1700-1701, avec, pour aider son père la participation de Jacques Cassini ; ils s'arrêtent de nouveau pour n'être repris et terminés qu'en 1718 par Jacques Cassini, Maraldi et le fils de La Hire^[20].

Triangulation[modifier | modifier le code]

La méridienne de Paris dite aussi méridienne des Cassini joint Dunkerque au nord, au Canigou, près de Perpignan et de Collioure, au sud en passant par le centre de l'Observatoire de Paris.

La partie sud, de l'Observatoire au Roussillon, comporte vingt-quatre triangles principaux. La partie nord, de l'Observatoire à Dunkerque en comporte trente, soit au total cinquante-quatre triangles qui décrivent un arc de 8,5° de latitude, soit plus de huit fois la grandeur de l'arc de Picard. Les triangles sont réduits au niveau de la mer, mais on constate que la conformation des triangles est souvent médiocre, surtout dans la partie sud, à partir de Bourges : mesure de petits angles, avec de nombreux angles conclus. La chaîne complète s'appuie sur trois bases :

• la base de Dunkerque de 5 564 toises ;
• la base de Villejuif (de Picard) de 5 663 toises ;
• la base de Leucate de 7 246 toises.

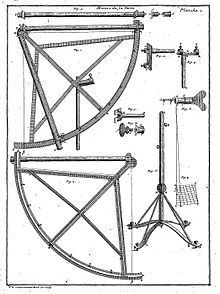
Les triangles sont mesurés au quart de cercle. Les bases le sont probablement par des règles constituées de quatre bois de piques de deux toises chacun, règles étalonnés avec une règle de fer de quatre pieds portée exprès de Paris. La description n'est détaillée que pour la base de Leucate ; il est supposé que la toise Cassini est la même que la toise Picard^[21].

Direction du méridien de Paris[modifier | modifier le code]

La direction du méridien de référence passe par le centre de l'Observatoire. En 1683, Cassini I^er et La Hire affinent la localisation de la Mire du Nord de la méridienne mise en place par Picard. Corrigée de deux pieds, elle sera dès lors la référence primaire de la ligne méridienne^[22].

D'autres mesures sont effectuées en différents points de la triangulation au quart de cercle (Sermur, Montlhéry, Rodez, Perpignan…) pour validation. Les méthodes employées sont évoquées, sans plus de précisions : observation de l'azimut du soleil à son lever et à son coucher, méthode des hauteurs correspondantes. L'exactitude n'est pas parfaite. D'après Delambre il y aurait des erreurs de 17, 38, 9, 27 secondes de degré en différentes stations, mais comme il le dit « tout cela est peu dangereux^[23] ».

Pour la carte de France, la méridienne apporte des améliorations considérables. Avant son tracé, il était supposé que Paris était sur le même méridien que Montpellier. La nouvelle carte de France, « où sont marqués les triangles qui ont servi à déterminer la Méridienne de Paris » scellera le fait qu'à partir de 1718 le méridien de Paris passe par la ville de Carcassonne.

Détermination des degrés de latitude[modifier | modifier le code]

Les stations astronomiques principales sont à Dunkerque, Paris et Collioure.

La détermination de l'amplitude des arcs de latitude, en ces trois stations, s'effectue au secteur astronomique. Cassini II emploie deux secteurs différents : le premier, qui lui est propre, sert aux stations de Collioure et à l'Observatoire et, le second, identique à celui de Picard, est utilisé à Paris et à Dunkerque. Il observe des distances zénithales de différentes étoiles passant au méridien (essentiellement γ Dragon). Il précise qu'il effectue ses mesures aux stations correspondantes à la même époque de l'année pour éviter des variations saisonnières des étoiles, variations non maîtrisées à cette époque. Delambre ne fait pas confiance aux mesures effectuées avec le premier secteur aux stations de Collioure et de l'Observatoire^[24].

Finalement, pour les trois stations ci-dessus, Cassini note :

• Dunkerque : φ = 48° 50′ 10″ + 2° 1215,5′ = 51° 02′ 25,5″ ;
• Paris : 48° 50′ 10″ ;
• Collioure : 48° 50′ 10″ - 6° 18′ 56″ = 42° 31′ 14″.

Après projection sur la méridienne, il annonce pour le degré de méridien les résultats suivants :

• Paris-Collioure : 57 097 toises au degré ;
• Paris-Dunkerque : 56 960 toises au degré ;
• Soit 57 061 toises (i.e. 111,256 km) au degré pour la sphère moyenne.

Il en conclut donc en bon cartésien « il rait avec assez d'évidence que les degrés d'un méridien sont plus grands plus ils sont près de l'Équateur et diminuent au contraire à mesure qu'ils s'approchent du pôle. »

« Cette affirmation fut le départ d'une célèbre controverse scientifique qui durera quinze ans, sera tranchée par Maupertuis en 1737 et dont sa méridienne fera les frais. »^[25].

La méridienne au cercle polaire[modifier | modifier le code]

Depuis les résultats de J. Cassini, en 1718, la polémique sur la forme de la Terre fait rage entre partisans de l'école « ancienne » des cartésiens représentés par Cassini lui-même et l'école « moderne » qui suit Huygens et Newton. C'est dans ce contexte que se mettent en place des expéditions géodésiques françaises, l'une vers l'Équateur dirigée sur le papier par Louis Godin, l'autre au Nord dirigée par Maupertuis, fervent partisan de Newton.

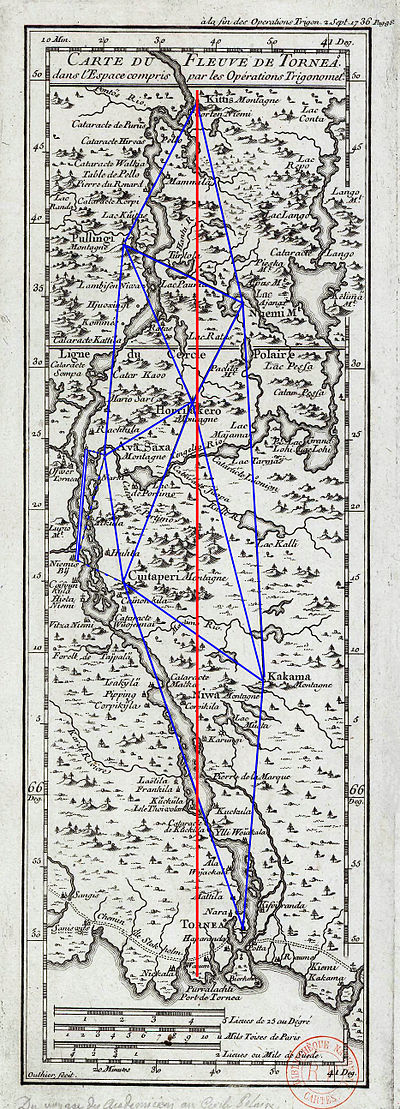
L'expédition au Nord, sera organisée en 1736 et prendra la direction du fond du golfe de Botnie, en Laponie, entre Suède et Finlande, vers le cercle polaire.

Triangulation[modifier | modifier le code]

La chaîne s'étend sur environ 100 km, elle comporte neuf sommets principaux établis entre Tornea au sud et Kittis au nord. Une base lui est rattachée au milieu de la chaîne, vers Avasaxa Les triangles sont déterminés avec un quart de cercle de deux pieds de rayon disposant d'un micromètre. Les trois angles sont toujours observés et le plus petit angle est de 31° sur les triangles principaux. La dispersion des mesures angulaires tirées des fermetures des triangles est de ±12″. L'erreur sur un tour d'horizon de 180° est de 8.6″, soit 6′ sur chaque angle, ou mieux de 5″ en tenant compte de l'excès sphérique. Les triangles observés forment un heptagone (sept côtés) dont la somme des angles vaut théoriquement 900°; elle est supérieure de 1′ 37″ et Delambre estime que l'erreur sur les seize angles entrant en ligne de compte est de 64″, soit une erreur moyenne de 4″ par excès pour chaque angle.

La base est mesurée dans des conditions difficiles sur le fleuve gelé de Tornea, à la fin du mois de décembre et par une température voisinant les -25 °C. Le mesurage est effectué par deux équipes en parallèle, à l'aide de perches de bois, de cinq toises de longueur, cloutées aux extrémités. Le détail des opérations est connu grâce au journal de l'abbé Outhier. Le résultat final est de 7 406,86 toises (environ 14 436 m) avec une écart entre les mesures des deux équipes de quatre pouces, soit moins de onze centimètres.

La méridienne[modifier | modifier le code]

La direction de la méridienne est déterminée en premier sur la montagne de Kittis, point extrême nord de la triangulation. On y construit deux observatoires, le plus petit servant à abriter une pendule et une petite lunette méridienne de vingt pouces employée, à cet usage, pour la première fois par Le Monnier. Par la méthode des hauteurs correspondantes du Soleil, on va déterminer le temps de midi à la pendule et prendre la direction du Soleil en cet instant, avec la lunette placée précisément à la pointe du dernier triangle. Abaissée verticalement, elle donne un point à l'horizon qui servira à déterminer, à de nombreuses reprises, les azimuts des signaux de Pullingi et de Niemi. La direction de la méridienne est « tracée », des opérations similaires seront effectuées à Tornea. Il sera constaté des écarts d'azimut allant jusqu'à 34.5″, mais ceux-ci n'ont guère d'incidence sur la longueur de l'arc de méridien à mesurer.

Détermination du degré[modifier | modifier le code]

À Kittis, le grand observatoire, lui, va recevoir le secteur de Graham et une pendule pour les observations astronomiques.

Y sont observées les distance zénithales de δ Draconis et de α Draconis, plusieurs jours de suite, en deux campagnes différentes. Les mêmes observations auront lieu à Tornea dans les mêmes conditions, à quelques jours près. Dans ces observations, il est tenu compte de la précession, de l'aberration et de la nutation communiquées à Maupertuis par Bradley.

Le seul fait qui sera reproché à Maupertuis, notamment par Delambre, dans cette opération, est qu'il ait négligé d'effectuer des mesures, par retournement, au secteur.

Au résultat final l'arc évalué par les deux mesurages aux extrémités de la chaîne donne :

- pour δ du Dragon : 57′ 26,9″ - pour α du Dragon : 57′ 30,4″

soit une moyenne de 57′ 28,7″ Maupertuis en déduit un degré de méridien de 57 438 toises (du Nord) à la latitude moyenne de 66° 20′ (résultat à comparer aux 57 060 toises (Picard) déterminées par Jean Picard, vers Paris, à 48° de latitude).

Conforté par les observations pendulaires effectuées à Paris et en Laponie, non développées ici, Maupertuis peut donc affirmer, à son retour à Paris, que la Terre est bien un sphéroïde aplati aux pôles, conformément aux idées d'Huygens et de Newton. Ce résultat scientifique fondamental va avoir un profond retentissement, et Jacques Cassini n'admettra jamais qu'il ait pu se tromper dans sa détermination de la Méridienne de Paris^[26].

Galerie[modifier | modifier le code]

• 
  Détail du plan de Tornea avec l'église au centre.
• 
  L'église de Tornea, point géodésique sud.
• 
  Le signal de Niemi, en construction.
• 
  Kittis : détail montrant les deux observatoires.
• 
  Vers Kittis, détail du plan de Pello.

• 
  Hommage à l'expédition de Maupertuis.
• 
  Cataracte de Kattila sur le Torne, au cercle polaire.
• 
  Pello, au pied de Kittis.
• 
  Monument à Aavasaksa, vers le terme nord de la base.
• 
  Une église luthérienne typique à Tornio.

Autres méridiennes historiques[modifier | modifier le code]

• La méridienne vers l'équateur ;
• La méridienne du Cap ;
• La méridienne de France.

Notes et références[modifier | modifier le code]

Notes[modifier | modifier le code]

Références[modifier | modifier le code]

Annexes[modifier | modifier le code]

Bibliographie[modifier | modifier le code]

Jean-Jacques Levallois, Mesurer la Terre : 300 ans de géodésie française, Paris, A.F.T., 1988, 389 p. (ISBN 2-907586-00-9).

J.-B. Delambre, Histoire de l'astronomie moderne, t. 1, Paris, Coursier, 1821 (lire en ligne).

J.-B. Delambre, Histoire de l'astronomie moderne, t. 2, Paris, Coursier, 1821+ (lire en ligne).

Académie des sciences (France), Histoire de l'Académie royale des sciences, Paris, recueils : 1699-1786 (lire en ligne).

Articles connexes[modifier | modifier le code]

• Figure de la Terre : nombreux liens.

Liens externes[modifier | modifier le code]

• Exposition virtuelle sur Jean Picard (2020) de la bibliothèque de l'Observatoire de Paris.

• Portail de la géodésie et de la géophysique
• Portail de l’astronomie
• Portail de la géographie