Loi normale — Wikipédia

Vous lisez un « bon article » labellisé en 2013.

Ne doit pas être confondu avec : des théorèmes et lemmes de Gauss parfois appelés lois de Gauss, les autres lois de Laplace ou les autres sens du terme Normal.

Loi normale
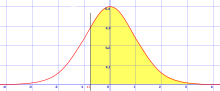
Densité de probabilité La courbe rouge représente la fonction ${\displaystyle \varphi }$, densité de probabilité de la loi normale centrée réduite.
Fonction de répartition La courbe rouge représente la fonction ${\displaystyle \Phi }$, fonction de répartition de la loi normale centrée réduite.
Paramètres	${\displaystyle \mu }$, espérance (nombre réel) ${\displaystyle \sigma ^{2}>0}$, variance (nombre réel)
Support	${\displaystyle \mathbb {R} }$
Densité de probabilité	${\displaystyle {\frac {1}{\sigma {\sqrt {2\pi }}}}\;\exp \left(-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}\right)\!~}$
Fonction de répartition	${\displaystyle {\frac {1}{2}}\left(1+\mathrm {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right)\!~}$
Espérance	${\displaystyle \mu }$
Médiane	${\displaystyle \mu }$
Mode	${\displaystyle \mu }$
Variance	${\displaystyle \sigma ^{2}}$
Asymétrie	0
Kurtosis normalisé	0
Entropie	${\displaystyle \ln \left(\sigma {\sqrt {2\,\pi \,{\rm {e}}}}\right)\!~}$
Fonction génératrice des moments	${\displaystyle \exp \left(\mu \,t+{\frac {\sigma ^{2}t^{2}}{2}}\right)}$
Fonction caractéristique	${\displaystyle \exp \left(\mu \,{\rm {i}}\,t-{\frac {\sigma ^{2}t^{2}}{2}}\right)}$
modifier

En théorie des probabilités et en statistique, les lois normales sont parmi les lois de probabilité les plus utilisées pour modéliser des phénomènes naturels issus de plusieurs événements aléatoires. Elles sont en lien avec de nombreux objets mathématiques dont le mouvement brownien, le bruit blanc gaussien ou d'autres lois de probabilité. Elles sont également appelées lois gaussiennes, lois de Gauss ou lois de Laplace-Gauss des noms de Laplace (1749-1827) et Gauss (1777-1855), deux mathématiciens, astronomes et physiciens qui les ont étudiées.

Plus formellement, une loi normale est une loi de probabilité absolument continue qui dépend de deux paramètres : son espérance, un nombre réel noté μ, et son écart type, un nombre réel positif noté σ. La densité de probabilité de la loi normale d'espérance μ et d'écart type σ est donnée par :

${\displaystyle f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\operatorname {e} ^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}}$.

La courbe de cette densité est appelée courbe de Gauss ou courbe en cloche, entre autres. C'est la représentation la plus connue de ces lois. Lorsqu'une variable aléatoire X suit une loi normale, elle est dite gaussienne ou normale et il est habituel d'utiliser la notation avec la variance σ² :

${\displaystyle X\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$.

La loi normale de moyenne nulle et d'écart type unitaire, ${\displaystyle {\mathcal {N}}(0,1)}$, est appelée loi normale centrée réduite ou loi normale standard.

Parmi les lois de probabilité, les lois normales prennent une place particulière grâce au théorème central limite. En effet, elles correspondent au comportement, sous certaines conditions, d'une suite d'expériences aléatoires similaires et indépendantes lorsque le nombre d'expériences est très élevé. Grâce à cette propriété, une loi normale permet d'approcher d'autres lois et ainsi de modéliser de nombreuses études scientifiques comme des mesures d'erreurs ou des tests statistiques, en utilisant par exemple les tables de la loi normale centrée réduite.

Définition et explications informelles[modifier | modifier le code]

Les lois de probabilité permettent de décrire de manière théorique le caractère aléatoire d'une expérience qui est considérée comme aléatoire. Les lois normales en sont des cas particuliers. La manière historique de l'aborder est par approximation^[1].

Lorsque le résultat de cette expérience aléatoire est à valeurs discrètes, par exemple la somme du lancer de deux dés vaut 2, 3… ou 12, une loi dite discrète modélise l'expérience. Les probabilités d'apparition de chaque valeur peuvent être représentées par des diagrammes en bâtons ou histogrammes (voir la figure ci-contre). Plusieurs scientifiques (voir Histoire de la loi normale) se sont intéressés à la réalisation d'un grand nombre d'expériences et au comportement de la loi de probabilité associée. Il apparaît que les fréquences d'apparition des valeurs possibles sont de plus en plus « lissées »^[2] (voir la figure ci-contre). Il existe une certaine répartition autour d'une valeur centrale ; ces probabilités peuvent être alors représentées par une courbe de Gauss ou courbe en cloche obtenue par calcul ou par expérience^[3]. Cette courbe est celle de la densité de probabilité d'une loi normale. Le rôle central de ces lois de probabilité vient du fait qu'elles sont la limite d'un grand nombre de lois de probabilité définies à partir de sommes, comme le montre le théorème central limite^[4],[5].

Une autre manière visuelle de voir apparaître cette courbe est réalisée par la planche de Galton. Des billes sont lâchées en haut de la planche ; à chaque étage, elles ont deux possibilités : aller à droite ou aller à gauche. Après plusieurs étages, elles ont donc eu plusieurs choix aléatoires. Lorsque le nombre de billes est grand, la répartition des billes suivant leur position est approximativement une loi normale^[6].

Comme pour toute loi de probabilité, plusieurs définitions équivalentes des lois normales existent : par leur densité de probabilité (la courbe de Gauss), par leur fonction de répartition, par leur fonction caractéristique, etc. Une loi normale dépend de deux paramètres : le premier donne la moyenne, c'est-à-dire la valeur « centrale » (ou « médiane ») des valeurs possibles^[7] (par exemple, la moyenne de la somme de deux dés est 7) ; le deuxième paramètre renseigne sur la dispersion des valeurs autour de cette valeur centrale^[7] : plus ce paramètre est faible, plus les valeurs proches de la valeur centrale auront une forte probabilité d'apparaître. Beaucoup de grandeurs physiques peuvent être représentées par ces deux paramètres^[8].

Lors de l'étude statistique d'une série d'observations d'une même grandeur, la moyenne des valeurs observées peut être considérée comme une aléatoire suivant une loi normale. La moyenne de cette loi normale est alors considérée comme la valeur « réelle » de la grandeur observée, et la dispersion de la loi renseigne sur l'« erreur » d'observation^[9]. C'est-à-dire qu'il est possible de calculer^[9] une valeur approchée de la probabilité qu'une variable suivant une loi normale soit dans un intervalle [μ – σ, μ + σ] autour de la moyenne μ. Il s'agit de pouvoir obtenir une approximation de la grandeur observée dans l'expérience en considérant les erreurs dues aux instruments de mesure ou autres^[2].

Histoire[modifier | modifier le code]

Le théorème central limite, Pierre-Simon de Laplace, Essai sur la philosophie des probabilités, 1840, 6^e éd., p. 90

Une des premières apparitions d'une loi normale est due^{[a 1]} à Abraham de Moivre en 1733 en approfondissant l'étude de la factorielle n! lors de l'étude d'un jeu de pile ou face. Il publie The Doctrine of Chances en 1756 dans lequel une loi normale apparaît comme limite d'une loi binomiale, ce qui sera à l'origine du théorème central limite^{[a 2]}. En 1777, Pierre-Simon de Laplace reprend ces travaux et obtient une bonne approximation de l'erreur entre cette loi normale et une loi binomiale grâce à la fonction gamma d'Euler^{[a 1]}. Dans son ouvrage publié en 1781^{[réf. souhaitée]}, Laplace donne une première table de cette loi. En 1809, Carl Friedrich Gauss assimile des erreurs d'observation en astronomie à la courbe, dite des erreurs, de la densité d'une loi normale^{[a 2]}.

Une loi normale est alors pleinement définie lorsque le premier théorème central limite, alors appelé théorème de Laplace, est énoncé par Laplace en 1812^{[a 1]}. Son nom « normale » est donné par Henri Poincaré à la fin du XIX^e siècle^[10]. Les lois normales portent également les noms de lois de Gauss ou lois de Laplace-Gauss^[11] en fonction de l'attribution de la paternité de la création de ces lois ; la dénomination de deuxième loi de Laplace est également utilisée occasionnellement^[12].

Les études sur les lois normales se poursuivent durant le XIX^e siècle. Ainsi, de nouvelles tables numériques sont données en 1948 par Egon Sharpe Pearson, en 1952 par le National Bureau of Standards^[13] et en 1958 par Greenwood et Hartley^[14].

Loi normale centrée réduite[modifier | modifier le code]

Une loi normale est une loi de probabilité (c'est-à-dire une mesure N de masse totale unitaire^{[a 3]}) unidimensionnelle (c'est-à-dire à support réel ${\displaystyle \mathbb {R} }$). C'est une loi absolument continue, c'est-à-dire que la mesure est absolument continue par rapport à la mesure de Lebesgue. Autrement dit, il existe une densité de probabilité, souvent notée φ pour la loi normale centrée réduite, telle que : N(dx) = φ(x) dx. Elle est généralisée par la loi normale multidimensionnelle. La loi normale centrée réduite est appelée loi normale standard^[15].

Définition par la fonction de densité[modifier | modifier le code]

La loi normale centrée réduite est la loi de probabilité absolument continue dont la densité de probabilité est donnée par la fonction ${\displaystyle \varphi :\mathbb {R} \to \mathbb {R} _{+}}$ définie par^[16] : ${\displaystyle \varphi (t)={\frac {1}{\sqrt {2\pi }}}\operatorname {e} ^{-{\frac {1}{2}}t^{2}}}$, pour tout ${\displaystyle t\in \mathbb {R} }$. Cette loi est dite centrée puisque son moment d'ordre 1 (espérance) vaut 0 et réduite puisque son moment d'ordre 2 (variance) vaut 1, tout comme son écart type. Le graphe de la densité φ est appelé fonction gaussienne, courbe de Gauss ou courbe en cloche. Cette loi est notée grâce à la première lettre de « normal », une variable aléatoire X qui suit la loi normale centrée réduite est notée : ${\displaystyle X\sim {\mathcal {N}}(0,1)}$.

Quelques remarques et propriétés immédiates (voir également les propriétés ci-dessous) :

• le calcul de l'intégrale de Gauss permet de démontrer que la fonction φ est une densité de probabilité par la formule : ${\displaystyle \int _{-\infty }^{+\infty }\mathrm {exp} \left(-{\frac {t^{2}}{2}}\right)\,\mathrm {d} t={\sqrt {2\pi }}}$ ;
• la densité φ est continue, uniformément bornée et paire^[17] ;
• cette parité fait que l'espérance et les moments d'ordres impairs sont nuls ;
• les moments d'ordres pairs sont donnés par ${\displaystyle m_{2k}=(2k-1)\cdots 3\cdot 1={\frac {(2k)!}{2^{k}k!}}}$^[18](en particulier, Var(X) = m₂ = 1), d'après la relation de récurrence m_2k = (2k–1)m_2k–2 pour k ≥ 1, qui provient de l'intégration par parties suivante :${\displaystyle m_{2k}=\int _{-\infty }^{+\infty }t^{2k-1}t\varphi (t)\,\mathrm {d} t=-\int _{-\infty }^{+\infty }t^{2k-1}\varphi '(t)\,\mathrm {d} t=(2k-1)\int _{-\infty }^{+\infty }t^{2k-2}\varphi (t)\,\mathrm {d} t}$.
• le maximum de la fonction φ est atteint en la moyenne 0 et vaut^[17] ${\displaystyle {\frac {1}{\sqrt {2\pi }}}}$ ;
• la fonction vérifie : ${\displaystyle \lim _{x\to +\infty }\varphi (x)=\lim _{x\to -\infty }\varphi (x)=0}$ ;
• la densité φ est infiniment dérivable ; un raisonnement par récurrence permet d'obtenir la formule^[19] : ${\displaystyle \varphi ^{(n)}(x)=(-1)^{n}H_{n}(x)\varphi (x)}$ où H_n est le n-ième polynôme d'Hermite ;
• la densité possède^{[a 3]} deux points d'inflexion en 1 et en –1. Ce sont les points en lesquels la dérivée seconde φ'' s'annule et change de signe. Les deux points se situent approximativement aux trois cinquièmes de la hauteur totale.

Définition par la fonction de répartition[modifier | modifier le code]

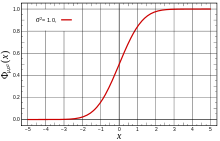
Historiquement, une loi normale est apparue comme la loi limite dans le théorème central limite à l'aide de sa fonction de répartition. Il est alors utile de définir la loi par cette fonction. La loi normale est la loi de probabilité dont la fonction de répartition est donnée par la fonction ${\displaystyle \Phi :\mathbb {R} \to \mathbb {R} _{+}}$ définie par^[18] : ${\displaystyle \Phi (x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}\operatorname {e} ^{-{\frac {1}{2}}t^{2}}\,\mathrm {d} t}$, pour tout ${\displaystyle x\in \mathbb {R} }$. Elle donne la probabilité qu'une variable aléatoire de loi normale appartienne à un intervalle ${\displaystyle [a,b]}$ : ${\displaystyle \mathbb {P} (X\in [a,b])=\Phi (b)-\Phi (a)}$ (pour plus de détails de calcul, voir la section Tables numériques et calculs).

Quelques remarques et propriétés immédiates :

• il n'existe pas d'expression analytique de la fonction de répartition Φ, c'est-à-dire qu'elle ne s'exprime pas à partir de fonctions usuelles mais devient elle-même une fonction usuelle^[20] ;
• elle s'exprime en fonction de la fonction d'erreur grâce aux deux formules équivalentes suivantes^{[a 4]} :
  1. ${\displaystyle \Phi (x)={\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)}$,
  2. ${\displaystyle \operatorname {erf} (x)=2\Phi \left(x{\sqrt {2}}\right)-1}$ ;
• elle est dérivable une infinité de fois et vérifie Φ'(x) = φ(x). L'écriture équivalente dΦ(x) = φ(x)dx permet de définir l'intégrale de Lebesgue-Stieltjes par rapport à la loi normale ;
• elle est absolument continue et strictement croissante, c'est donc une bijection^{[a 5]} de ${\displaystyle \mathbb {R} }$ dans ]0 ; 1[. Sa réciproque Φ⁻¹ existe et s'appelle la fonction probit. Cette fonction est utilisée pour le modèle probit^[21] ;
• par parité de la loi, Φ(–x) = 1 – Φ(x) et ainsi Φ(0) = 1/2. Ceci montre^{[a 5]} que la médiane de la loi normale centrée réduite est 0 ;
• par définition de la fonction de répartition, ${\displaystyle \Phi (x)=\mathbb {P} (X\leq x)}$ lorsque la variable aléatoire X suit la loi normale centrée réduite, ${\displaystyle X\sim {\mathcal {N}}(0,1)}$. Pour obtenir les valeurs de cette probabilité, il faut approcher cette fonction par d'autres fonctions usuelles et il existe des tables de valeurs (voir la section Table de la loi normale ci-dessous).

Définition par la fonction caractéristique[modifier | modifier le code]

La caractérisation d'une loi normale par sa fonction caractéristique présente un intérêt pour démontrer certaines propriétés, comme la stabilité par addition ou le théorème central limite. Cette fonction caractéristique ${\displaystyle \phi :\mathbb {R} \to \mathbb {R} _{+}}$, qui se calcule à partir de la densité de probabilité^[18],[22] et caractérise la loi, est donnée par : ${\displaystyle \phi (t)={\rm {e}}^{-{\frac {t^{2}}{2}}},\,\forall t\in \mathbb {R} }$. Cette fonction caractéristique est égale, à une constante multiplicative près, à la densité de probabilité de la loi : on dit que la fonction caractéristique d'une gaussienne est gaussienne^{[a 3]}.

Si une variable aléatoire X suit la loi normale centrée réduite de fonction caractéristique ϕ définie ci-dessus, alors^[23] la transformation linéaire Y = aX+b admet pour fonction caractéristique : ${\displaystyle \phi _{Y}(t)={\rm {e}}^{{\rm {i}}bt}\phi (at)}$. C'est donc une variable aléatoire de loi normale de moyenne b et de variance a².

Définition par la fonction génératrice des moments[modifier | modifier le code]

Une autre manière de définir une loi normale est par l'utilisation de sa fonction génératrice des moments ${\displaystyle M:\mathbb {R} \to \mathbb {R} _{+},\;t\mapsto \sum _{n=0}^{\infty }m_{n}{\frac {t^{n}}{n!}}=\mathbb {E} \left(\operatorname {e} ^{tX}\right)}$. Cette fonction, qui se calcule à partir de la fonction de densité^{[b 1]} et caractérise la loi, est donnée par^[24] : ${\displaystyle M(t)={\rm {e}}^{\frac {t^{2}}{2}}}$, pour tout ${\displaystyle t\in \mathbb {R} }$. On retrouve ainsi les valeurs des moments m_n (voir supra).

Loi normale générale[modifier | modifier le code]

Définition[modifier | modifier le code]

Plus généralement que la loi normale centrée réduite, une loi normale (non centrée et non réduite) est une loi de probabilité absolument continue dont l'un des quatre points suivants est vérifié :

• la densité de probabilité ${\displaystyle \varphi :\mathbb {R} \to \mathbb {R} _{+}}$ est donnée par^[16] :${\displaystyle \varphi (t)={\frac {1}{\sigma {\sqrt {2\pi }}}}\operatorname {e} ^{-{\frac {1}{2}}{\frac {(t-\mu )^{2}}{\sigma ^{2}}}}}$, pour tout ${\displaystyle t\in \mathbb {R} }$ ;
• la fonction de répartition ${\displaystyle F:\mathbb {R} \to \mathbb {R} _{+}}$ est donnée par :${\displaystyle F(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{x}\mathrm {e} ^{-{\frac {1}{2}}{\frac {(t-\mu )^{2}}{\sigma ^{2}}}}\,\mathrm {d} t}$, pour tout ${\displaystyle x\in \mathbb {R} }$ ;
• la fonction caractéristique ${\displaystyle \phi :\mathbb {R} \to \mathbb {C} }$ est donnée par^[25] :${\displaystyle \phi (t)={\rm {e}}^{\mu {\rm {i}}t-{\frac {1}{2}}\sigma ^{2}t^{2}}}$, pour tout ${\displaystyle t\in \mathbb {R} }$ ;
• la fonction génératrice des moments ${\displaystyle M:\mathbb {R} \to \mathbb {R} _{+}}$ est donnée par^{[26],[27],[b 2]} :${\displaystyle M(t)={\rm {e}}^{\mu t+{\frac {1}{2}}\sigma ^{2}t^{2}}}$, pour tout ${\displaystyle t\in \mathbb {R} }$,où ${\displaystyle \mu \in \mathbb {R} }$ et ${\displaystyle \sigma \in \mathbb {R} _{+}^{\star }}$.

Pour le cas où σ = 0, c'est une forme dégénérée de la loi normale, parfois appelée loi normale impropre^[25]. C'est alors la mesure de Dirac au point μ qui n'est pas absolument continue.

La valeur μ est la moyenne de la loi et σ est l'écart type alors que σ² en est la variance. Cette loi est notée grâce à la première lettre de « normal ». Une variable aléatoire X qui suit une loi normale est notée de deux manières différentes suivant les auteurs^[28],[15] :${\displaystyle X\sim {\mathcal {N}}(\mu ,\sigma ){\text{ ou }}X\sim {\mathcal {N}}(\mu ,\sigma ^{2}).}$ La deuxième notation a l'intérêt de pouvoir noter la stabilité par addition de manière simple^{[a 5]} ; elle sera utilisée dans cet article.

Remarques et propriétés immédiates[modifier | modifier le code]

• Si la variable aléatoire X suit la loi normale centrée réduite ${\displaystyle {\mathcal {N}}(0,1)}$, alors la variable aléatoire σX + μ suit la loi normale ${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$ de moyenne μ et de variance σ². Réciproquement, si Y suit la loi normale ${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$, alors Y – μ/σ suit la loi normale centrée réduite^[1]. Dit autrement, toute loi normale peut s'obtenir par translation (shifting en anglais) et par dilatation (scaling en anglais) de la loi centrée réduite.Cette première propriété permet d'obtenir la formule très utile^[29] :${\displaystyle \mathbb {P} (Y\leq x)=\mathbb {P} \left({\frac {Y-\mu }{\sigma }}\leq {\frac {x-\mu }{\sigma }}\right)=\mathbb {P} \left(X\leq {\frac {x-\mu }{\sigma }}\right)}$.Il est alors possible de déduire les propriétés d'une loi normale à partir de celles de la loi normale centrée réduite, et vice versa. La variable Y – μ/σ est parfois^[30] appelée la « standardisation » de Y ou « variable Y centrée réduite ».
• Plus généralement, si ${\displaystyle X\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$ alors ${\displaystyle aX+b\sim {\mathcal {N}}(a\mu +b,a^{2}\sigma ^{2})}$ (on peut le lire sur les fonctions génératrices des moments^[31], ou sur les densités).
• La densité f est symétrique par rapport à μ^[17].
• Le maximum de la fonction f est atteint en μ et vaut^[17] ${\displaystyle {\frac {1}{\sigma {\sqrt {2\pi }}}}}$.
• La décroissance de la densité à droite et à gauche de μ est surexponentielle^[17].
• Puisqu'une loi normale est une loi de probabilité absolument continue, l'événement [X = x] est négligeable, c'est-à-dire que presque sûrement une variable aléatoire de loi normale X n'est jamais égale à une valeur fixée x. Ceci se traduit mathématiquement par : ${\displaystyle \mathbb {P} (X=x)=0}$.
• La largeur à mi-hauteur permet de donner une valeur d'amplitude de la loi. C'est la largeur de la courbe à une hauteur qui vaut la moitié de la hauteur totale. Cette largeur à mi-hauteur de la loi normale est proportionnelle à l'écart type^{[a 6]} : H = 2 √2 ln (2) σ ≈ 2,3548 σ. Le facteur 2 est issu de la propriété de symétrie de la loi normale.
• La densité possède^{[a 3]} deux points d'inflexion en μ + σ et en μ – σ. Ce sont les points en lesquels la dérivée seconde f'' s'annule et change de signe. Les deux points se situent approximativement aux trois cinquièmes de la hauteur totale.
• Les lois normales sont des lois de la famille exponentielle, c'est-à-dire que leur densité s'écrit sous la forme :${\displaystyle f(x)=a(\theta )b(x)\mathrm {e} ^{-c(\theta )d(x)}}$ ou, de manière équivalente, sous la forme^[32]${\displaystyle f(x)=\exp \left({\frac {x\theta _{1}-\beta (\theta _{1})}{\alpha (\theta _{2})}}\right),\ {\textrm {avec}}\ \theta _{1}=\mu ,\,\theta _{2}=\sigma ,\,\beta (\mu )=\mu ^{2}/2\ {\textrm {et}}\ \alpha (\sigma )=\sigma ^{2}}$.

Propriétés[modifier | modifier le code]

Autres caractérisations[modifier | modifier le code]

En addition de la densité de probabilité, de la fonction de répartition, de la fonction caractéristique et de la fonction génératrice des moments, il existe d'autres caractérisations des lois normales.

• Caractérisation due à Georges Darmois (1951) et Sergueï Bernstein (1954)^{[a 2]} : si deux variables aléatoires X₁ et X₂ sont indépendantes et de même loi et si les deux variables aléatoires X₁ + X₂ et X₁ – X₂ sont également indépendantes, alors la loi commune X₁ et X₂ est une loi normale.
• Caractérisation due à Charles Stein (1972)^{[a 3]} : les lois normales sont les seules lois de probabilité (mesures de probabilité) ${\displaystyle \mathbb {P} }$ telles que, pour toute fonction g de classe C¹ (c'est-à-dire dérivable et de dérivée continue) :${\displaystyle \int _{\mathbb {R} }g'(x)\mathrm {d} \mathbb {P} (x)=\int _{\mathbb {R} }xg(x)\mathrm {d} \mathbb {P} (x)}$.

Moments[modifier | modifier le code]

Le moment d'ordre 1 est appelé la moyenne (μ) et est donné en paramètre d'une loi normale ${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$. Le deuxième paramètre est son écart type (σ), c'est-à-dire la racine carrée de la variance qui est par définition la moyenne des carrés des écarts à la moyenne. Il est alors également intéressant d'obtenir les moments centrés d'une loi normale, ils sont donnés par^[31] :

${\displaystyle {\begin{cases}\mu _{2k}=\mathbb {E} [(X-\mu )^{2k}]={\frac {(2\,k)!}{2^{k}k!}}\sigma ^{2k}\\\mu _{2k+1}=\mathbb {E} [(X-\mu )^{2k+1}]=0\end{cases}}}$ pour ${\displaystyle k\geq 0}$ et X une variable aléatoire de loi normale ${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$.

Le moment ordinaire m_n peut s'obtenir à partir des moments d'ordre inférieur à n – 1 et du moment centré d'ordre n, en utilisant la formule qui exprime μ_n en fonction de m₀, m₁, ..., m_n. Les premiers moments d'une loi normale sont alors^[33] : ${\displaystyle m_{1}=\mathbb {E} [X]=\mu ,\quad m_{2}=\mathbb {E} [X^{2}]=\sigma ^{2}+\mu ^{2},\quad m_{3}=\mathbb {E} [X^{3}]=3\mu \sigma ^{2}+\mu ^{3},\quad m_{4}=\mathbb {E} [X^{4}]=3\sigma ^{4}+6\sigma ^{2}\mu ^{2}+\mu ^{4}}$.

Calcul direct[modifier | modifier le code]

Grâce à la symétrie autour de μ de la fonction de densité d'une loi normale, les moments centrés d'ordre impair sont tous nuls^[31].

Des moments d'ordre pairs de la loi normale centrée réduite (voir supra), on déduit la formule des moments centrés : ${\displaystyle \mu _{2k}={\frac {(2\,k)!}{2^{k}k!}}\sigma ^{2k}}$.

Par la fonction génératrice des moments[modifier | modifier le code]

Les moments centrés (μ_n, n ≥ 0) d'une loi peuvent s'obtenir à partir de la fonction génératrice des moments centrés. Le cas particulier μ = 0 de la fonction génératrice des moments (voir supra) donne : ${\displaystyle M_{\text{centré}}(t)={\rm {e}}^{\frac {\sigma ^{2}t^{2}}{2}}=\sum _{k=0}^{\infty }{\frac {1}{k!}}\left({\frac {\sigma ^{2}t^{2}}{2}}\right)^{k}}$.

Comme par ailleurs on a (pour toute loi) ${\displaystyle M_{\text{centré}}(t)=\sum _{n=0}^{\infty }{\frac {1}{n!}}\mu _{n}t^{n}}$, on en déduit, par identification des coefficients des deux séries^[31], les moments centrés d'une loi normale (voir supra).

Quant aux moments ordinaires, leur fonction génératrice permet d'établir la relation de récurrence^{[b 3]} :

${\displaystyle m_{n+1}=\mu m_{n}+n\sigma ^{2}m_{n-1}\quad (n\geq 1)}$.

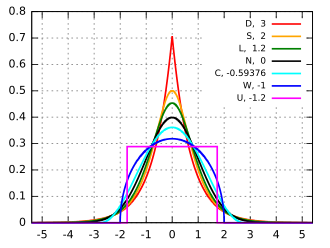
Asymétrie et aplatissement[modifier | modifier le code]

L'asymétrie γ₁, le kurtosis β₂ et le kurtosis normalisé γ₂ s'obtiennent à partir des formules des moments^[34] :

${\displaystyle \gamma _{1}={\frac {\mu _{3}}{\sigma ^{3}}}=0}$ ;
${\displaystyle \beta _{2}={\frac {\mu _{4}}{\sigma ^{4}}}=3}$ ;
${\displaystyle \gamma _{2}=\beta _{2}-3=0}$.

Les lois normales servent de point de référence pour la comparaison des épaisseurs de traîne : si une loi possède un kurtosis normalisé γ₂ > 0, alors la loi possède une traîne plus épaisse qu'une loi normale et est dite leptokurtique ; à l'inverse si γ₂ < 0, la loi possède une traîne moins épaisse qu'une loi normale et est appelée platikurtique ; les lois de kurtosis normalisé nul possèdent une traîne comparable à la loi normale et sont dites mésokurtiques.

Cumulants[modifier | modifier le code]

La fonction caractéristique permet d'obtenir la fonction génératrice des cumulants par la formule ${\displaystyle \ln(\phi (t))=\sum _{n=1}^{+\infty }K_{n}{\frac {({\rm {i}}t)^{n}}{n!}}}$ et permet d'obtenir les cumulants^[35] : K₁ = μ, K₂ = σ² et K_n = 0 pour n ≥ 3.

Théorèmes de convergence[modifier | modifier le code]

La première version du théorème central limite, appelé alors théorème de Moivre-Laplace, a été énoncée dans le cas de variables aléatoires de loi de Bernoulli. De manière plus générale, si X₁, X₂, ..., X_n sont des variables indépendantes et identiquement distribuées de variance finie et si la somme est notée S_n = X₁ + X₂ + ... + X_n, alors^[20] pour tout a < b ${\displaystyle \lim _{n\to +\infty }\mathbb {P} \left(a\leq {\frac {S_{n}-\mathbb {E} [S_{n}]}{\sqrt {\operatorname {Var} (S_{n})}}}\leq b\right)=\int _{a}^{b}\varphi (x)\,\mathrm {d} x}$ où φ est la densité de probabilité de la loi normale centrée réduite.

Ce théorème signifie que tout ce qui peut être considéré comme étant la somme d'une grande quantité de petites valeurs aléatoires indépendantes et identiquement distribuées est approximativement de loi normale^[36]. Ceci montre le caractère central des lois normales en théorie des probabilités. Un énoncé physique de ce théorème peut être formulé^[37] : Si une grandeur physique subit l'influence additive d'un nombre important de facteurs indépendants et si l'influence de chaque facteur pris séparément est petite, alors la distribution de cette grandeur est une distribution gaussienne.

Ce théorème central limite est valide pour toute loi de probabilité initiale des variables iid X₁, X₂, ..., X_n ayant un écart type fini, il permet d'obtenir de bonnes approximations de la somme S_n, par exemple^[38] :

• si les variables X_i sont de loi de Bernoulli ${\displaystyle {\mathcal {B}}(p)}$, alors S_n suit approximativement une loi normale ${\displaystyle {\mathcal {N}}(np,np(1-p))}$. Cette approximation est satisfaisante^[39] dans le cas où np(1–p) > 10 ;
• si les variables X_i sont de loi du χ² : χ²(1), alors S_n suit approximativement une loi normale ${\displaystyle {\mathcal {N}}(n,4n^{2})}$ ;
• si les variables X_i sont de loi exponentielle : ${\displaystyle {\mathcal {E}}(\lambda )}$, alors S_n suit approximativement une loi normale ${\displaystyle {\mathcal {N}}\left({\frac {n}{\lambda }},{\frac {n}{\lambda ^{2}}}\right)}$.

Il existe des versions plus générales de ce théorème, par exemple en considérant des variables aléatoires indépendantes, pas de même loi mais ayant des variances petites comparées à celle de leur moyenne^[40]. Un théorème de Gnedenko et Kolmogorov (1954) stipule qu'une variable aléatoire normale est la somme d'un grand nombre de variables aléatoires indépendantes petites dont aucune n'est prépondérante :

Stabilités et famille normale[modifier | modifier le code]

Stabilité par additivité (propriété de conservation)[modifier | modifier le code]

Les lois normales sont stables par additivité^{[a 2]}, c'est-à-dire que la somme de deux variables aléatoires indépendantes de lois normales est elle-même une variable aléatoire de loi normale. Plus explicitement : si ${\displaystyle X_{1}\sim {\mathcal {N}}(\mu _{1},\sigma _{1}^{2})}$, ${\displaystyle X_{2}\sim {\mathcal {N}}(\mu _{2},\sigma _{2}^{2})}$ et X₁ et X₂ sont indépendantes, alors la variable aléatoire ${\displaystyle X_{1}+X_{2}}$ suit la loi normale ${\displaystyle {\mathcal {N}}(\mu _{1}+\mu _{2},\sigma _{1}^{2}+\sigma _{2}^{2})}$.

Cette propriété se généralise pour n variables, c'est-à-dire si pour tout ${\displaystyle i\in \{1,2,\dots ,n\}}$, les variables aléatoires X_i suivent une loi normale ${\displaystyle {\mathcal {N}}(\mu _{i},\sigma _{i}^{2})}$ et sont indépendantes, alors^[41] la somme X₁ + X₂ + ... + X_n suit une loi normale ${\displaystyle {\mathcal {N}}(\mu _{1}+\mu _{2}+\dots +\mu _{n},\sigma _{1}^{2}+\sigma _{2}^{2}+\dots +\sigma _{n}^{2})}$.

Cette propriété se démontre directement au moyen des fonctions caractéristiques. La densité de probabilité de la somme de deux variables indépendantes de loi normale est donnée par la convolution des deux densités. Ceci se traduit par les formules de convolution de fonctions^[25] ou de convolution de mesures normales^[42] que l'on note ${\displaystyle {\mathcal {N}}_{\mu _{1},\sigma _{1}^{2}}}$ : ${\displaystyle \varphi \left({\frac {x-\mu _{1}}{\sigma _{1}}}\right)\ast \varphi \left({\frac {x-\mu _{2}}{\sigma _{2}}}\right)=\varphi \left({\frac {x-(\mu _{1}+\mu _{2})}{\sqrt {\sigma _{1}^{2}+\sigma _{2}^{2}}}}\right)}$ et ${\displaystyle {\mathcal {N}}_{\mu _{1},\sigma _{1}^{2}}\ast {\mathcal {N}}_{\mu _{2},\sigma _{2}^{2}}={\mathcal {N}}_{\mu _{1}+\mu _{2},\sigma _{1}^{2}+\sigma _{2}^{2}}}$.

Il ne faut pas confondre avec la loi dont la densité est la somme de densités de lois normales (voir la section Constructions à partir de la loi normale ci-dessous).

Famille normale[modifier | modifier le code]

L'ensemble de fonctions ${\displaystyle \{\varphi ({\frac {x-\mu }{\sigma }})\mid \mu \in \mathbb {R} ,\sigma >0\}}$ forme la famille dite famille normale. La famille normale est également le nom de l'ensemble des lois normales^[42] ${\displaystyle \{{\mathcal {N}}_{\mu ,\sigma ^{2}}\mid \mu \in \mathbb {R} ,\sigma >0\}}$. La famille de fonctions est fermée pour la convolution au sens où^[43] : la fonction φ est la seule qui engendre la famille ; si la convolution de deux densités est dans la famille alors les deux fonctions sont dans la famille ; et toute densité convolée un nombre suffisamment grand de fois et convenablement renormalisée est proche d'une fonction de la famille normale. Les trois théorèmes suivants donnent plus de précisions mathématiques.

1. Théorème^[43] : si pour une fonction de densité f de moyenne 0 et d'écart type 1, il existe ${\displaystyle \mu \in \mathbb {R} }$ et ${\displaystyle \sigma \in \mathbb {R} _{+}^{*}}$ satisfaisant :${\displaystyle f\left({\frac {x-\mu _{1}}{\sigma _{1}}}\right)\ast f\left({\frac {x-\mu _{2}}{\sigma _{2}}}\right)=f\left({\frac {x-\mu }{\sigma }}\right)}$,alors ${\displaystyle f\equiv \varphi }$ est la densité de la loi normale centrée réduite.
2. Théorème de Lévy-Cramér (1936) (conjecturé par Paul Lévy en 1935)^{[44],[a 2]} : si deux fonctions de densité, f₁ et f₂, vérifient :${\displaystyle f_{1}(x)\ast f_{2}(x)=\varphi \left({\frac {x-\mu }{\sigma }}\right)}$,alors${\displaystyle f_{1}(x)=\varphi \left({\frac {x-\mu _{1}}{\sigma _{1}}}\right)}$ et ${\displaystyle f_{2}(x)=\varphi \left({\frac {x-\mu _{2}}{\sigma _{2}}}\right)}$ avec μ₁ + μ₂ = μ et σ₁ + σ₂ = σ. Autrement dit, si la somme de deux variables aléatoires indépendantes est normale, alors les deux variables sont de lois normales.
3. Théorème^[44] : si f est la densité commune de n variables aléatoires indépendantes de moyenne 0 et d'écart type 1, alors la convolée n fois de f converge uniformément en x : ${\displaystyle \left(f(x/{\sqrt {n}})\right)^{\ast n}\to \varphi (x)}$ (ce théorème est équivalent au théorème central limite). Il ne faut pas confondre cette famille normale avec la famille normale de fonctions holomorphes.

Stabilité par linéarité[modifier | modifier le code]

Les lois normales sont stables par linéarité : si α ≥ 0 et β sont deux réels et ${\displaystyle X\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$, alors^[45] la variable aléatoire αX + β suit la loi normale ${\displaystyle {\mathcal {N}}(\alpha \mu +\beta ,\alpha ^{2}\sigma ^{2})}$.

Grâce aux stabilités par addition et par linéarité, une loi normale est un cas particulier de loi stable^{[a 7]} avec pour paramètre de stabilité α = 2. Parmi les lois stables, les lois normales, la loi de Lévy (α = 1/2) et la loi de Cauchy (α = 1) sont les seules à posséder une expression analytique de leur fonction de densité.

Stabilité par moyenne[modifier | modifier le code]

Les lois normales sont stables par moyennisation, c'est-à-dire si X₁, X₂, ..., X_n sont des variables aléatoires indépendantes suivant respectivement les lois normales ${\displaystyle {\mathcal {N}}(\mu _{1},\sigma _{1}^{2}),{\mathcal {N}}(\mu _{2},\sigma _{2}^{2}),\dots ,{\mathcal {N}}(\mu _{n},\sigma _{n}^{2})}$, alors la moyenne 1/n(X₁ + X₂ + ... + X_n) suit la loi ${\displaystyle {\mathcal {N}}\left({\tfrac {\mu _{1}+\mu _{2}+\dots +\mu _{n}}{n}},{\tfrac {\sigma _{1}^{2}+\sigma _{2}^{2}+\dots +\sigma _{n}^{2}}{n^{2}}}\right)}$.

Convexité[modifier | modifier le code]

Les lois normales ne sont pas convexe^[46], c'est-à-dire que l'inégalité ${\displaystyle \lambda \mathbb {P} (A)+(1-\lambda )\mathbb {P} (B)\leq \mathbb {P} (\lambda A+(1-\lambda )B)}$ pour tous boréliens A et B n'est pas vérifiée lorsque la mesure ${\displaystyle \mathbb {P} }$ est normale. Cependant, lorsque l'on normalise cette inégalité avec l'inverse de la fonction de répartition de la loi normale centrée réduite, on obtient le théorème suivant, analogue à l'inégalité de Brunn-Minkowski-Lusternik pour la mesure de Lebesgue dans ${\displaystyle \mathbb {R} ^{n}}$ :

Inégalité de Ehrhard — Pour la mesure normale standard ${\displaystyle {\mathcal {N}}_{0,1}}$, pour tous ensembles boréliens A et B et pour tout λ ∈ ]0 ; 1[,

${\displaystyle \lambda \Phi ^{-1}\left({\mathcal {N}}_{0,1}(A)\right)+(1-\lambda )\Phi ^{-1}\left({\mathcal {N}}_{0,1}(B)\right)\leq \Phi ^{-1}\left({\mathcal {N}}_{0,1}(\lambda A+(1-\lambda )B)\right)}$.

En fait, les lois normales font partie de la famille des distributions de mesures log-concaves, c'est-à-dire vérifiant pour tous boréliens A et B et tout ${\displaystyle \lambda \in ]0,1[}$,

${\displaystyle \mathbb {P} (\lambda A+(1-\lambda )B)\geq \mathbb {P} (A)^{\lambda }\mathbb {P} (B)^{1-\lambda }.}$

Entropie et quantité d'information[modifier | modifier le code]

Entropie de Shannon[modifier | modifier le code]

L'entropie de Shannon d'une loi de probabilité absolument continue de densité donnée par f permet de mesurer une quantité d'information et est définie par : ${\displaystyle H=-\int _{-\infty }^{+\infty }f(x)\ln f(x)\,\mathrm {d} x}$. Dans l'ensemble des lois absolument continues de variance σ² fixée, les lois normales ${\displaystyle {\mathcal {N}}(\cdot ,\sigma ^{2})}$ sont d'entropie maximum^{[a 8]}. L'entropie maximum, pour une loi normale donc, est donnée par : H = ln (σ √2πe). Ainsi la théorie de maximisation de l'entropie dit que, même si elle n'est pas la meilleure loi adaptée aux valeurs, une loi normale ajustée aux valeurs est adéquate pour prendre une décision.

Il y a également une connexion entre la convergence de suites de lois de probabilité vers une loi normale et la croissance de l'entropie, ce qui en fait un outil majeur dans la théorie de l'information^{[a 2]}.

La quantité d'information de Fisher[modifier | modifier le code]

L'information de Fisher d'une loi à densité de probabilité est une autre notion de quantité d'information. Pour une densité f, elle est donnée par : ${\displaystyle I=\int _{-\infty }^{+\infty }\left({\frac {f'(x)}{f(x)}}\right)^{2}f(x)\,\mathrm {d} x}$. Pour toute densité suffisamment régulière d'une loi centrée réduite, cette information vérifie I ≥ 1. Les lois normales se distinguent des autres densités puisque l'inégalité précédente est une égalité si et seulement si la densité est celle de la loi normale centrée réduite^{[a 2]}.

Distance entre lois[modifier | modifier le code]

La divergence de Kullback-Leibler entre deux lois permet de mesurer une distance entre les deux lois, ou une perte d'information entre les deux lois. La divergence de Kullback-Leibler entre les deux lois normales ${\displaystyle {\mathcal {N}}(\mu _{1},\sigma _{1}^{2})}$ et ${\displaystyle {\mathcal {N}}(\mu _{2},\sigma _{2}^{2})}$ est : ${\displaystyle D_{KL}({\mathcal {N}}(\mu _{1},\sigma _{1}^{2})\|{\mathcal {N}}(\mu _{2},\sigma _{2}^{2}))=\log \left({\frac {\sigma _{2}}{\sigma _{1}}}\right)+{\frac {1}{2}}\left({\frac {\sigma _{1}^{2}}{\sigma _{2}^{2}}}+{\frac {(\mu _{2}-\mu _{1})^{2}}{\sigma _{2}^{2}}}-1\right)}$. Cette divergence est nulle pour μ₁ = μ₂ et σ₁ = σ₂ ; de plus, elle croît lorsque ${\displaystyle |\mu _{1}-\mu _{2}|}$ croît^{[a 9]}.

Approximation de la fonction de répartition[modifier | modifier le code]

Il n'existe pas d'expression analytique pour la fonction de répartition Φ de la loi normale centrée réduite, c'est-à-dire qu'il n'existe pas de formule simple entre la fonction de répartition et les fonctions classiques telles que les fonctions polynomiales, exponentielle, logarithmique, trigonométriques, etc. Cependant la fonction de répartition apparaît dans plusieurs résultats à vocation à être appliqués, il est donc important de mieux cerner cette fonction. Différentes écritures sous forme de séries ou de fractions continues généralisées sont possibles^[47].

Pour les valeurs de ${\displaystyle 0<x\ll 1}$, la fonction de répartition de la loi normale centrée réduite s'écrit sous la forme^{[a 10]} : ${\displaystyle \Phi (x)={\frac {1}{2}}+{\frac {1}{\sqrt {2\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{n!2^{n}(2n+1)}}x^{2n+1}={\frac {1}{2}}+{\frac {1}{\sqrt {2\pi }}}\left(x-{\frac {x^{3}}{6}}+{\frac {x^{5}}{40}}+\dots \right)}$, ou sous la forme : ${\displaystyle \Phi (x)={\frac {1}{2}}+\varphi (x)\sum _{n=0}^{\infty }{\frac {1}{1\cdot 3\cdot 5\dots (2n+1)}}x^{2n+1}={\frac {1}{2}}+\varphi (x)\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{15}}+\dots \right)}$.

Pour ${\displaystyle 1\ll x}$, la fonction de répartition de la loi normale centrée réduite s'écrit sous la forme^{[47],[a 10]} : ${\displaystyle \Phi (x)=1-{\frac {\varphi (x)}{x}}\left(1-{\frac {1}{x^{2}}}+{\frac {1\cdot 3}{x^{4}}}-{\frac {1\cdot 3\cdot 5}{x^{6}}}+\dots +{\frac {1\cdot 3\dots (2n-1)}{x^{2n}}}\right)+R_{n}}$ avec ${\displaystyle R_{n}=(-1)^{n+1}1\cdot 3\dots (2n+1)\int _{x}^{\infty }{\frac {\varphi (y)}{y^{2n+2}}}\,\mathrm {d} y}$.

De manière plus numérique et facilement calculable, les approximations suivantes donnent des valeurs de la fonction de répartition Φ de la loi normale centrée réduite avec :

• une erreur de l'ordre de^[48] 10⁻⁵ : pour x > 0, ${\displaystyle \Phi (x)=1-{\frac {{\rm {e}}^{-{\frac {x^{2}}{2}}}}{\sqrt {2\pi }}}\left({\frac {0{,}4361836}{1+0{,}33267\,x}}+{\frac {-0{,}1201676}{(1+0{,}33267\,x)^{2}}}+{\frac {0{,}9372980}{(1+0{,}33267\,x)^{3}}}\right)+\epsilon (x)}$ où ${\displaystyle |\epsilon (x)|<10^{-5}}$ ;
• une erreur de l'ordre de^[48] ${\displaystyle 2{,}5\,.\,10^{-4}}$ : pour ${\displaystyle x>0}$ : ${\displaystyle \Phi (x)\approx 1-{\frac {1}{2\left(1+0{,}196854\,x+0{,}115194\,x^{2}+0{,}000344\,x^{3}+0{,}019527\,x^{4}\right)^{4}}}}$ ;
• une erreur de l'ordre de^{[a 10]} ${\displaystyle 10^{-2}}$ : ${\displaystyle \Phi (x)={\begin{cases}0{,}1x(4{,}4-x)+0,5&{\text{ pour }}0\leq x\leq 2{,}2\\0{,}99&{\text{ pour }}2{,}2\leq x\leq 2{,}6\\1&{\text{ pour }}x\geq 2{,}6.\end{cases}}}$

Voici un exemple d'algorithme^{[a 4]} pour le langage C :

double Phi(double x){    long double s=x,t=0,b=x,q=x*x,i=1;     while(s!=t)       s = (t=s) + (b*=q/(i+=2));    return 0.5 + s*exp(-0.5*q - 0.91893853320467274178L); } 

Une autre écriture de la fonction de répartition de la loi normale centrée réduite utilise une fraction continue généralisée^{[a 4]} : ${\displaystyle \Phi (x{\sqrt {2}})={\frac {1}{2}}-{\cfrac {1}{\sqrt {\pi }}}{\cfrac {{\cfrac {1}{2}}{\rm {e}}^{-x^{2}}}{x+{\cfrac {1}{2x+{\cfrac {2}{x+{\cfrac {3}{2x+{\cfrac {4}{x+\dots }}}}}}}}}}}$.

Tables numériques et calculs[modifier | modifier le code]

Comme mentionné dans la section précédente, il est utile de bien connaître la fonction de répartition Φ pour les applications numériques. Des tables de valeurs ont alors été calculées pour la fonction de répartition, mais également pour son inverse, ce qui permet d'obtenir les quantiles et les intervalles de confiance pour un seuil de tolérance fixé.^{[réf. nécessaire]}

Table de valeurs de la fonction de répartition

La table suivante donne les valeurs de la fonction de répartition ${\displaystyle \Phi (x)=\mathbb {P} [X\leq x]}$, lorsque X suit la loi normale centrée réduite ${\displaystyle {\mathcal {N}}(0,1)}$.

Les valeurs en début de lignes donnent la première partie de la variable, les valeurs en début de colonnes donnent la deuxième partie. Ainsi la case de la deuxième ligne et troisième colonne donne : Φ(0,12) = 0,54776.

Table de valeur de la fonction de répartition de la loi normale

${\displaystyle \Phi (x)}$	0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,0	0,50000	0,50399	0,50798	0,51197	0,51595	0,51994	0,52392	0,52790	0,53188	0,53586
0,1	0,53983	0,54380	0,54776	0,55172	0,55567	0,55962	0,56356	0,56749	0,57142	0,57535
0,2	0,57926	0,58317	0,58706	0,59095	0,59483	0,59871	0,60257	0,60642	0,61026	0,61409
0,3	0,61791	0,62172	0,62552	0,62930	0,63307	0,63683	0,64058	0,64431	0,64803	0,65173
0,4	0,65542	0,65910	0,66276	0,66640	0,67003	0,67364	0,67724	0,68082	0,68439	0,68793
0,5	0,69146	0,69497	0,69847	0,70194	0,70540	0,70884	0,71226	0,71566	0,71904	0,72240
0,6	0,72575	0,72907	0,73237	0,73565	0,73891	0,74215	0,74537	0,74857	0,75175	0,75490
0,7	0,75804	0,76115	0,76424	0,76730	0,77035	0,77337	0,77637	0,77935	0,78230	0,78524
0,8	0,78814	0,79103	0,79389	0,79673	0,79955	0,80234	0,80511	0,80785	0,81057	0,81327
0,9	0,81594	0,81859	0,82121	0,82381	0,82639	0,82894	0,83147	0,83398	0,83646	0,83891
1,0	0,84134	0,84375	0,84614	0,84849	0,85083	0,85314	0,85543	0,85769	0,85993	0,86214
1,1	0,86433	0,86650	0,86864	0,87076	0,87286	0,87493	0,87698	0,87900	0,88100	0,88298
1,2	0,88493	0,88686	0,88877	0,89065	0,89251	0,89435	0,89617	0,89796	0,89973	0,90147
1,3	0,90320	0,90490	0,90658	0,90824	0,90988	0,91149	0,91309	0,91466	0,91621	0,91774
1,4	0,91924	0,92073	0,92220	0,92364	0,92507	0,92647	0,92785	0,92922	0,93056	0,93189
1,5	0,93319	0,93448	0,93574	0,93699	0,93822	0,93943	0,94062	0,94179	0,94295	0,94408
1,6	0,94520	0,94630	0,94738	0,94845	0,94950	0,95053	0,95154	0,95254	0,95352	0,95449
1,7	0,95543	0,95637	0,95728	0,95818	0,95907	0,95994	0,96080	0,96164	0,96246	0,96327
1,8	0,96407	0,96485	0,96562	0,96638	0,96712	0,96784	0,96856	0,96926	0,96995	0,97062
1,9	0,97128	0,97193	0,97257	0,97320	0,97381	0,97441	0,97500	0,97558	0,97615	0,97670
2,0	0,97725	0,97778	0,97831	0,97882	0,97932	0,97982	0,98030	0,98077	0,98124	0,98169
2,1	0,98214	0,98257	0,98300	0,98341	0,98382	0,98422	0,98461	0,98500	0,98537	0,98574
2,2	0,98610	0,98645	0,98679	0,98713	0,98745	0,98778	0,98809	0,98840	0,98870	0,98899
2,3	0,98928	0,98956	0,98983	0,99010	0,99036	0,99061	0,99086	0,99111	0,99134	0,99158
2,4	0,99180	0,99202	0,99224	0,99245	0,99266	0,99286	0,99305	0,99324	0,99343	0,99361
2,5	0,99379	0,99396	0,99413	0,99430	0,99446	0,99461	0,99477	0,99492	0,99506	0,99520
2,6	0,99534	0,99547	0,99560	0,99573	0,99585	0,99598	0,99609	0,99621	0,99632	0,99643
2,7	0,99653	0,99664	0,99674	0,99683	0,99693	0,99702	0,99711	0,99720	0,99728	0,99736
2,8	0,99744	0,99752	0,99760	0,99767	0,99774	0,99781	0,99788	0,99795	0,99801	0,99807
2,9	0,99813	0,99819	0,99825	0,99831	0,99836	0,99841	0,99846	0,99851	0,99856	0,99861
3,0	0,99865	0,99869	0,99874	0,99878	0,99882	0,99886	0,99889	0,99893	0,99896	0,99900
3,1	0,99903	0,99906	0,99910	0,99913	0,99916	0,99918	0,99921	0,99924	0,99926	0,99929
3,2	0,99931	0,99934	0,99936	0,99938	0,99940	0,99942	0,99944	0,99946	0,99948	0,99950
3,3	0,99952	0,99953	0,99955	0,99957	0,99958	0,99960	0,99961	0,99962	0,99964	0,99965
3,4	0,99966	0,99968	0,99969	0,99970	0,99971	0,99972	0,99973	0,99974	0,99975	0,99976
3,5	0,99977	0,99978	0,99978	0,99979	0,99980	0,99981	0,99981	0,99982	0,99983	0,99983
3,6	0,99984	0,99985	0,99985	0,99986	0,99986	0,99987	0,99987	0,99988	0,99988	0,99989
3,7	0,99989	0,99990	0,99990	0,99990	0,99991	0,99992	0,99992	0,99992	0,99992	0,99992
3,8	0,99993	0,99993	0,99993	0,99994	0,99994	0,99994	0,99994	0,99995	0,99995	0,99995
3,9	0,99995	0,99995	0,99996	0,99996	0,99996	0,99996	0,99996	0,99996	0,99997	0,99997

 

Tables de valeurs des quantiles

Les deux tables suivantes donnent^[49] les valeurs du quantile ${\displaystyle q_{p}}$ de la loi normale centrée réduite ${\displaystyle {\mathcal {N}}(0,1)}$ défini par ${\displaystyle q_{p}=\Phi ^{-1}(p)}$.

Les valeurs en début de ligne donne la première partie de la variable, les valeurs en début de colonne donne la deuxième partie. Ainsi la case de la deuxième ligne et troisième colonne donne : ${\displaystyle q_{0{,}62}=\Phi ^{-1}(0{,}62)=0{,}3055}$.

Table de valeurs des quantiles ${\displaystyle q_{p}}$

${\displaystyle q_{p}}$	0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,50	0,0000	0,0251	0,0502	0,0753	0,1004	0,1257	0,1510	0,1764	0,2019	0,2275
0,60	0,2533	0,2793	0,3055	0,3319	0,3585	0,3853	0,4125	0,4399	0,4677	0,4959
0,70	0,5244	0,5534	0,5828	0,6128	0,6433	0,6745	0,7063	0,7388	0,7722	0,8064
0,80	0,8416	0,8779	0,9154	0,9542	0,9945	1,036	1,080	1,126	1,175	1,227
0,90	1,282	1,341	1,405	1,476	1,555	1,645	1,751	1,881	2,054	2,326

Cette table donne les valeurs des quantiles pour p grand.

Table de valeur des quantiles ${\displaystyle q_{p}}$

p	0,975	0,995	0,999	0,9995	0,9999	0,99995	0,99999	0,999995
${\displaystyle q_{p}}$	1,9600	2,5758	3,0902	3,2905	3,7190	3,8906	4,2649	4,4172

 

Les tables sont données pour les valeurs positives de la loi normale centrée réduite. Grâce aux formules de la fonction de répartition, il est possible d'obtenir d'autres valeurs.

Les valeurs négatives de la fonction de répartition sont données par la formule^[14] Φ(–x) = 1 – Φ(x). Par exemple : ${\displaystyle \Phi (-1{,}07)=\mathbb {P} [X\leq -1{,}07]\approx 1-0{,}85769=0{,}14231}$ pour ${\displaystyle X\sim {\mathcal {N}}(0,1)}$.

Les valeurs de la fonction de répartition de la loi générale s'obtiennent par la formule^[50] ${\displaystyle F(y)=\Phi ({\frac {y-\mu }{\sigma }})}$. Par exemple^[51] : ${\displaystyle F(12{,}14)=\mathbb {P} [Y\leq 12{,}14]=\mathbb {P} \left[{\frac {Y-10}{2}}\leq {\frac {12{,}14-10}{2}}\right]=\mathbb {P} [X\leq 1{,}07]=\Phi (1{,}07)\approx 0{,}85769}$, pour ${\displaystyle Y\sim {\mathcal {N}}(10{,}2^{2})}$.

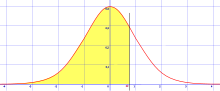
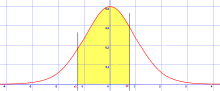
La table de valeurs permet également d'obtenir la probabilité qu'une variable aléatoire de loi normale ${\displaystyle X\sim {\mathcal {N}}(0,1)}$ appartienne à un intervalle donné [a , b] par la formule : ${\displaystyle \mathbb {P} \left[X\in [a,b]\right]=\mathbb {P} [X\leq b]-\mathbb {P} [X<a]=\Phi (b)-\Phi (a)}$. Par exemple :

• ${\displaystyle \mathbb {P} [X\geq 1{,}07]=1-\mathbb {P} [X<1{,}07]=1-\mathbb {P} [X\leq 1{,}07]\approx 0{,}14231}$ pour ${\displaystyle X\sim {\mathcal {N}}(0,1)}$ ;
• ${\displaystyle \mathbb {P} [0\leq X\leq 1{,}07]=\Phi (1{,}07)-\Phi (0)=\Phi (1{,}07)-0{,}5\approx 0{,}85769-0{,}5=0{,}35769}$ pour ${\displaystyle X\sim {\mathcal {N}}(0,1)}$.

Plages de normalité, intervalles de confiance[modifier | modifier le code]

Un des intérêts de calculer des probabilités sur des intervalles est l'utilisation des intervalles de confiance pour les tests statistiques. Une loi normale est définie par deux valeurs : sa moyenne μ et son écart type σ. Ainsi il est utile de s'intéresser aux intervalles^[52] du type [μ – rσ, μ + rσ]. ${\displaystyle \mathbb {P} [\mu -r\sigma \leq Y\leq \mu +r\sigma ]=\Phi (r)-(1-\Phi (r))=2\Phi (r)-1}$ pour ${\displaystyle Y\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$.

Table de valeurs des intervalles de confiance

La table suivante s'obtient grâce aux tables précédentes^[52] et donne les probabilités : ${\displaystyle \mathbb {P} _{r}=\mathbb {P} [\mu -r\sigma \leq Y\leq \mu +r\sigma ]=2\Phi (r)-1{\text{ pour }}Y\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$.

Table de valeurs des intervalles de confiance

r	0,0	0,5	1,0	1,5	2,0	2,5	3,0	3,5
${\displaystyle \mathbb {P} _{r}}$	0,00	0,3829	0,6827	0,8664	0,9545	0,9876	0,9973	0,9995