Fonction hyperbolique — Wikipédia

En mathématiques, on appelle fonctions hyperboliques les fonctions cosinus hyperbolique, sinus hyperbolique et tangente hyperbolique. Les noms « sinus », « cosinus » et « tangente » proviennent de leur ressemblance avec les fonctions trigonométriques (dites « circulaires » car en relation avec le cercle unité $x 2 + y 2 = 1$ ) et le terme « hyperbolique » provient de leur relation avec l'hyperbole d'équation $x 2 - y 2 = 1$ .

Elles sont utilisées en analyse pour le calcul intégral, la résolution des équations différentielles mais aussi en géométrie hyperbolique.

Histoire[modifier | modifier le code]

Les fonctions hyperboliques ont été inventées par le jésuite Vincenzo Riccati dans les années 1760 alors qu'il cherchait, avec son collègue Saladini, à calculer l'aire sous l'hyperbole d'équation x² – y² = 1. La méthode géométrique qu'il employa alors était très similaire à celle que l'on peut utiliser pour calculer l'aire d'un cercle d'équation $x 2 + y 2 = 1$ . Le calcul de l'aire du cercle fait intervenir les fonctions trigonométriques classiques que Riccati nommait cosinus et sinus circulaires. Par analogie, il appela alors les fonctions qu'il venait de créer cosinus et sinus hyperboliques. Ce fut un choix heureux, car cette ressemblance ne s'arrête pas à la méthode de calcul d'aire mais aussi à toutes les formules trigonométriques. Cependant, pourtant au fait du travail de son contemporain Euler, il n'utilisa pas la fonction exponentielle pour les définir mais seulement des considérations géométriques. L'autre grand mathématicien ayant étudié les fonctions hyperboliques est Jean-Henri Lambert, qui en fit une étude complète en 1770. Cette quasi-simultanéité fait que l'on attribue parfois à Lambert la paternité des fonctions hyperboliques, bien que les écrits de Riccati soient antérieurs de quelques années.

Définitions[modifier | modifier le code]

Les fonctions hyperboliques sont analogues aux fonctions trigonométriques ou fonctions circulaires. Ce sont les fonctions :

Sinus hyperbolique[modifier | modifier le code]

Article détaillé : Sinus hyperbolique.

Définie comme étant la partie impaire de la fonction exponentielle, c’est-à-dire par :

\operatorname {sinh} (x)={\frac {{\rm {e}}^{x}-{\rm {e}}^{-x}}{2}}

La fonction $sinh$ — ou $sh$ — est une bijection de classe $C \infty$ de ℝ sur ℝ strictement croissante, et impaire. Sa dérivée est le cosinus hyperbolique. Son application réciproque est l'argument sinus hyperbolique.

Cosinus hyperbolique[modifier | modifier le code]

Article détaillé : Cosinus hyperbolique.

Définie comme étant la partie paire de la fonction exponentielle, c’est-à-dire par :

\operatorname {cosh} (x)={\frac {{\rm {e}}^{x}+{\rm {e}}^{-x}}{2}}

La fonction $cosh$ — ou $ch$ — est une application de ℝ dans $[1, +\infty[$ strictement croissante sur ℝ⁺, et paire. La fonction $cosh$ est de classe $C \infty$ sur ℝ et sa dérivée est le sinus hyperbolique. Sa restriction à ℝ⁺ est une bijection à valeurs dans $[1, +\infty[$ dont l'application réciproque est l'argument cosinus hyperbolique.

Tangente hyperbolique[modifier | modifier le code]

Article détaillé : Tangente hyperbolique.

Définie par :

\operatorname {tanh} (x)={\frac {\operatorname {sinh} (x)}{\operatorname {cosh} (x)}}={\frac {{\rm {e}}^{x}-{\rm {e}}^{-x}}{{\rm {e}}^{x}+{\rm {e}}^{-x}}}={\frac {{\rm {e}}^{2x}-1}{{\rm {e}}^{2x}+1}}=1-{\frac {2}{{\rm {e}}^{2x}+1}}

La fonction $tanh$ — ou $th$ — est une bijection de classe $C \infty$ de ℝ sur $]-1, 1[$ strictement croissante, et impaire. Sa dérivée est ${\frac {1}{\operatorname {cosh} ^{2}}}=1-\operatorname {tanh} ^{2}$ . Son application réciproque est l'argument tangente hyperbolique.

Cotangente hyperbolique[modifier | modifier le code]

Définie par :

\coth(x)={\frac {\operatorname {cosh} (x)}{\operatorname {sinh} (x)}}={\frac {{\rm {e}}^{x}+{\rm {e}}^{-x}}{{\rm {e}}^{x}-{\rm {e}}^{-x}}}={\frac {{\rm {e}}^{2x}+1}{{\rm {e}}^{2x}-1}}

$coth$ est une bijection de classe $C \infty$ de ℝ* dans $]-\infty, -1[\cup]1, +\infty[$ . Sa dérivée est ${\frac {-1}{\operatorname {sinh} ^{2}}}=1-\coth ^{2}$ . Son application réciproque est l'argument cotangente hyperbolique.

Sécante hyperbolique[modifier | modifier le code]

Définie par :

\forall x\in \mathbb {R} ,\quad \operatorname {sech} (x)={\frac {1}{\operatorname {cosh} (x)}}

Cosécante hyperbolique[modifier | modifier le code]

Définie par :

\forall x\in \mathbb {R} ^{*},\quad \operatorname {csch} (x)={\frac {1}{\operatorname {sinh} (x)}}

Tableau de variations[modifier | modifier le code]

Les fonctions $sinh$ , $tanh$ et $coth$ sont impaires et la fonction $cosh$ est paire, on peut donc réduire leur domaine d'étude à $[0, +\infty[$ .

$x$	0		$+\infty$
$cosh x$	1	$\nearrow$	$+\infty$
$sinh x$	0	$\nearrow$	$+\infty$
$tanh x$	0	$\nearrow$	+1
coth x	$+\infty$	$\searrow$	+1

Propriétés[modifier | modifier le code]

Par construction, ${\rm {e}}^{x}=\operatorname {cosh} (x)+\operatorname {sinh} (x)\quad {\rm {et}}\quad {\rm {e}}^{-x}=\operatorname {cosh} (x)-\operatorname {sinh} (x).$

On en déduit la formule suivante :

\operatorname {cosh} ^{2}x-\operatorname {sinh} ^{2}x=1.

De même que les points $(cos x, sin x)$ décrivent un cercle lorsque $x$ parcourt ℝ, les points $(cosh x, sinh x)$ décrivent une branche d'hyperbole.

Le paramètre $x$ ne peut pas être interprété comme un angle, ni comme une longueur d'arc ; les fonctions hyperboliques sont périodiques, mais de période imaginaire pure.

La fonction $cosh$ admet 1 pour minimum, en 0.

La fonction $sinh$ est impaire et ainsi $sinh(0) = 0$ .

Les fonctions hyperboliques satisfont à des relations très ressemblantes aux identités trigonométriques. En fait, la règle d'Osborn^[1] dit que l'on peut convertir n'importe quelle identité trigonométrique en une identité hyperbolique en la développant complètement à l'aide de puissances entières de sinus et cosinus, changeant $sin$ en $sinh$ et $cos$ en $cosh$ , et remplaçant le signe de chaque terme qui contient un produit de deux sinus en son opposé.

Cela nous permet d'obtenir par exemple, les formules d'addition et de soustraction :

\operatorname {sinh} (x+y)=\operatorname {sinh} (x)\,\operatorname {cosh} (y)+\operatorname {cosh} (x)\,\operatorname {sinh} (y)

\operatorname {cosh} (x+y)=\operatorname {cosh} (x)\,\operatorname {cosh} (y)+\operatorname {sinh} (x)\,\operatorname {sinh} (y)

\operatorname {sinh} (x-y)=\operatorname {sinh} (x)\,\operatorname {cosh} (y)-\operatorname {cosh} (x)\,\operatorname {sinh} (y)

\operatorname {cosh} (x-y)=\operatorname {cosh} (x)\,\operatorname {cosh} (y)-\operatorname {sinh} (x)\,\operatorname {sinh} (y)

et des « formules d'angle moitié » (la deuxième étant valide si $x$ est positif ou nul) :

\operatorname {cosh} \left({\frac {x}{2}}\right)={\sqrt {\frac {\operatorname {cosh} (x)+1}{2}}}

\operatorname {sinh} \left({\frac {x}{2}}\right)={\sqrt {\frac {\operatorname {cosh} (x)-1}{2}}}

De ces expressions on déduit les formules suivantes relatives à la tangente hyperbolique : $1-\operatorname {tanh} ^{2}(x)={\frac {1}{\operatorname {cosh} ^{2}(x)}},\quad \operatorname {tanh} (x+y)={\frac {\operatorname {tanh} (x)+\operatorname {tanh} (y)}{1+\operatorname {tanh} (x)\,\operatorname {tanh} (y)}},\quad \operatorname {tanh} \left({\frac {x}{2}}\right)={\sqrt {\frac {\operatorname {cosh} (x)-1}{\operatorname {cosh} (x)+1}}}.$

On a de même :

\operatorname {sinh} (2x)=2\,\operatorname {cosh} (x)\,\operatorname {sinh} (x),

\operatorname {cosh} (2x)=\operatorname {cosh} ^{2}(x)+\operatorname {sinh} ^{2}(x)=1+2\,\operatorname {sinh} ^{2}(x)=2\,\operatorname {cosh} ^{2}(x)-1,

\operatorname {tanh} (2x)={\frac {2\,\operatorname {tanh} (x)}{\operatorname {tanh} ^{2}(x)+1}}.

La fonction cosinus hyperbolique est convexe. Elle intervient dans la définition de la chaînette, laquelle correspond à la forme que prend un câble suspendu à ses extrémités et soumis à son propre poids.

Puisque la fonction exponentielle peut être prolongée à l'ensemble des nombres complexes, nous pouvons aussi étendre les définitions des fonctions hyperboliques à l'ensemble des nombres complexes. Les fonctions sinus hyperbolique et cosinus hyperbolique sont alors holomorphes et même entières.

Applications réciproques[modifier | modifier le code]

Argument sinus hyperbolique[modifier | modifier le code]

Article détaillé : Sinus hyperbolique réciproque.

$arsinh$ — ou $argsh$ ^[2] — est l'application réciproque de $sinh$ . C'est une bijection de ℝ sur ℝ, impaire et strictement croissante. La fonction $arsinh$ est dérivable sur ℝ et sa dérivée est $x\mapsto {\tfrac {1}{\sqrt {x^{2}+1}}}$ . La fonction $arsinh$ admet la forme logarithmique suivante :

\operatorname {arsinh} x=\ln \left(x+{\sqrt {x^{2}+1}}\right)

.

Argument cosinus hyperbolique[modifier | modifier le code]

Article détaillé : Cosinus hyperbolique réciproque.

$arcosh$ — ou $argch$ ^[3] — est l'application réciproque de la restriction de $cosh$ à ℝ⁺. C'est une bijection de $[1, +\infty[$ sur ℝ⁺, strictement croissante. La fonction $arcosh$ est dérivable sur $]1, +\infty[$ et sa dérivée est $x\mapsto {\tfrac {1}{\sqrt {x^{2}-1}}}$ . La fonction $arcosh$ admet une forme logarithmique :

\operatorname {arcosh} x=\ln \left(x+{\sqrt {x^{2}-1}}\right)

.

Argument tangente hyperbolique[modifier | modifier le code]

Article détaillé : Tangente hyperbolique réciproque.

$artanh$ — ou $argth$ ^[4] — est l'application réciproque de $tanh$ . C'est une bijection de $]-1, 1[$ sur ℝ, impaire, strictement croissante. La fonction $artanh$ est dérivable sur $]-1, 1[$ et sa dérivée est $x\mapsto {\tfrac {1}{1-x^{2}}}$ . La fonction $artanh$ admet une forme logarithmique :

\operatorname {artanh} x={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)

.

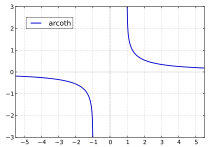
Argument cotangente hyperbolique[modifier | modifier le code]

$arcoth$ — ou $argcoth$ ^[5] — est l'application réciproque de $coth$ . C'est une bijection de $]-\infty, -1[\cup]1, +\infty[$ sur ℝ*. La fonction $arcoth$ est dérivable sur $]-\infty, -1[\cup]1, +\infty[$ et sa dérivée est $x\mapsto {\tfrac {1}{1-x^{2}}}$ . La fonction $arcoth$ admet une forme logarithmique :

\operatorname {arcoth} x={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right)

.

Argument sécante hyperbolique[modifier | modifier le code]

$arsech$ — ou $argsech$ est l'application réciproque de sech.

\forall x\in \left]0,1\right]\quad \operatorname {arsech} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)=\ln \left({\frac {1+{\sqrt {1-x^{2}}}}{x}}\right)

.

Argument cosécante hyperbolique[modifier | modifier le code]

$arcsch$ — ou $argcsch$ est l'application réciproque de csch.

\forall x\in \mathbb {R} ^{*}\quad \operatorname {arcsch} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right)=\ln \left({\frac {1+{\sqrt {1+x^{2}}}}{x}}\right)

.

Relations entre fonctions hyperboliques et fonctions circulaires[modifier | modifier le code]

Des formules d'Euler, on déduit immédiatement :

\cos(x)=\operatorname {cosh} (\mathrm {i} x)

\mathrm {i} \sin(x)=\operatorname {sinh} (\mathrm {i} x)

ou encore :

\operatorname {cosh} (x)=\cos(\mathrm {i} x)

\operatorname {sinh} (x)=-\mathrm {i} \,\sin(\mathrm {i} x).

D'autres relations entre fonctions hyperboliques et circulaires sont données par la fonction de Gudermann ou gudermannien. Elles ont été explicitées par le mathématicien Christoph Gudermann. Le gudermannien $θ$ de $t$ peut être défini par $tan θ = sinh t$ . On en déduit de nombreuses relations entre les fonctions trigonométriques de $θ$ et les fonctions hyperboliques de $t$ . Par exemple :

{\frac {1}{\operatorname {cosh} (t)}}=\cos \theta

\operatorname {tanh} (t)=\sin \theta .

dt={\frac {d\theta }{\cos \theta }}

Utilisation en géométrie hyperbolique[modifier | modifier le code]

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Les formules de la trigonométrie sphérique restent valables en géométrie hyperbolique en remplaçant partout cos par cosh, sin par sinh et tan par tanh, et en n'oubliant pas de changer les signes correspondant à des produits d'un nombre pair de fonctions sin ou tan.

Relations lorsque l'argument est imaginaire pur[modifier | modifier le code]

Fonctions trigonométriques
Écriture	Expression	Ensemble de départ	Ensemble d'arrivée	Dérivée	Argument complexe
$\sin x$	${\frac {\mathrm {e} ^{\mathrm {i} \,y}-\mathrm {e} ^{-\mathrm {i} \,y}}{2\,\mathrm {i} }}$	$\mathbb {R}$	$[-1;1]$	$\cos x$	$\sin \left(\mathrm {i} x\right)=\mathrm {i} \operatorname {sinh} x$
$\cos x$	${\frac {\mathrm {e} ^{\mathrm {i} \,y}+\mathrm {e} ^{-\mathrm {i} \,y}}{2}}$	$\mathbb {R}$	$[-1;1]$	$-\sin x$	$\cos \left(\mathrm {i} x\right)=\operatorname {cosh} x$
$\tan x$	$-\mathrm {i} {\frac {\mathrm {e} ^{\mathrm {i} \,y}-\mathrm {e} ^{-\mathrm {i} \,y}}{\mathrm {e} ^{\mathrm {i} \,y}+\mathrm {e} ^{-\mathrm {i} \,y}}}$	$\mathbb {R} \backslash \left\{{\tfrac {\pi }{2}}+p\,\pi \right\}\;,\;p\in \mathbb {Z}$	$\mathbb {R}$	$1+\tan ^{2}x={\frac {1}{\cos ^{2}x}}$	$\tan \left(\mathrm {i} x\right)=\mathrm {i} \operatorname {tanh} x$
$\cot x$	$\mathrm {i} {\frac {\mathrm {e} ^{\mathrm {i} \,y}+\mathrm {e} ^{-\mathrm {i} \,y}}{\mathrm {e} ^{\mathrm {i} \,y}-\mathrm {e} ^{-\mathrm {i} \,y}}}$	$\mathbb {R} \backslash \left\{p\,\pi \right\}\;,\;p\in \mathbb {Z}$	$\mathbb {R}$	$-\left(1+\cot ^{2}x\right)=-{\frac {1}{\sin ^{2}x}}$	$\cot \left(\mathrm {i} x\right)=-\mathrm {i} \operatorname {coth} x$
$\sec x$	${\frac {2}{\mathrm {e} ^{\mathrm {i} \,y}+\mathrm {e} ^{-\mathrm {i} \,y}}}$	$\mathbb {R} \backslash \left\{{\tfrac {\pi }{2}}+p\,\pi \right\}\;,\;p\in \mathbb {Z}$	$\mathbb {R} \backslash ]-1;1[$	${\frac {\sin x}{\cos ^{2}x}}=\sin x\cdot \tan x$	$\sec \left(\mathrm {i} x\right)=\operatorname {sech} x$
$\csc x$	${\frac {2\,\mathrm {i} }{\mathrm {e} ^{\mathrm {i} \,y}-\mathrm {e} ^{-\mathrm {i} \,y}}}$	$\mathbb {R} \backslash \left\{p\,\pi \right\}\rightarrow \;,\;p\in \mathbb {Z}$	$\mathbb {R} \backslash ]-1;1[$	$-{\frac {\cos x}{\sin ^{2}x}}=-\cos x\cdot \cot x$	$\csc \left(\mathrm {i} x\right)=-\mathrm {i} \operatorname {csch} x$

Fonctions trigonométriques réciproques
Écriture	Expression	Ensemble de départ	Ensemble d'arrivée	Dérivée	Argument complexe
$\arcsin x$	$\mathrm {i} \ln \left({\sqrt {1-x^{2}}}-\mathrm {i} x\right)$	$[-1;1]$	$\left[-{\tfrac {\pi }{2}};{\tfrac {\pi }{2}}\right]$	${\frac {1}{\sqrt {1-x^{2}}}}$	$\arcsin \left(\mathrm {i} x\right)=\mathrm {i} \operatorname {arsinh} x$
$\arccos x$	$\mathrm {i} \ln \left(x-\mathrm {i} {\sqrt {1-x^{2}}}\right)$	$[-1;1]$	$\left[0;\pi \right]$	$-{\frac {1}{\sqrt {1-x^{2}}}}$	$\arccos \left(\mathrm {i} x\right)={\tfrac {\pi }{2}}-\mathrm {i} \operatorname {arsinh} x$
$\arctan x$	${\frac {\mathrm {i} }{2}}\ln {\frac {1-\mathrm {i} \,x}{1+\mathrm {i} \,x}}$	$\mathbb {R}$	$\left]-{\tfrac {\pi }{2}};{\tfrac {\pi }{2}}\right[$	${\frac {1}{1+x^{2}}}$	$\arctan \left(\mathrm {i} x\right)=\mathrm {i} \operatorname {artanh} x$
$\operatorname {arccot} x$	${\frac {\mathrm {i} }{2}}\ln {\frac {x-\mathrm {i} }{x+\mathrm {i} }}$	$\mathbb {R}$	$\left]0;\pi \right[$	$-{\frac {1}{1+x^{2}}}$	$\operatorname {arccot} \left(\mathrm {i} x\right)=-\mathrm {i} \operatorname {arcoth} x$
$\operatorname {arcsec} x$	$\mathrm {i} \ln \left({\tfrac {1}{x}}-\mathrm {i} {\sqrt {1-{\tfrac {1}{x^{2}}}}}\right)$	$\mathbb {R} \backslash ]-1;1[$	$\left[0;{\tfrac {\pi }{2}}\right[\cup \left]{\tfrac {\pi }{2}};\pi \right]$	${\frac {1}{x^{2}{\sqrt {1-{\tfrac {1}{x^{2}}}}}}}$	$\operatorname {arcsec} \left(\mathrm {i} x\right)={\tfrac {\pi }{2}}+\mathrm {i} \operatorname {arcsch} x$
$\operatorname {arccsc} x$	$\mathrm {i} \ln \left({\sqrt {1-{\tfrac {1}{x^{2}}}}}-{\tfrac {\mathrm {i} }{x}}\right)$	$\mathbb {R} \backslash ]-1;1[$	$\left[-{\tfrac {\pi }{2}};0\right[\cup \left]0;{\tfrac {\pi }{2}}\right]$	$-{\frac {1}{x^{2}{\sqrt {1-{\frac {1}{x^{2}}}}}}}$	$\operatorname {arccsc} \left(\mathrm {i} x\right)=-\mathrm {i} \operatorname {arcsch} x$

Démonstration

\left.{\begin{matrix}x=\sin y={\frac {\mathrm {e} ^{\mathrm {i} \,y}-\mathrm {e} ^{-\mathrm {i} \,y}}{2\,\mathrm {i} }}\Rightarrow \mathrm {e} ^{2\,\mathrm {i} \,y}-2\,\mathrm {i} \,x\,\mathrm {e} ^{\mathrm {i} \,y}-1=0\Rightarrow y=-\mathrm {i} \ln \left(\mathrm {i} x\pm {\sqrt {1-x^{2}}}\right)\\\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \arcsin x\in \left[-{\tfrac {\pi }{2}};{\tfrac {\pi }{2}}\right]\end{matrix}}\right\}\Rightarrow \arcsin x=-\mathrm {i} \ln \left(\mathrm {i} x+{\sqrt {1-x^{2}}}\right)=\mathrm {i} \ln \left({\sqrt {1-x^{2}}}-\mathrm {i} x\right)

\left.{\begin{matrix}x=\cos y={\frac {\mathrm {e} ^{\mathrm {i} \,y}+\mathrm {e} ^{-\mathrm {i} \,y}}{2}}\Rightarrow \mathrm {e} ^{2\,\mathrm {i} \,y}-2\;\;x\,\mathrm {e} ^{\mathrm {i} \,y}+1=0\Rightarrow y=-\mathrm {i} \ln \left(x\pm \mathrm {i} {\sqrt {1-x^{2}}}\right)\\\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \arccos x\in \left[0;\pi \right]\end{matrix}}\right\}\Rightarrow \arccos x=-\mathrm {i} \ln \left(x+\mathrm {i} {\sqrt {1-x^{2}}}\right)=\mathrm {i} \ln \left(x-\mathrm {i} {\sqrt {1-x^{2}}}\right)

\,x=\tan y=-\mathrm {i} {\frac {\mathrm {e} ^{\mathrm {i} \,y}-\mathrm {e} ^{-\mathrm {i} \,y}}{\mathrm {e} ^{\mathrm {i} \,y}+\mathrm {e} ^{-\mathrm {i} \,y}}}\Rightarrow \mathrm {e} ^{2\,\mathrm {i} \,y}={\frac {\mathrm {i} -x}{\mathrm {i} +x}}\Rightarrow y=-{\frac {\mathrm {i} }{2}}\ln {\frac {\mathrm {i} -x}{\mathrm {i} +x}}={\frac {\mathrm {i} }{2}}\ln {\frac {1-\mathrm {i} x}{1+\mathrm {i} x}}\Rightarrow \arctan x={\frac {\mathrm {i} }{2}}\ln {\frac {1-\mathrm {i} x}{1+\mathrm {i} x}}

\,x=\cot y=\;\;\;\mathrm {i} {\frac {\mathrm {e} ^{\mathrm {i} \,y}+\mathrm {e} ^{-\mathrm {i} \,y}}{\mathrm {e} ^{\mathrm {i} \,y}-\mathrm {e} ^{-\mathrm {i} \,y}}}\Rightarrow \mathrm {e} ^{2\,\mathrm {i} \,y}={\frac {x+\mathrm {i} }{x-\mathrm {i} }}\Rightarrow y=-{\frac {\mathrm {i} }{2}}\ln {\frac {x+\mathrm {i} }{x-\mathrm {i} }}={\frac {\mathrm {i} }{2}}\ln {\frac {x-\mathrm {i} }{x+\mathrm {i} }}\Rightarrow \operatorname {arccot} x={\frac {\mathrm {i} }{2}}\ln {\frac {x-\mathrm {i} }{x+\mathrm {i} }}

\left.{\begin{matrix}x=\sec y={\frac {2}{\mathrm {e} ^{\mathrm {i} \,y}+\mathrm {e} ^{-\mathrm {i} \,y}}}\Rightarrow x\,\mathrm {e} ^{2\,\mathrm {i} \,y}-2\;\;\mathrm {e} ^{\mathrm {i} \,y}+x=0\Rightarrow y=-\mathrm {i} \ln \left({\frac {1}{x}}\pm \mathrm {i} {\sqrt {1-{\frac {1}{x^{2}}}}}\right)\\\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \operatorname {arcsec} x\in [0;\pi ]\end{matrix}}\right\}\Rightarrow \operatorname {arcsec} x=-\mathrm {i} \ln \left({\frac {1}{x}}+\mathrm {i} {\sqrt {1-{\frac {1}{x^{2}}}}}\right)=\mathrm {i} \ln \left({\frac {1}{x}}-\mathrm {i} {\sqrt {1-{\frac {1}{x^{2}}}}}\right)

\left.{\begin{matrix}x=\csc y={\frac {2\,\mathrm {i} }{\mathrm {e} ^{\mathrm {i} \,y}-\mathrm {e} ^{-\mathrm {i} \,y}}}\Rightarrow x\,\mathrm {e} ^{2\,\mathrm {i} \,y}-2\,\mathrm {i} \,\mathrm {e} ^{\mathrm {i} \,y}-x=0\Rightarrow y=-\mathrm {i} \ln \left({\frac {\mathrm {i} }{x}}\pm {\sqrt {1-{\frac {1}{x^{2}}}}}\right)\\\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \operatorname {arccsc} x\in \left[-{\tfrac {\pi }{2}};{\tfrac {\pi }{2}}\right]\end{matrix}}\right\}\Rightarrow \operatorname {arccsc} x=-\mathrm {i} \ln \left({\sqrt {1-{\frac {1}{x^{2}}}}}+{\frac {\mathrm {i} }{x}}\right)=\mathrm {i} \ln \left({\sqrt {1-{\frac {1}{x^{2}}}}}-{\frac {\mathrm {i} }{x}}\right)

Fonctions hyperboliques
Écriture	Expression	Ensemble de départ	Ensemble d'arrivée	Dérivée	Argument complexe
$\operatorname {sinh} x=\operatorname {sh} x$	${\frac {{\mathrm {e} }^{x}-{\mathrm {e} }^{-x}}{2}}$	$\mathbb {R}$	$\mathbb {R}$	$\operatorname {cosh} x$	$\operatorname {sinh} (\mathrm {i} x)=\mathrm {i} \sin x$
$\operatorname {cosh} x=\operatorname {ch} x$	${\frac {{\mathrm {e} }^{x}+{\mathrm {e} }^{-x}}{2}}$	$\mathbb {R}$	$[1;\infty [$	$\operatorname {sinh} x$	$\operatorname {cosh} (\mathrm {i} x)=\cos x$
$\operatorname {tanh} x=\operatorname {th} x$	${\frac {{\mathrm {e} }^{x}-{\mathrm {e} }^{-x}}{{\mathrm {e} }^{x}+{\mathrm {e} }^{-x}}}$	$\mathbb {R}$	$]-1;1[$	${\frac {1}{\operatorname {cosh} ^{2}x}}=1-\operatorname {tanh} ^{2}x$	$\operatorname {tanh} (\mathrm {i} x)=\mathrm {i} \tan x$
$\operatorname {coth} x$	${\frac {{\mathrm {e} }^{x}+{\mathrm {e} }^{-x}}{{\mathrm {e} }^{x}-{\mathrm {e} }^{-x}}}$	$\mathbb {R} ^{*}$	$\mathbb {R} \backslash [-1;1]$	$-{\frac {1}{\operatorname {sinh} ^{2}x}}=1-\operatorname {coth} ^{2}x$	$\operatorname {coth} (\mathrm {i} x)=-\mathrm {i} \cot x$
$\operatorname {sech} x$	${\frac {2}{{\mathrm {e} }^{x}+{\mathrm {e} }^{-x}}}$	$\mathbb {R}$	$]0;1]$	$-{\frac {\operatorname {sinh} x}{\operatorname {cosh} ^{2}x}}$	$\operatorname {sech} (\mathrm {i} x)=\sec x$
$\operatorname {csch} x$	${\frac {2}{{\mathrm {e} }^{x}-{\mathrm {e} }^{-x}}}$	$\mathbb {R} ^{*}$	$\mathbb {R} ^{*}$	$-{\frac {\operatorname {cosh} x}{\operatorname {sinh} ^{2}x}}$	$\operatorname {csch} (\mathrm {i} x)=-\mathrm {i} \csc x$

Fonctions hyperboliques réciproques
Écriture	Expression	Ensemble de départ	Ensemble d'arrivée	Dérivée	Argument complexe
$\operatorname {arsinh} x=\operatorname {argsh} x$	$\ln \left(x+{\sqrt {x^{2}+1}}\right)$	$\mathbb {R}$	$\mathbb {R}$	${\frac {1}{\sqrt {x^{2}+1}}}$	$\operatorname {arsinh} (\mathrm {i} x)=\mathrm {i} \arcsin x$
$\operatorname {arcosh} x=\operatorname {argch} x$	$\ln \left(x+{\sqrt {x^{2}-1}}\right)$	$[1;\infty [$	$\mathbb {R} ^{+}$	${\frac {1}{\sqrt {x^{2}-1}}}$	$\operatorname {arcosh} (\mathrm {i} x)=\operatorname {arsinh} x+\mathrm {i} {\tfrac {\pi }{2}}$ ^{[Note 1]}^[6]
$\operatorname {artanh} x=\operatorname {argth} x$	${\frac {1}{2}}\ln {\frac {1+x}{1-x}}$	$]-1;1[$	$\mathbb {R}$	${\frac {1}{1-x^{2}}}$	$\operatorname {artanh} (\mathrm {i} x)=\mathrm {i} \arctan x$
$\operatorname {arcoth} x=\operatorname {argcoth} x$	${\frac {1}{2}}\ln {\frac {x+1}{x-1}}$	$\mathbb {R} \backslash [-1;1]$	$\mathbb {R} ^{*}$	${\frac {1}{1-x^{2}}}$	$\operatorname {arcoth} (\mathrm {i} x)=-\mathrm {i} \operatorname {arccot} x$
$\operatorname {arsech} x=\operatorname {argsech} x$	$\ln {\frac {1+{\sqrt {1-x^{2}}}}{x}}$	$]0;1]$	$\mathbb {R} ^{+}$	$-{\frac {1}{x{\sqrt {1-x^{2}}}}}$	$\operatorname {arsech} (\mathrm {i} x)=\operatorname {arcsch} x-\mathrm {i} {\tfrac {\pi }{2}}$ ^{[Note 1]}^[7]
$\operatorname {arcsch} x=\operatorname {argcsch} x$	$\ln {\frac {1+{\sqrt {1+x^{2}}}}{x}}$	$\mathbb {R} ^{*}$	$\mathbb {R} ^{*}$	$-{\frac {1}{x{\sqrt {1+x^{2}}}}}$	$\operatorname {arcsch} (\mathrm {i} x)=-\mathrm {i} \operatorname {arccsc} x$

Démonstration

\left.{\begin{matrix}x=\sinh y={\frac {\mathrm {e} ^{y}-\mathrm {e} ^{-y}}{2}}\Rightarrow \mathrm {e} ^{2\,y}-2\,x\,\mathrm {e} ^{y}-1=0\Rightarrow y=\ln \left(x\pm {\sqrt {x^{2}+1}}\right)\\\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad x\pm {\sqrt {x^{2}+1}}\geqslant 0\end{matrix}}\right\}\Rightarrow \operatorname {arcsinh} x=\ln \left(x+{\sqrt {x^{2}+1}}\right)

\left.{\begin{matrix}x=\cosh y={\frac {\mathrm {e} ^{y}+\mathrm {e} ^{-y}}{2}}\Rightarrow \mathrm {e} ^{2\,y}-2\,x\,\mathrm {e} ^{y}+1=0\Rightarrow y=\ln \left(x\pm {\sqrt {x^{2}-1}}\right)\\\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad {\text{bijection : }}\operatorname {arccosh} x\geqslant 0\end{matrix}}\right\}\Rightarrow \operatorname {arccosh} x=\ln \left(x+{\sqrt {x^{2}-1}}\right)

\,x=\tanh y={\frac {\mathrm {e} ^{y}-\mathrm {e} ^{-y}}{\mathrm {e} ^{y}+\mathrm {e} ^{-y}}}\Rightarrow \mathrm {e} ^{2\,y}={\frac {1-x}{1+x}}\Rightarrow y={\frac {1}{2}}\ln {\frac {1-x}{1+x}}\Rightarrow \operatorname {arctanh} x={\frac {1}{2}}\ln {\frac {1-x}{1+x}}

\,x=\coth y={\frac {\mathrm {e} ^{y}+\mathrm {e} ^{-y}}{\mathrm {e} ^{y}-\mathrm {e} ^{-y}}}\Rightarrow \mathrm {e} ^{2\,y}={\frac {x+1}{x-1}}\Rightarrow y={\frac {1}{2}}\ln {\frac {x+1}{x-1}}\Rightarrow \operatorname {arccoth} x={\frac {1}{2}}\ln {\frac {x+1}{x-1}}

\left.{\begin{matrix}x=\operatorname {sech} y={\frac {2}{\mathrm {e} ^{y}+\mathrm {e} ^{-y}}}\Rightarrow x\,\mathrm {e} ^{2\,y}-2\,\mathrm {e} ^{y}+x=0\Rightarrow y=\ln \left({\frac {1}{x}}\pm {\sqrt {{\frac {1}{x^{2}}}-1}}\right)=\ln {\frac {1\pm {\sqrt {1-x^{2}}}}{x}}\\\qquad {\frac {1\pm {\sqrt {1-x^{2}}}}{x}}\geqslant 1\Leftrightarrow 1-x\geqslant \mp {\sqrt {1-x^{2}}}\Leftrightarrow {\sqrt {\left(1-x\right)\left(1-x\right)}}\geqslant \mp {\sqrt {\left(1-x\right)\left(1+x\right)}}\end{matrix}}\right\}\Rightarrow \operatorname {arsech} x=\ln {\tfrac {1+{\sqrt {1-x^{2}}}}{x}}

\left.{\begin{matrix}x=\operatorname {csch} y={\frac {2}{\mathrm {e} ^{y}-\mathrm {e} ^{-y}}}\Rightarrow x\,\mathrm {e} ^{2\,y}-2\,\mathrm {e} ^{y}-x=0\Rightarrow y=\ln \left({\frac {1}{x}}\pm {\sqrt {{\frac {1}{x^{2}}}+1}}\right)=\ln {\frac {1\pm {\sqrt {1+x^{2}}}}{x}}\\\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {\frac {1}{x}}\pm {\sqrt {{\frac {1}{x^{2}}}+1}}>0\end{matrix}}\right\}\Rightarrow {\begin{cases}\operatorname {arcsch} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right)\\\qquad \quad \;\;\,=\ln {\frac {1+\operatorname {sgn} (x){\sqrt {1+x^{2}}}}{x}}\end{cases}}

Note :

↑ ^{a et b} si le choix de la détermination de l'angle du logarithme complexe est $[0;2\pi [$ , c.-à-d. si $\ln z=|z|+\mathrm {i} \,\theta$ avec $\theta \in [0;2\pi [$

Notes et références[modifier | modifier le code]

↑ (en) Eric W. Weisstein, « Osborn's Rule », sur MathWorld.
↑ La norme ISO 31-11 recommande la notation « arsinh » pour cette fonction.
↑ La norme ISO 31-11 recommande la notation « arcosh » pour cette fonction.
↑ La norme ISO 31-11 recommande la notation « artanh » pour cette fonction.
↑ La norme ISO 31-11 recommande la notation « arcoth » pour cette fonction.
↑ $\operatorname {arcosh} \left(\mathrm {i} x\right)$ et $\operatorname {arsinh} x$ sur wolframalpha.com. La courbe correspond à $\operatorname {arcosh} (\mathrm {i} x)=\operatorname {sgn} x\cdot \left(\operatorname {arsinh} x+\mathrm {i} {\tfrac {\pi }{2}}\right)$ .
↑ $\operatorname {arsech} \left(\mathrm {i} x\right)$ et $\operatorname {arcsch} x$ sur wolframalpha.com. La courbe correspond à $\operatorname {arsech} (\mathrm {i} x)=\operatorname {sgn} x\cdot \left(\operatorname {arcsch} x-\mathrm {i} {\tfrac {\pi }{2}}\right)$ .

Voir aussi[modifier | modifier le code]

Sur les autres projets Wikimedia :

Trigonométrie hyperbolique, sur Wikiversity

Articles connexes[modifier | modifier le code]

Lien externe[modifier | modifier le code]

(en) « Vincent Riccati, S.J. (1707 - 1775) and his hyperbolic functions »

Portail de l'analyse

[ln-6] {a et b} si le choix de la détermination de l'angle du logarithme complexe est $[0;2\pi [$ , c.-à-d. si $\ln z=|z|+\mathrm {i} \,\theta$ avec $\theta \in [0;2\pi [$

[1] (en) Eric W. Weisstein, « Osborn's Rule », sur MathWorld.

[2] La norme ISO 31-11 recommande la notation « arsinh » pour cette fonction.

[3] La norme ISO 31-11 recommande la notation « arcosh » pour cette fonction.

[4] La norme ISO 31-11 recommande la notation « artanh » pour cette fonction.

[5] La norme ISO 31-11 recommande la notation « arcoth » pour cette fonction.

[7] $\operatorname {arcosh} \left(\mathrm {i} x\right)$ et $\operatorname {arsinh} x$ sur wolframalpha.com. La courbe correspond à $\operatorname {arcosh} (\mathrm {i} x)=\operatorname {sgn} x\cdot \left(\operatorname {arsinh} x+\mathrm {i} {\tfrac {\pi }{2}}\right)$ .

[8] $\operatorname {arsech} \left(\mathrm {i} x\right)$ et $\operatorname {arcsch} x$ sur wolframalpha.com. La courbe correspond à $\operatorname {arsech} (\mathrm {i} x)=\operatorname {sgn} x\cdot \left(\operatorname {arcsch} x-\mathrm {i} {\tfrac {\pi }{2}}\right)$ .

[1]

[2]

[3]

[4]

[5]

[Note 1]

[6]

[7]

v · m Fonctions mathématiques usuelles
Fonction algébrique rationnelle	Fonction polynomiale Fonction fractionnaire
Fonction algébrique irrationnelle	Fonction puissance / Fonction racine
Fonction transcendante	Fonction logarithmique / Fonction exponentielle de base a Fonction logarithme naturel / Fonction exponentielle Fonction circulaire / Fonction circulaire réciproque Fonction hyperbolique / Fonction hyperbolique réciproque Fonction elliptique / Fonction intégrale elliptique