درخت بازی - ویکی‌پدیا، دانشنامهٔ آزاد

درخت بازی :

که فرم گسترده هم خوانده می‌شود، نمایشی گرافیکی از یک بازی مرحله‌ای است که اطلاعاتی در مورد بازیکنان، نتایج نهایی، روش‌ها و مرتبهٔ حرکات فراهم می‌کند. درخت بازی تشکیل شده‌است از تعدادی رأس که نقاطی هستند که بازیکنان می‌توانند بر آن‌ها اقدام کنند، و این گره‌ها توسط یال، که نشان دهندهٔ اقداماتی است که ممکن است بر آن گره انجام شود، به هم متصل می‌شوند. اولین گره (یا ریشه) اولین تصمیمی که می‌بایست گرفته شود را نشان می‌دهد. هر مجموعه‌ای از یال‌ها از اولین گره به سرتاسر درخت، در آخر به گره‌ای نهایی می‌رسد، که نمایندهٔ انتهای بازی است. هر گرهٔ نهایی با نتیجه نهایی گرفته شده توسط هر بازیکن بر چسب گذاری می‌شود اگر بازی در آن گره پایان یابد.

استفاده از درخت برای نمایش فضای مسئله برای بازی‌ها اغلب مناسب است. گره ریشه شامل حالت شروع بازی می‌باشد. برای هر گره شامل وضعیت جاری، باید تصمیمی برای انتخاب بهترین حرکت بعدی اتخاذ شود. هر حرکت قانونی توسط یک شاخه از درخت نشان داده می‌شود. با استفاده از یک تابع ارزیابی، یک وضعیت از بازی ارزش گذاری می‌شود. گره‌های برگ، وضعیت‌های نهائی بازی را نشان می‌دهند که در اینجا می‌تواند یکی از مقادیر برد، مساوی یا باخت باشد.

مثال[ویرایش]

در بعضی بازی‌ها، برد یک طرف برابر با باخت طرف دیگر است، بازی‌هایی مانند: ایکس او و شطرنج. برای این نوع بازی‌ها، می‌توان درخت بازی طراحی کرد. مثالی از درخت بازی اکس او:

این شکل قسمتی از بازی ایکس او است. هر گره یک موقعیت از بازی را نشان می‌دهد، و بچه‌های هر گره، حرکات مجاز در آن موقعیت هستند. برای علامت گذاری هر موقعیت، به وضعی که برای بازیکن ۱ مطلوب است عددی مثبت اختصاص می‌دهیم (هر چه مثبت تر، مطلوب تر). به همین شکل، به وضعی که برای بازیکن ۲ مطلوب است عددی منفی اختصاص می‌دهیم (هر چه منفی تر، مطلوب تر). در این مثال، بازیکن شماره ۱، ‘X‘ و بازیکن شماره ۲، ‘O‘ است و تنها سه علامتی که داریم، ۱+ برای برد ‘X‘و ۱- برای برد ‘O‘، و ۰ برای تساوی است. توجه کنید که در اینجا علامت‌های آبی تنها با توجه به همان موقعیت به دست آمده‌اند. برای حساب کردن بقیه موقعیت‌ها، می‌بایست حرکاتی را پیش‌بینی کنیم که با استفاده از الگوریتم زیر به دست می‌آید.

تابع ارزیابی[ویرایش]

به منظور ارزیابی میزان خوب بودن یک گره، تابع ارزیابی استفاده می‌شود. (تابع هیوریستیک)
با استفاده از قانون مجموع صفر (Zero-Sum) می‌توان از یک تابع برای هر دو بازیکن به منظور ارزیابی موقعیت بازی بهره برد:

• برای من خوب و برای حریف بد است. n موقعیت F(n)> ۰
• برای من بد و برای حریف خوب است. n موقعیت F(n) <۰
• یک وضعیت خنثی است. n موقعیت F(n) = ۰
• برد من F(n)>> ۰
• برد حریف F(n) <<۰

قانون MiniMax[ویرایش]

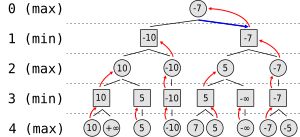
هدف از جستجو در درخت بازی، تعیین حرکتی (نه یک راه حل) برای بازیکن Max بطوری‌که امتیاز او را (بدون توجه به حرکات Min) ماکزیمم کند.

• پیچیدگی زمانی: (O(b^m (چرا که شبیه جستجوی عمقی کامل می‌باشد)
• پیچیدگی فضایی: از مرتبه خطی ((O(m یا (O(bm)

بازیکن Max همواره فرض می‌کند که بازیکن Min حرکتی را انجام می‌دهد که امتیازش را ماکزیمم کند و امتیاز Max را مینیمم کند.

امتیاز هر گره از طریق امتیاز فرزندانش مشخص می‌شود:

• مقدار گره Max برابر ماکزیمم مقدار فرزندانش است.
• مقدار گره Min برابر مینیمم مقدار فرزندانش است.

الگوریتم MiniMax[ویرایش]

حال که راهی برای نمایش بازی‌های خود داریم، چگونه می‌توانیم بهینه‌ترین حرکت را به دست آوریم؟ فرض می‌کنیم حریف ما هوشمند است، یعنی می‌تواند مانند ما حرکات را محاسبه کند و با انتخاب بهینه‌ترین حرکت، بازی خوبی ارائه دهد. یک الگوریتم برای محاسبه بهترین حرکت، الگوریتم minimax است:

minimax(player,board):     if game over in current board position:         return winner     children = all legal moves for player from this board     if max turn:         return maximal score of calling minimax on all the children     else min turn:         return minimal score of calling minimax on all the children 

1. گره شروع بازی را با برچسب Max ایجاد کن.
2. گره‌های سطوح بعدی را تا یک حد معین بسط بده.
3. تابع ارزیابی را به ازای هر گره برگ محاسبه کن.
4. برای گره‌های غیر برگ تا رسیدن به گره ریشه، با استفاده از قانون Minimax یک مقدار انتساب بده:
   1. مقدار گره Max برابر ماکزیمم مقدار فرزندانش است.
   2. مقدار گره Min برابر مینیمم مقدار فرزندانش است.
5. حرکتی را از گره جاری انتخاب کن که به بهترین گره برگ با ماکزیمم مقدار برسد.

اگر بازی در موقعیتی خاص تمام شود، دیگر چیزی برای محاسبه نیست و minimax علامت بازی را برمی‌گرداند. در غیر این صورت، minimax به تمام بچه‌های ممکن سر می‌زند، و (با بازگشتی خواندن خود)، هر حرکت ممکن را می‌سنجد و بعد از آن، بهترین حرکت را انتخاب می‌کند.

زمان الگوریتم[ویرایش]

چقدر این الگوریتم طول می‌کشد؟ برای بازی ساده‌ای مانند ایکس او، این زمان زیاد نیست – زیرا جستجوی تمام موقعیت‌های ممکن، امکان‌پذیر است. برای بازی‌های مانند شطرنج، زمان اجرا بسیار زیاد است. در حقیقت، برای اینکه تمام بازی‌ها را به‌طور کامل جستجو کنیم، ابتدا می‌بایست سفری بین ستاره‌ای تدارک ببینیم، زیرا پیش از پایان تحلیل یک حرکت، خورشید نابود شده و زمین دیگر وجود نخواهد داشت؛ بنابراین، تمام بازی‌های کامپیوتری تا تعدادی حرکت بعدی را جستجو می‌کنند، ولی نه تا پایان آن را. البته، برنامه می‌بایست تعیین کند که وضعیتی خاص برای بازیکنی خاص، خوب است یا بد. برای تحقق این امر، از تابع ارزیابی استفاده می‌کنیم. این تابع کلیدی برای بازی‌های قدرتمند کامپیوتری است.

بهینه‌سازی الگوریتم[ویرایش]

یک عمل بهینه‌سازی برای الگوریتم بالا وجود دارد که به ما این امکان را می‌دهد که حداکثر عمق جستجو را افزایش دهیم. برای فهم این ایده به این شرح توجه کنید: نوبت حرکت ماست و حرکتی (حرکت الف) را محاسبه کرده‌ایم که بیش‌ترین سودمندی را برایمان داشته‌است. اکنون در حال تحلیل حرکت دوم هستیم (حرکت ب)، و می‌بینیم حریف می‌تواند در اولین پاسخ خود، موقعیتی خنثی به وجود آورد! دلیلی برای آزمایش حرکت ب نیست. در اینجا، می‌دانیم بهترین کار در صورتی که حرکت ب را انجام داده باشیم، رسیدن به موقعیتی خنثی است، در حالی که قبل از آن حرکت الف را داشته‌ایم که خود تضمین گر موقعیتی بهتر است.

الگوریتم MiniMax بازی‌های چند نفره[ویرایش]

در بازی دو نفره دو بازیکن وجود داشت و دو مقدار تولید شده توسط تابع سودمندی که با توجه متضاد بودن این نتایج توانستیم آن‌ها را به یک مقدار در هر نوبت تبدیل کنیم.

استفاده از یک بردار برای نمایش وضعیت بازی به جای یک مقدار در بازی چند نفره تابع سودمندی مقادیر مختلفی را در این بردار به ازای هر برگ تولید می‌کند که هر یک از این مقادیر از دید بازیکن خاصی می‌باشد.

بازیکنان به‌طور رسمی یا غیررسمی با همدیگر در پیشبرد بازی همکاری می‌کنند.

شبه کد[ویرایش]

نمونه‌ای از یک شبه کد برای الگوریتم کمینه بیشینه:

function integer minimax(node, depth):     if node is a terminal node or depth == 0:         return the heuristic value of node     α = -∞     for child in node:                       # evaluation is identical for both players         α = max(α, -minimax(child, depth-1))     return α 

بهینه‌سازی[ویرایش]

در جستجوی Minimax تعداد گره‌های درخت جستجو به صورت نمائی افزایش می‌یابد.

برای حل این مشکل، راه حل پیشنهادی عدم بسط گره‌هایی است که مقدار آن‌ها تأثیری در تصمیم نهائی ندارد.

برای این منظور، کارایی الگوریتم Minimax را می‌توان با استفاده از هرس آلفا بتا افزایش داد.

الگوریتم آلفا بتا[ویرایش]

اکنون ما از دو مقدار آلفا و بتا برای تحلیل هر گره استفاده می‌کنیم، و این الگوریتم را هرس آلفا بتا می‌نامیم. آلفا ارزش بهترین حرکتی از ماست که محاسبه کرده‌ایم و بتا نیز ارزش بهترین حرکت برای حریف است که آن را خود محاسبه کرده‌ایم. هر زمان که آلفا>=بتا بود، بهترین حرکت حریف موقعیتی بدتر از بهترین حرکت ما ایجاد می‌کند، بنابراین نیازی به ارزیابی این حرکت نیست.

alpha-beta(player, board, alpha, beta):     if game over in current board position:         return winner     children = all legal moves for player from this board     if max turn:         for each child:             score = alpha-beta(other player,child,alpha,beta)             if score> alpha then alpha = score # we have found a better best move             if alpha>= beta then return alpha # cut off         return alpha # this is our best move     else min turn:         for each child:             score = alpha-beta(other player,child,alpha,beta)             if score <beta then beta = score # opponent has found a better worse move             if alpha>= beta then return beta # cut off     return beta # this is the opponent's best move 

این الگوریتم مقداری مشابه با minimax اما در زمانی سریع تر برمی‌گرداند.

پیچیدگی درخت بازی[ویرایش]

بازی‌هایی که گراف بزرگتری دارند دارای پیچیدگی بیشتری هستند و در نظریهٔ بازی‌ها سخت‌تر می‌باشند. مثلاً شطرنج نمونه‌ای از پیچیده‌ترین بازی‌ها با پیچیده‌ترین درخت بازی است.

در بسیاری از بازی‌ها تعداد حرکات ممکن، محدود است. برای مثال، در بازی ایکس او، بازیکنان با قرار دادن علامت X یا O بر صفحه بازی، نه موقعیت می‌توانند ایجاد کنند. بعد از قرار دادن یکی از این علامات، بازی با یک حرکت پیش رفته‌است.

درخت بازی ایکس او با نه شاخه آغاز می‌شود، زیرا بازیکن اول از بین نه خانه خالی می‌تواند یکی را انتخاب کند. با انتخاب هر یک از این نه خانه، بازیکن دوم می‌تواند در یکی از هشت خانهٔ باقی‌مانده علامت زند، بنابراین هر یک از این نه گره هشت شاخه دارند. با ادامهٔ این کار می‌توان درختی با ۳۶۲٬۸۸۰ = !۹ برگ ساخت، که برخی متعلق به برد بازیکن اول، و برخی متعلق به برد بازیکن دوم و بقیه مربوط به تساوی آن دوست.

ایکس او می‌تواند در پنج مرحله به پایان رسد، در صورتی که بازیکن اول تمام علامت‌ها را در یک ردیف بگذارد. به همین دلیل درخت بازی شامل شاخه‌هایی است که در مکان‌هایی بسیار کوتاه‌تر از عمق کامل آن بریده شده‌اند.

برای یافتن بهترین حرکت ممکن از الگوریتم minimax استفاده می‌شود.

شش میلیون حالت ممکن ایکس او برای به خاطر سپردن بازیکنان بسیار زیاد است، اما برای کامپیوترهای مدرن ناچیز می‌باشد. به همین دلیل این بازی با توجه به استانداردهای نظریه بازی، «سخت» در نظر گرفته نمی‌شود. بسیاری از بازی‌های جالب مانند شطرنج، دارای درخت‌های بازی ای هستند که تعداد حالات ممکن آن‌ها بسیار بیشتر از تعداد کل اتم‌ها در جهان است. این نوع بازی‌ها در ریاضی «سخت» خوانده می‌شوند، به این دلیل که، راهی برای حفظ تمامی حالات ممکن شطرنج نیست.

راه حل عمومی این نوع بازی‌ها، ساخت قسمتی از درخت است که بیانگر وضعیت کنونی می‌باشد. برای مثال ممکن است یک برنامه بازی شطرنج، از قالب کنونی صفحه، درختی با یک میلیون نتیجه ممکن بسازد، و الگوریتم آلفا بتا را به این قسمت از درخت اعمال کند. البته ممکن است سیستم، حرکتی را انتخاب کند که تمام نتایج حاصل در مرحلهٔ بعد منجر به باخت شود. این موضوع به تأثیر افقی (به انگلیسی: horizon effect) معروف است که تمام تغییرات مهم در جایی خارج از عمق درختی که جستجو شده‌است اتفاق افتد. به همین دلیل بسیاری از برنامه‌های شطرنج بزرگترین درخت ممکن را (با توجه به میزان حافظه و زمان) می‌سازند.

سرعت کامپیوترهای مدرن این مشکل را تا حدی رفع کرده‌است، حتی برنامه‌های شطرنج غیر نخبه می‌توانند در برابر همه به جز بهترین بازیکنان انسانی پیروز شوند.

تعداد موقعیت‌های قانونی و پیچیدگی درخت بازی برای بعضی بازی‌ها

ایکس او – ۳٫۶*۱۰^۶ موقعیت

شطرنج – ۱۰^۵۰ موقعیت – ۱۰^۵۸ پیچیدگی

تخمین پیچیدگی درخت بازی شطرنج[ویرایش]

عدد شانون (۱۰ به توان ۱۲۰) تخمین پیچیدگی درخت بازی شطرنج است.

این عدد اولین بار به وسیله کلود شانون پدر تئوری اطلاعات محاسبه شد. بر طبق نظر وی، به‌طور متوسط در هر بازی ۴۰ حرکت انجام می‌شود و هر بازیکن یک حرکت را بین۳۰ حرکت انتخاب می‌نماید. (اما در واقع ممکن است برخی حرکات انتخابی در حد صفر باشد مثلاً در موارد پات یا کیش و مات یا تا ۲۱۸ حرکت افزایش یابد).

بنابراین ۳۰*۳۰ به توان ۴۰ یا به عبارتی ۹۰۰ به توان ۴۰ بازی شطرنج ممکن است. این تعداد در حدود ۱۰ به توان ۱۲۰ است. پیچیدگی درخت بازی شطرنج اکنون در حدود ۱۰به توان ۱۲۳ (تعداد پوزیسیون‌های قانونی در بازی شطرنج بین ۱۰ به توان ۴۳ و ۱۰ به توان ۵۰) تخمین زده می‌شود. به عنوان مقایسه، تعداد اتم‌ها در جهان بین ۱۰*۴ به توان ۷۵ و۱۰*۶ به توان ۷۹ تخمین زده می‌شود.

منابع[ویرایش]