دایره - ویکی‌پدیا، دانشنامهٔ آزاد

دایره
یک دایره   محیط C   قطر D   شعاع R   مرکز O
نوع	مقطع مخروطی
گروه تقارن	O(2)
مساحت	πR2

هندسه
تصویر کره بر روی صفحه
خطوط کلی تاریخ هندسه
شاخه‌ها اقلیدسی نااقلیدسی بیضوی کروی هذلولوی غیر-ارشمیدسی تصویری آفین سینتتیک تحلیلی جبری حسابی سیاله‌ای دیفرانسیل ریمانی سیمپلکتیک گسسته مختلط متناهی گسسته دیجیتال محدب محاسباتی فراکتال وقوع
مفاهیم بعد ساخت با خط‌کش و پرگار زاویه منحنی قطر تعامد در جبر خطی (تعامد هندسی) توازی رأس هم‌نهشتی تشابه تقارن
صفر بعدی نقطه
فضای یک بعدی خط مستقیم پاره‌خط خط مستقیم طول
فضای دوبعدی صفحه مساحت چندضلعی مثلث ارتفاع (مثلث) وتر قضیه فیثاغورس متوازی‌الاضلاع مربع مستطیل لوزی Rhomboid چهارضلعی ذوزنقه کایت دایره قطر محیط منحنی مساحت دایره
فضای سه‌بعدی حجم مکعب مکعب مستطیل استوانه هرم (هندسه) کره (هندسه)
چهاربعدی / سایر ابعاد تسرکت ابرکره
فهرست هندسه‌دانان
براساس نام آیدا آریابهاتا احمس ابن هیثم آپولونیوس ارشمیدس مایکل عطیه Baudhayana یانوش بویایی برهماگوپتا الی کارتان هارولد اسکات مک‌دونالد کاکسیتر رنه دکارت اقلیدس لئونارد اویلر کارل فریدریش گاوس میخائیل لئونیوویچ گروموف دیوید هیلبرت Jyeṣṭhadeva کاتیایانا خیام فلیکس کلاین نیکلای لوباچفسکی Manava هرمان مینکوفسکی Minggatu بلز پاسکال فیثاغورس Parameshvara آنری پوانکاره برنهارت ریمان Sakabe ابوسعید سجزی خواجه نصیرالدین طوسی اسوالد وبلن Virasena Yang Hui al-Yasamin چانگ هنگ فهرست هندسه‌دانان
براساس دوره گاه‌شماری دوران مشترک احمس Baudhayana Manava فیثاغورس اقلیدس ارشمیدس آپولونیوس 1–1400s چانگ هنگ کاتیایانا آریابهاتا برهماگوپتا Virasena ابن هیثم ابوسعید سجزی خیام al-Yasamin خواجه نصیرالدین طوسی Yang Hui Parameshvara 1400s–1700s Jyeṣṭhadeva رنه دکارت بلز پاسکال Minggatu لئونارد اویلر Sakabe Aida 1700s–1900s کارل فریدریش گاوس نیکلای لوباچفسکی یانوش بویایی برنهارت ریمان فلیکس کلاین آنری پوانکاره دیوید هیلبرت هرمان مینکوفسکی الی کارتان اسوالد وبلن هارولد اسکات مک‌دونالد کاکسیتر روزگار کنونی مایکل عطیه میخائیل لئونیوویچ گروموف
ن ب و

از سلسله مقالاتی دربارهٔ مقاطع مخروطی
سهمی
معادله	${\displaystyle y^{2}=4ax\,}$
گریز از مرکز (${\displaystyle e}$)	${\displaystyle 1\,}$
نیم‌راست‌وتر کانونی (${\displaystyle l}$)	${\displaystyle 2a\,}$
هذلولی
معادله	${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$
گریز از مرکز (${\displaystyle e}$)	${\displaystyle {\sqrt {1+{\frac {b^{2}}{a^{2}}}}}}$
نیم‌راست‌وتر کانونی (${\displaystyle l}$)	${\displaystyle {\frac {b^{2}}{a}}}$
بیضی
معادله	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$
گریز از مرکز (${\displaystyle e}$)	${\displaystyle {\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}$
نیم‌راست‌وتر کانونی (${\displaystyle l}$)	${\displaystyle {\frac {b^{2}}{a}}}$
دایره (حالت خاص بیضی)
معادله	${\displaystyle x^{2}+y^{2}=a^{2}\,}$
گریز از مرکز (${\displaystyle e}$)	${\displaystyle 0}$
نیم‌راست‌وتر کانونی (${\displaystyle l}$)	${\displaystyle a}$
• • •
ن ب و

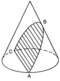
در هندسه، دایره یک منحنی مسطح و بسته و شامل نقاطی از صفحه است که فاصله‌شان از نقطهٔ ثابتی واقع در آن صفحه مقداری ثابت باشد. نقطهٔ ثابت، مرکز دایره و مقدار ثابت، اندازهٔ شعاع دایره نامیده می‌شود. همچنین دایره را می‌توان یک بیضی دانست که کانون‌های آن بر همدیگر منطبقند (برون‌مرکزی آن صفر است)؛ ازین‌رو دایره یکی از مقاطع مخروطی است. مقطع مخروطی منحنی‌ای است که در محل تقاطع یک صفحه با یک مخروط پدیدار می‌شود، و هنگامی که صفحه با مقطع مخروط موازی باشد منحنی حاصل دایره خواهد بود. دایره را همچنین می‌توان به عنوان چندضلعی متساوی‌الاضلاعی تعریف کرد که تعداد اضلاع آن به بی‌نهایت میل می‌کند.

دایره مجموعهٔ نقاط صفحه را به سه گروه تقسیم (اِفراز) می‌کند: داخل دایره (یا قرص)، روی دایره (یا محیط)، و بیرون دایره. نسبت محیط دایره به قطر آن (بیشترین فاصلهٔ بین دو نقطه روی محیط) همیشه ثابت است و عددِ پی ${\displaystyle (\pi )}$ نامیده می‌شود. محاسبهٔ عدد پی سابقه‌ای طولانی در تاریخ بشر دارد. ارشمیدس روشی با استفاده از چهارضلعی‌های محاطی و محیطی برای محاسبهٔ عدد پی ابداع کرد. آپولونیوس و غیاث‌الدین جمشید کاشانی هم عدد پی را با دقتی بالا محاسبه کردند. همچنین مساحت دایره برابر است با حاصلضربِ مربعِ شعاع دایره در عدد پی. دایره حداکثر مساحت ممکن برای مقدار معین محیط و حداقل محیط ممکن برای مقدار معین مساحت را دارد.

فلاسفهٔ یونان باستان (به پیروی از فیثاغوری‌ها و افلاطون) معمولاً مدل زمین‌مرکزی را با مدلی مبنی بر کروی بودن زمین درمی‌آمیختند و بر این باور بودند که زمین کره‌ای است در مرکز جهان و افلاک در دایره‌هایی به دور زمین در گردشند. بطلمیوس با ابداع دایره‌هایی به عنوان فلک تدویر و فلک حامل نظامی ارائه داد که ساختار هستی را بر اساس دایره توجیه کند. کوپرنیک هم با ارائهٔ نظریهٔ خورشیدمرکزی‌اش ساختار جهان را متشکل از دایره‌هایی به گرد خورشید دانست. در نهایت کپلر اعلام کرد که مسیر گردش سیارات به شکل بیضی و نه دایره است و نیوتن شرایطی را مشخص کرد که تحت آن مسیر حرکت دایره‌ای به یکی دیگر از مقاطع مخروطی بدل می‌شود.

دایره کامل‌ترین شکل هندسی دانسته می‌شود و در فناوری، هنر، دین، و فرهنگ اهمیتی عمده داشته‌است. پرگار (که ابزاری برای کشیدن دایره بر اساس تعریف آن با مرکز و شعاع [تعریف اقلیدسی] است) و خط‌کش، تنها ابزار مجاز در هندسه اقلیدسی‌اند، تا جایی که هندسهٔ اقلیدسی گاه «هندسهٔ خط‌کش و پرگار» خوانده شده‌است. تربیع دایره، تثلیث زاویه، و تضعیف مکعب سه مسئلهٔ دشوار و مهمی بودند که در طول تاریخ هندسه‌دانان را درگیر خود کردند. در قرن نوزدهم پیر ونزل و فردیناند فون لیندمن ثابت کردند که این مسائل غیرممکنند.

تاریخچه[ویرایش]

تاریخچهٔ مطالعهٔ دایره به پیش از آغاز تاریخ بازمی‌گردد؛ چنان‌که اختراع چرخ در هزارهٔ چهارم پیش از میلاد در میانرودان نشان از کشف ویژگی‌های بنیادی دایره دارد.^[۱] در مصر نیز احمس، نویسندهٔ پاپیروس ریاضی ریند، قانونی برای محاسبهٔ مساحت دایره به دست می‌دهد که با ${\displaystyle \pi ={\tfrac {256}{81}}\approx 3.16}$ مطابق است.^[۲] در کتیبه‌ای بابلی متعلق به ۱۹۰۰–۱۶۰۰ پ.م. هم رابطهٔ بین مساحت و پیرامون دایره بررسی و عدد پی به‌شکلی ضمنی ${\displaystyle \pi ={\tfrac {25}{8}}=3.125}$ تعریف شده‌است.^[۳]

تاریخ باستان[ویرایش]

نخستین قضایای مربوط به دایره دو قضیه از چهار قضیهٔ منسوب به تالس (ح. ۶۵۰ پ. م) هستند. او ثابت کرد که قطر دایره آن را به دو کمان مساوی تقسیم می‌کند و زاویهٔ محاطی‌ای که دایره را در دو سرِ یک قطرش قطع کند قائمه است.^[۴]

فیثاغوری‌ها باور داشتند که زمین کره‌ای است در مرکز هستی و ماه و خورشید و سیاره‌ها در دایره‌هایی هم‌مرکز روی یک صفحهٔ چرخ‌مانند به‌دور زمین در گردشند.^[۵] این نظریهٔ زمین‌مرکزی، باور غالب یونانیان باستان بود. بااین‌همه آریستارخوس ساموسی (ح. ۳۱۰ — ح. ۲۳۰ پ. م) نظریهٔ خورشیدمرکزی را مطرح کرد که در آن خورشید ثابت است و زمین در دایره‌ای به مرکزیت خورشید در حرکت.^[۶] همچنین فیلسوف یونانی افلاطون (۴۲۸/۴۲۷ — ۳۴۸/۳۴۷ پ. م) باور داشت که زمین کره‌ای بی‌نقص است و همهٔ حرکت‌های سماواتی در دایره‌هایی کامل و با سرعت یکسان به گرد آن صورت می‌گیرد.^[۷] این باور افلاطون به اصلی جزم‌اندیشانه در آکادمی افلاطون و بعدها در میان ستاره‌شناسان یونان باستان بدل شد.^[۸]

یکی از مسائل هندسی که یونانیان به‌شدت با آن درگیر بودند مسئلهٔ یافتن مربعی با مساحت مساوی دایره (اصطلاحاً تربیع دایره) بود. آناکساگوراس (ح. ۴۵۰ پ. م) نخستین ریاضی‌دان شناخته‌شده‌ای است که این مسئله را مطالعه کرده‌است.^[۹] بقراط خیوسی (۴۷۰ — ۴۱۰ پ. م) در تلاش برای حل تربیع دایره توانست ثابت کند که مساحت هلال کوچکتر ایجاد شده از برخورد دو دایره، برابر با مساحت مثلث قائم‌الزاویهٔ متساوی‌الساقینی است که وترش برابر وتر دایرهٔ کوچکتر و اضلاعش برابر شعاع دایرهٔ بزرگتر است. هلال بقراط نخستین منحنی‌ای بود که مساحت دقیق آن از طریق ریاضی محاسبه شد.^[۱۰] آریستوفان (ح. ۴۴۶ – ۳۸۶ پ. م) در نمایشنامهٔ پرنده‌ها «تربیع‌کنندگان دایره‌ها» را به سخره می‌گیرد.^[۱۱] دیگر مسائل بزرگی که ریاضی‌دانان یونانی را درگیر خود کرده بود تثلیث زاویه (تقسیم زاویه به سه قسمت مساوی) و تضعیف مکعب (دو برابر کردن حجم مکعب) با استفاده از پرگار و خط‌کش بود.

کتاب سوم اصول اقلیدس (ح. ۳۶۵ — ۲۷۵ پ. م) نیز تماماً به ویژگی‌های دایره و مسائل مربوط به محیط و محاط کردن آن نسبت به چندضلعی‌ها اختصاص دارد.^[۱۲] همچنین سومین اصل از اصول موضوعه اقلیدس بیان می‌دارد که «برای هر پاره خط دلخواه می‌توان دایره‌ای به شعاع آن پاره خط و به مرکز یک سر آن رسم کرد.» ارشمیدس (۲۸۷ — ۲۱۲ پ. م) هم در اندازه‌های دایره برای اولین بار فرمول مساحت دایره را اثبات کرد^[۱۳] و با چندضلعی‌های منتظم محیطی و محاطی ۹۶ضلعی، عدد پی ${\displaystyle (\pi )}$ را به صورت ${\displaystyle {\tfrac {223}{71}}<\pi <{\tfrac {22}{7}}}$ (یعنی ۳٫۱۴۰۸ < ${\displaystyle \pi }$ < ۳٫۱۴۲۹) تعریف و محاسبه کرد؛ ازین‌رو عدد پی در برخی منابع «عدد ارشمیدس» نامیده شده‌است.

آپولونیوس (ح. ۲۴۰ پ. م) به‌شکل ضمنی نشان داد که معادلهٔ دوقطبی ${\displaystyle r=kr'}$ با تغییر ${\displaystyle k}$ نظامی از دایره‌های هم‌محور را می‌سازد.^[۱۴] او همچنین در اثر مهمش با عنوان مخروطات،^[الف] دایره را به عنوان حالت خاص بیضی و یکی از مقاطع مخروطی مطالعه، خط مماس بر منحنی (که بعدها موضوع اصلی حساب دیفرانسیل شد) را تعریف، و عدد پی را با دقتی بیشتر از ارشمیدس محاسبه کرد.^[۱۵] او همچنین مسئله‌های آپولونیوس را مطرح و حل کرد و تعریفی متفاوت از دایره (به عنوان مکان هندسی نقاطی که نسبت فواصلشان از دو نقطه ثابت است) ارائه کرد.

بطلمیوس (ح. ۱۰۰ — ۱۶۸ میلادی) با ترکیب آرای ستاره‌شناسان پیشین در المجسطی، نظام زمین‌مرکزی‌اش را به‌گونه‌ای تعریف می‌کند که تمام ساختار هستی بر اساس شکل دایره توجیه شود.^[۱۶] به گفتهٔ بطلمیوس زمین و «افلاک» (به ترتیب ماه، عطارد، زهره، خورشید، مریخ، مشتری، و زحل) کاملاً کروی‌اند و زمین در مرکز گیتی ثابت و مستحکم شده‌است. به باور او افلاک با سرعت یکنواخت بر دایره‌ای کوچک به نام فلک تدویر در حرکتند و مرکز هر فلک تدویر با سرعتی یکنواخت بر دایره‌ای بزرگ به نام فلک حامل به مرکزیت زمین حرکت می‌کند. همهٔ این‌ها در داخل منطقه‌البروج قرار دارند که کره‌ای است ثابت و ستارگان روی آن استقرار یافته‌اند.^[۱۷] مدل بطلمیوس از جهان هستی تا زمان کوپرنیک و تیکو براهه فصل‌الخطاب اخترشناسی باقی ماند.^[۱۸]

در روم باستان، «سولکوس پریمیجنیوس»^[ب] آیینی بود مبنی بر این‌که پیش از بنانهادن هر شهر، پیشوایان مذهبی با هدایت خیشی بسته به دو گاو به دور محوطهٔ آن شیاری به شکل دایره رسم می‌کردند و باور بر این بود که این عمل از شهر حفاظت خواهد کرد. در اساطیر رومی نیز رومولوس به دور شهر رم شیاری دایره‌ای می‌کِشد و برادرش رموس را به علت ورود به این دایره می‌کُشد.^[۱۹]

در امپراتوری اشکانی نیز پایتخت‌ها و شهرهای مهم به شکل دایره ساخته می‌شدند؛ از جملهٔ این شهرها می‌توان از نسا، شهر گور، صددروازه، هترا، و تیسفون پارتی یاد کرد. به گفتهٔ گیرشمن، «طرح این شهرها، عدم امنیت دائمی را که در ایران عهد پارتیان حکفرما بود، عدم ثبات سیاست خارجی و اغتشاشات داخلی را آشکار می‌سازد… طرح عمومی آن‌ها عبارت است از دایره‌ای که از اصول شهرسازی قدیم آسیای غربی اقتباس شده و نیز طرح اردوگاه‌های نظامی قدیم را که در قشون آشوری متداول بوده‌است به خاطر می‌آورد.»^[۲۰]

همچنین در چین باستان لیو هوی (متولد ح. ۲۲۵ میلادی در کائو وی) با محاط کردن چندضلعی در دایره عدد پی را محاسبه کرد. تسو چونگچی (۴۲۹ — ۵۰۰ میلادی) نیز در رسالهٔ شیوهٔ الحاق^[پ] مقدار عدد پی را مستقل از لیو هوی ولی به شیوه‌ای مشابه برابر ${\displaystyle \pi \approx {\tfrac {355}{113}}}$ محاسبه کرد.^[۲۱]

قرون وسطی[ویرایش]

همزمان با حکومت مأمون در خراسان (در قرن سوم هجری)، اخوان ثلاثهٔ بنوموسی دست به ترجمهٔ مخروطات آپولونیوس از یونانی به عربی زدند. بنوموسی فقط نسخه‌ای ناقص از مخروطات را در اختیار داشتند و مقاطع مخروطی در زمان ایشان به دست فراموشی سپرده شده بود، بنابراین در فهم متن دچار مشکل بودند. اندکی بعد، یکی از اخوان ثلاثه به نام حسن، نظریهٔ مقاطع استوانه‌ای را ابداع کرد که می‌توان آن را مقدمه‌ای ساده بر مقاطع مخروطی دانست. پس از درگذشت حسن، برادرش احمد در شام نسخه‌ای کامل‌تر از چهار فصل اول مخروطات را با شرح اوتوکیوس پیدا کرد و به کمک برادر دیگرش، محمد، و با استفاده از دو نسخهٔ موجود و نظریهٔ حسن، موفق شد نظریات آپولونیوس را دریابد. احمد و محمد ترجمهٔ مقالهٔ اول تا چهارم مخروطات را به هلال حمصی و مقالهٔ پنجم تا هفتم آن را به ثابت بن قره سپردند و خود بازنگری نهایی ترجمه را عهده‌دار شدند. ترجمهٔ برادران بنوموسی از مقالات پنجم تا هفتم مخروطات تنها نسخهٔ باقی ماندهٔ این اثر است.^[۲۲]

بنوموسی در باب مسئلهٔ تثلیث زاویه (تقسیم یک زاویه به سه قسمت مساوی با استفاده از پرگار) نیز راه حلی با استفاده از مقاطع مخروطی پیشنهاد کردند. ابوجعفر خازن خراسانی (؟ — ۳۶۰ ه‍.ق)، ابوسهل بیژن کوهی (؟ — ۴۰۵ ه‍.ق) و ابوسعید سجزی (ح. ۳۳۰ — ح. ۴۱۵ ه‍.ق) نیز راه‌حل‌هایی در مورد این قضیه ارائه کردند. ابوریحان بیرونی (۳۶۲ — ۴۴۲ ه‍.ق) هم ۱۲ مسئله طرح کرد و نشان داد با حل شدن هر کدام، مسئلهٔ تثلیث زاویه هم حل می‌شود.^[۲۳]

عبدالرحمن صوفی (۲۹۱ — ۳۷۶ ه‍. ق) به درخواست عضدالدولهٔ دیلمی (۳۲۴ — ۳۷۲ ه‍.ق) کتابی با عنوان رسالة فی عمل المتساویة الاضلاع کلها بفتحة واحدة نوشت و در آن ترسیم چندضلعی‌های منتظم را با خط‌کش و پرگاری با دهانهٔ ثابت مطالعه کرد.^[۲۴] ابوالوفا محمد بوزجانی (۳۲۸ — ۳۸۸ ه‍.ق) هم در کتاب فیما یحتاج الیه الصانع من الاعمال الهندسه^[ت] یا اعمال هندسی در مورد ترسیم اشکال هندسی با پرگاری با دهانهٔ ثابت بحث کرده‌است.^[۲۴]

غیاث‌الدین جمشید کاشانی (۷۵۸ — ۸۰۸ ه‍.ق) در الرِسالةُ المُحیطیة نسبت محیط دایره به قطر آن (عدد پی) را با ۱۶ رقم اعشار محاسبه کرد. کاشانی این محاسبات را به کمک دو ۳ × ۲^۲۸ضلعی انجام داد که یکی محاط در و دیگری محیط بر دایره بودند. او همچنین در مقدمهٔ مفتاح الحساب می‌نویسد که در رسالهٔ وتر و جیب، که امروز گمشده است، با استفاده از حل جبری معادلات درجهٔ سوم راه حلی برای تثلیث زاویه ارائه کرده بود.^[ث][۲۴]

رنسانس و قرون جدید[ویرایش]

در دههٔ ۱۵۴۰، کوپرنیک نظریه خورشیدمرکزی‌اش را ارائه کرد. در مدل خورشیدمرکزی کوپرنیک مسیر حرکت سیارات به دور خورشید به شکل دایره‌هایی به دور دایره (مشابه فلک‌های تدویر و فلک حامل در مدل بطلمیوسی) است. در مدل کوپرنیک:

عطارد در نهایت بر روی هفت دایره می‌چرخد، زهره بر پنج، زمین بر سه، و به دور آن ماه بر چهار، و در نهایت مریخ و مشتری و زحل هر کدام بر پنج؛ یعنی در کل ۳۴ دایره کافی است تا بتوان همهٔ ساختار گیتی و رقص سیارات را توصیف کرد.

— ^[۲۵]

کوپرنیک خود می‌دانست که پیچیدگی دایره‌هایی به دور دایره دقیقاً با داده‌های ریاضی نمی‌خواند، با این حال به باور او مدل خودش از مدل بطلمیوسی (که از ۴۰ دایره برای توصیف جهان هستی استفاده می‌کرد) ساده‌تر و دقیق‌تر بود.^[۲۶] کوپرنیک در ویرایش‌های بعدی مدلش و برای تطبیق با داده‌های موجود مجبور شد تعداد دایره‌ها را به ۴۸ افزایش دهد. به نوشتهٔ آرتور کستلر در خوابگردها، «وسواس و خیال‌پردازی کوپرنیک نسبت به دایره‌ها و کره‌ها باعث شد مدل او به جای نظام ساده و هماهنگی که می‌توانست باشد به کابوسی دردناک و سردرگم بدل شود.»^[۲۷]

در ۱۶۰۲ میلادی، کپلر در پی رفع نارسایی‌هایی مدل کوپرنیک و با بیان این نکته که هر دایره را با داشتن سه نقطه روی محیط آن می‌توان تعریف کرد و اینکه مکان مریخ در فصل‌های مختلف در صورت سه نقطه‌ای دایره قرار نمی‌گیرد، دایره بودن مدار سیارات را رد کرد.^[۲۸] او به این نتیجه رسید که مسیر حرکت سیارات به شکل تخم‌مرغ (خاگی) است و فواصل بین آنها بر اساس اجسام افلاطونی تعیین می‌شود. تیکو براهه (۱۵۴۶–۱۶۰۱ م) با تکیه بر مشاهدات ۳۵ ساله‌اش از حرکت مریخ،^[ج] نظریات کپلر را دربارهٔ شکل منظومهٔ شمسی رد کرد.^[۳۰] براهه خود در ۱۵۸۸ نظامی از جهان هستی ارائه کرده بود تا «مزیت‌های فیزیکی مدل بطلمیوسی را با مزیت‌های ریاضیاتی مدل کوپرنیکی» ترکیب کند. در نظام براهه‌ای زمین در مرکز جهان قرار دارد و ماه و خورشید در دایره‌هایی به دور آن می‌گردند، ولی مدار دیگر سیارات (عطارد، زهره، مریخ، مشتری، و زحل) دایره‌هایی است به دور خورشید. براهه همچنین کپلر را دعوت کرد که به رصدخانهٔ او در پراگ — که آن زمان پایتخت امپراتوری مقدس روم بود — برود. کپلر، در تلاش برای حل ناهماهنگی بین مدلش از هستی و مشاهدات براهه، به این کشف مهم نایل شد که سیارات در مداری بیضوی (برون‌مرکزی‌دار) و نه مدور به دور خورشید می‌گردند.^[۳۱] کپلر همچنین در کتاب هارمونی جهان (۱۶۱۸) مفهوم هارمونی و هم‌نهشتی را به صورت هندسی در ریاضیات، موسیقی، اختربینی، و اخترشناسی مطالعه می‌کند و فواصل مطبوع موسیقی را با شکل دایره متناظر می‌داند. برای مثل به باور کپلر علت اینکه فاصله‌هایی با نسبت ۳:۵ (فاصلهٔ ششم بزرگ در نظام کوک خالص) مطبوعند و فاصله‌هایی با نسبت ۳:۷ نامطبوع این است که پنج‌ضلعی منتظم را می‌توان را با خط‌کش و پرگار رسم کرد ولی هفت‌ضلعی منتظم را نمی‌توان.^[۳۲]

نیوتن (۱۶۴۲—۱۷۲۷) در اصول ریاضی فلسفه طبیعی از دایره با عنوان «مسیر»^[چ] یاد می‌کند. نیوتن، بیست سال پیش از نگارش اصول، حرکت دایره‌ای را (که در زمان تعادل کامل گرانش و مرکزگریزی روی می‌دهد) مطالعه و قوانین آن را کشف کرده بود. طبق محاسبات او، در صورت عدم تعادل کامل بین گرانش و مرکزگریزی، برون‌مرکزیِ مسیرِ حرکت از صفر بیشتر می‌شود و مدار به یکی دیگر از مقاطع مخروطی (بیضی، سهمی، یا هذلولی) بدل می‌گردد.^[۳۳] همچنین مبحث خط مماس بر منحنی، راهنمای هر دوی نیوتن و لایبنیتس در ابداع مستقل حساب دیفرانسیل و انتگرال (انتشار در ۱۶۸۴ میلادی) بود.^[۳۴] انتگرال‌گیری (یافتن مساحت زیر یک تابع) در واقع تعریف مدرن مسئلهٔ تربیع دایره (یافتن مستطیلی با مساحت مساوی دایره) است و نیوتن خود به جای لفظ «انتگرال‌گیری» (که از تعاریف لایبنیتس گرفته‌شده‌است) از عبارت «تربیع منحنی»^[ح] استفاده می‌کرد.

در تاریخ معاصر[ویرایش]

در سال ۱۷۸۶ کارل فریدریش گاوس ثابت کرد که هفده‌ضلعی منتظم را می‌توان با پرگار و خط‌کش ترسیم کرد. پنج سال بعد نیز شرایط قابل رسم بودن چندضلعی منتظم با پرگار و خط‌کش را تدوین کرد و نشان داد که بیشتر چندضلعی‌ها را نمی‌توان با خط‌کش و پرگار ترسیم کرد. گابریل لامه (۱۸۷۰–۱۷۹۵) با تعمیم معادلهٔ بیضی، دایره را به همراه مربع در ردهٔ ابربیضی‌ها یا «منحنی‌های لامه» دسته‌بندی کرد.^[۳۵] در ۱۸۳۷ نیز پیر ونزل با استفاده از نظریهٔ میدان ثابت کرد تثلیث زاویه (تقسیم یک زاویه به سه قسمت مساوی با استفاده از خط‌کش و پرگار) و تضعیف مکعب (ساخت مکعبی با دوبرابر حجم مکعب اولیه با استفاده از خط‌کش و پرگار) مسائلی غیر ممکنند. از همین رو آگوست دمورگان (۱۸۰۶ — ۱۸۷۱) در کتاب خلاصه‌ای از تناقض‌ها^[خ] «ابلهان تناقض‌کار» یعنی «تربیع‌کنان دایره»، «تثلیث‌کنان زاویه»، و «تضعیف‌کنان مکعب» را نقد می‌کند.^[۳۶] در ۱۸۸۰ جان ون با ترکیب دیاگرام اویلر و آرای جرج بول، نمودار ون را ابداع کرد که در آن مجموعه‌ها به صورت دایره‌های همپوشان تصویر می‌شوند. در ۱۸۸۲ فردیناند فون لیندمن نشان داد که پی عددی متعالی است، و بنابراین ثابت کرد که تربیع دایره (رسم مربعی با مساحت برابر دایره) مسئله‌ای غیرممکن است. پیت هاین (۱۹۰۵–۱۹۹۶) نیز ابرمعادلهٔ ابربیضی‌ها را به‌دست‌آورد و از آن‌ها در طراحی‌های خود استفاده کرد.^[۳۷]

کاربرد[ویرایش]

دایره کامل‌ترین شکل ریاضیاتی دانسته می‌شود و در تاریخ تمدن بشری اهمیتی عمده داشته‌است.^[۳۸] تقریباً همهٔ وسایل نقلیه بر اساس چرخش چرخ کار می‌کنند که وسیله‌ای دایره‌شکل است.^[۳۹] اغلب ابزار مکانیکی و الکترومکانیکی نیز برای انتقال توان از چرخ‌دنده بهره می‌برند که معمولاً به شکل دایره است.^[۴۰] مولدهای الکتریکی هم بر اساس چرخش دوّار هادی در میدانی مغناطیسی عمل می‌کنند. مثلث رولو (اشتراک سه دایره با شعاع مساوی که مرکز هر کدام در تقاطع دو تای دیگر واقع شده‌است) می‌تواند در داخل یک مربع بچرخد.^[۴۱] این ویژگی بنیاد سازوکار متهٔ واتز^[د] است.^[۴۲] روتور موتور وانکل نیز به شکل مثلث رولو است.

در دین‌ها و فرهنگ‌های مختلف، دایره نماد تکامل، بی‌نهایتی، و الوهیت است.^[۴۳] در دین هندو و آیین بودا، ماندالا یا دوایر کیهان‌نما طرح‌هایی پیچیده‌اند که رابطهٔ جهان اصغر^[ذ] و جهان اکبر^[ر] به تصویر می‌کشند. در اسلام، دایره نماد «جلال خداوندی» است^[۴۴] و در مسیحیت پرگار بیانگر «ابتکار آفرینش» از سوی خدای پدر است.^[۴۵] در عرفان یهودی هم درخت زندگی دیاگرامی با ده دایره به نام سفیروت است که هرکدام نماد صورتی از هستی‌اند.^[۴۶] پرگار و گونیا نماد اصلی انجمن برادری فراماسونری است و نشان ماسونی نقطه‌ای درون دایره نیز به عنوان نماد جهان هستی به کار می‌رود.^[۴۷] در علوم خفیه دایره شکلی بنیادی است و آیین کشیدن «دایره تعویذ» به دور فرد او را از ارواح خبیث و خطرهای روحانی محافظت می‌کند و برای تبدیل مکان به «حرم غصب‌ناکردنی» به کار می‌رود.^[۴۸] صوفی‌ها هم روی زمین دایره‌ای موسوم به «خط عزیمت» می‌کشیدند و درون آن نماز‌هایی با سوره سجده‌دار می‌خواندند.^[۴۴] در روان‌شناسی تحلیلی نیز یونگی‌ها دایره را نماد «خود» می‌دانند.^[۴۴] حلقه هم در فرهنگ‌های مختلف به‌عنوان نماد اتحاد، یگانگی، موقعیت اجتماعی، و اقتدار به‌کار می‌رود.^[۴۹]

از آغاز معماری در دوران نوسنگی، دایره به دلایل کاربردی و نمادین نقشی بنیادی در ساخت‌وساز بوده‌است. استون‌هنج، شناخته‌شده‌ترین اثر دوران نوسنگی، به شکل دایره است.^[۵۰] ردپای مسئلهٔ تربیع دایره را هم می‌توان در تاریخ معماری دید؛ چنان‌که محیط مقطع هرم بزرگ جیزه برابر است با محیط دایره‌ای به شعاع ارتفاع هرم.^[۵۱] همچنین مفهوم مرد ویترویوسی، که بنیان معماری غربی از دوران روم تا دوران مدرن بوده، بر اساس تربیع دایره شکل گرفته‌است.^[۵۲] به باور پال کلتر،^[ز] از آنجا که مربع نماد زمین است و دایره نماد تکامل و الوهیت، تربیع دایره نماد جهانی ایجاد تعادل بین دنیای دنی و عالی است.^[۵۳] به گفتهٔ هانری استیرلن هم عمدهٔ تلاش‌ها و نوآوری‌های معماران ایرانی بعد از دوران اشکانی معطوف به ایجاد ارتباط بین پلان مربعی ابنیه و مقطع دایره‌ای پایهٔ گنبد بوده‌است.^[۵۴] از دیگر الگوهای دایره‌ای در تاریخ معماری می‌توان به معابد گرد و روتونداها در معماری رومی، رمانسک و رنسانس، معابد آسمان و خانه‌های فوجیان تالو در چین، و پنجره‌ها در معماری گوتیک اشاره کرد. از آنجا که پرگار از ابزار اصلی سازندگان و معماران در طول تاریخ بوده‌است، اشکالی که می‌توان آن‌ها را با پرگار کشید (مانند چهارضلعی، پنج‌ضلعی، و شش‌ضلعی) در آثار معماری نقش عمده‌تری دارند و اشکالی که نمی‌توان با پرگار ترسیمشان کرد (مانند هفت‌ضلعی) نادرند.^[۵۵] در نقاشی‌های مذهبی، قدیسان غالباً با هالهٔ نوری دایره‌ای شکل به گرد سرشان به تصویر کشیده می‌شوند.^[۵۶] در تئوری موسیقی غربی، برای نمایش هندسی اعتدال مساوی دوازده‌نتی گام کروماتیک غالباً از دیاگرامی دایره‌شکل (از جمله دایره پنجم‌ها، که قدمت آن به فیثاغورث می‌رسد، و دایره کروماتیک) استفاده می‌شود.^[۵۷] در تئوری موسیقی قدیم ایران و کشورهای دیگر جهان اسلام هم نظریهٔ ادوار دستان‌بندی سازها (نحوهٔ کوک ساز و موقعیت پردههای آن) را با کمک مجموعه‌ای از دایره‌ها توصیف می‌کرده‌است.^[۵۸]

تعریف دایره[ویرایش]

تعریف اقلیدسی[ویرایش]

دایره مکان هندسی همهٔ نقاطی است که از یک نقطهٔ معین (موسوم به مرکز دایره) فاصله‌ای ثابت (موسوم به شعاع) داشته باشند؛ یعنی:^[۵۹]

${\displaystyle C(O,R)=O(R)=\{x:{\overline {Ox}}=R\}}$

این تعریف دایره معادل همان تعریفی است که اقلیدس در اصول ارائه می‌کند:

دایره شکلی مسطح است که در یک خط به نام محیط مظروف شده‌است، به‌شکلی که همهٔ خط‌های راستی که از یک نقطهٔ معین در داخل آن به محیط کشیده می‌شوند با یکدیگر مساویند.

— اصول اقلیدس، مقالهٔ ۱ گزارهٔ ۱۵^[۶۰]

و

نقطهٔ مذکور «مرکز دایره» نام دارد.

— اصول اقلیدس، مقالهٔ ۱ گزارهٔ ۱۶^[۶۱]

تعریف آپولونیوسی[ویرایش]

آپولونیوس نشان داد که دایره را می‌توان به عنوان مکان هندسی همهٔ نقاطی نشان داده که نسبت فواصلشان از دو نقطهٔ ثابت عددی است ثابت و برابر با نسبت فواصل دو نقطهٔ ثابت از دایره؛ یعنی:

${\displaystyle {\frac {|AP|}{|BP|}}={\frac {|AC|}{|BC|}}}$

این دو نقطه به «کانون» های دایره موسومند. می‌توان با عملیات‌های جبری ساده ثابت کرد که تعریف آپولونیوسی و اقلیدسی معادل یکدیگرند.

دایره به عنوان حالت خاص چندضلعی[ویرایش]

دایره را می‌توان چندضلعی منتظمی با شعاع محاطی^[ژ] ${\displaystyle r}$ و شعاع محیطی^[س] ${\displaystyle R}$ دانست که تعداد اضلاع آن به بی‌نهایت میل می‌کند. در هندسه، از دایره‌ای با این تعریف با عنوان‌های بی‌نهایت‌ضلعی و تک‌ضلعی یاد شده‌است.

با این تعریف، محیط دایره برابر است با:^[۶۲]

${\displaystyle {\begin{aligned}C=\lim _{n\to \infty }2rn\tan {({\tfrac {\pi }{n}})}=2\pi r\\=\lim _{n\to \infty }2Rn\sin {({\tfrac {\pi }{n}})}=2\pi R\end{aligned}}}$

و مساحت آن برابر است با:^[۶۳]

${\displaystyle {\begin{aligned}A=\lim _{n\to \infty }nr^{2}\tan {({\pi }{n})}=\pi r^{2}\\=\lim _{n\to \infty }{\tfrac {1}{2}}nR^{2}\sin {({\tfrac {2\pi }{n}})}=\pi R^{2}\end{aligned}}}$

که هر دو حدشان یکی است، چرا که با میل کردن ${\displaystyle n}$ به بی‌نهایت، ${\displaystyle r}$ و ${\displaystyle R}$ به یک پاره‌خط (شعاع دایره) میل می‌کنند.^[۶۴]

به عنوان مقطع مخروطی[ویرایش]

دایره «حالت خاص تبهگون»^[ش] از بیضی است که در آن نیم‌قطر بزرگ و نیم‌قطر کوچک مساوی‌اند (برون‌مرکزی آن صفر است). ازین رو دایره یکی از مقاطع مخروطی است، به این مفهوم که در محل برخورد مخروطی قائم و صفحه‌ای که با قاعدهٔ آن مخروط موازی باشد دایره پدید می‌آید.^[۶۵] در هندسه تصویری، اشتقاق دایره از مخروط معادل تصویر مرکزی مقطع مخروط روی صفحه‌ای است که با قاعدهٔ مخروط موازی است.^[۶۶]

ویژگی‌های دایره[ویرایش]

شعاع، قطر، و وتر[ویرایش]

پاره‌خطی که مرکز دایره را به یکی از نقاط روی محیط دایره وصل می‌کند شعاع نام دارد و می‌توان آن را «بردار شعاع» آن نقطه دانست.^[۶۷] شعاع معمولاً با حرف لاتین ${\displaystyle r}$^[ص] نشان داده می‌شود.

قطر دایره حداکثر فاصلهٔ بین دو نقطه روی محیط دایره است و اندازهٔ آن دو برابر شعاع دایره است. هر قطر دایره از مرکز دایره می‌گذرد و دایره را به دو کمان مساوی تقسیم می‌کند. این کمان‌ها نیم‌دایره نامیده می‌شوند. خود قطر هم توسط مرکز دایره به دو پاره‌خط مساوی تقسیم می‌شود.^[۶۸] قطر دایره معمولاً با حرف لاتین ${\displaystyle d}$^[ض] نشان داده می‌شود.

پاره‌خطی که دو نقطهٔ متمایز از یک دایره را به هم پیوند می‌دهد، وتر^[ط] یا زِه آن دایره نامیده می‌شود. هر وتری که از مرکز دایره بگذرد حداکثر اندازهٔ ممکن برای وتر یک دایره را دارد و همان قطر دایره است.^[۶۹]

خط مماس[ویرایش]

خط‌ها یا با دایره در دو نقطه برخورد می‌کنند، یا در یک نقطه، یا با دایره برخورد نمی‌کنند. هر خطی که با دایره تنها در یک نقطه برخورد کند (آن را در یک نقطه لمس کند) به خط مماس (یا خط تانژانت) بر دایره در آن نقطه موسوم است. خط‌هایی که دایره را در دو نقطه قطع می‌کنند هم خط سکانت نامیده می‌شوند^[۷۰] و خطوطی که با دایره برخورد نمی‌کنند «خط پاسان»^[ظ] نام دارند.

از هر نقطهٔ بیرون دایره، دو خط مماس بر آن دایره می‌توان رسم کرد. این دو مماس طول یکسانی دارند. همچنین اگر از نقطهٔ ${\displaystyle D}$ بیرون دایره‌ای به مرکزیت ${\displaystyle O}$ بتوان دو مماس بر نقاط ${\displaystyle A}$ و ${\displaystyle B}$ روی محیط دایره رسم کرد، زاویه‌های ${\displaystyle \angle BOA}$ و ${\displaystyle \angle BDA}$ مکملند.^[۷۱] شعاع دایره نیز در نقطهٔ تماس بر خط مماس عمود است${\displaystyle ({\overline {AC}}\perp {\overline {CD}})}$.^[۷۲]

زاویه مرکزی و زاویه محاطی[ویرایش]

زاویه‌ای که از برخورد دو شعاع یک دایره پدید می‌آید زاویهٔ مرکزی نام دارد. رأس زوایای مرکزی در مرکز دایره قرار دارد. هر زاویهٔ مرکزی از قرص دایره یک قطاع جدا می‌کند.^[۷۳] همچنین هر زاویهٔ مرکزی از محیط دایره یک کمان جدا می‌کند، که به آن کمان نظیر آن زاویهٔ مرکزی گفته می‌شود. طول کمان نظیر هر زاویهٔ مرکزی ${\displaystyle (L)}$ برابر حاصلضرب شعاع دایره ${\displaystyle (r)}$ در اندازهٔ آن زاویه مرکزی بر حسب رادیان ${\displaystyle (\theta )}$ است ${\displaystyle (L=r\theta )}$. اگر اندازهٔ زاویهٔ مرکزی ${\displaystyle (\alpha )}$ بر حسب درجه نوشته شود، طول کمان نظیر آن برابر است با ${\displaystyle L={\tfrac {\alpha \pi r}{180}}}$.

از برخورد دو خط سکانت روی محیط دایره زاویهٔ محاطی پدید می‌آید. رأس زوایای محاطی روی محیط دایره قرار دارد.^[۷۴] هر زاویهٔ محاطی یک کمان از دایره جدا می‌کند که به آن کمان نظیر آن زاویهٔ محاطی گفته می‌شود. اندازه کمان نظیر هر زاویهٔ محاطی در دایره نصف اندازهٔ زاویهٔ محاطی روبروی آن کمان است. حالت تبهگون زاویهٔ محاطی زمانی رخ می‌دهد که یکی از اضلاع زاویه بر دایره مماس باشد، و به زاویهٔ مماسی موسوم است.

زاویه مرکزی[ویرایش]

زاویه‌ای که راس آن مرکز دایره و دو ضلع آن شعاع‌های دایره می‌باشند.

نکته: اندازه زاویه مرکزی با اندازه کمان روبرو آن برابر است.

زاویه محاطی[ویرایش]

زاویه‌ای که راس آن روی محیط دایره و دو ضلع آن وترهایی از دایره می‌باشد.

نکته: اندازه زاویه محاطی برابر است با نصف کمان روبرو.

کمان، قطاع، و قطعه[ویرایش]

هر دو نقطه A و B روی محیط دایره آن را به دو کمان تقسیم می‌کنند. برحسب عرف، کمان کوچکتر روی دایره (کمانی که زاویهٔ مرکزی متناظر آن کمتر از ۱۸۰° باشد) با نقاط دو سر آن ${\displaystyle ({\widehat {AB}})}$ و کمان بزرگتر (کمانی که زاویهٔ مرکزی متناظر آن بیشتر از ۱۸۰° باشد) با نقاط دو سر آن و نقطه‌ای در میان آن دو ${\displaystyle ({\widehat {ACB}})}$ مشخص می‌گردد. کمانی که زاویهٔ مرکزی متناظر آن مساوی ۱۸۰° باشد نیم‌دایره نام دارد.^[۷۵] مجموع زوایای متناظر دو کمان حاصل از دو نقطه روی دایره همواره برابر ۳۶۰° است.

قطاع بخشی از قرص دایره است که با دو شعاع (یک زاویهٔ مرکزی) و یک کمان محدود شده‌است. قطعه دایره نیز بخشی از قطاع است که بین کمان و وتر بین دو سر شعاع‌های زاویهٔ مرکزی قرار دارد.

محیط[ویرایش]

اگر شعاع دایره ${\displaystyle r}$ و قطر آن ${\displaystyle d}$ باشد، محیط دایره برابر است با:^[۷۶]

${\displaystyle C=\pi d=2\pi r}$

این فرمول را می‌توان با استفاده از حسابان و فرمول طول قوس در مختصات قطبی اثبات کرد:

${\displaystyle C=\int _{0}^{2\pi }{\sqrt {r^{2}+({\frac {dr}{d\theta }})^{2}}}d\theta =\int _{0}^{2\pi }{r}d\theta =2\pi r}$

دایره حداقل محیط برای یک مقدار معین مساحت را دارد.^[۷۷] نسبت محیط به قطر دایره ${\displaystyle ({\tfrac {C}{d}})}$ با بزرگ و کوچک شدن آن ثابت می‌ماند. این نسبت با علامت ${\displaystyle \pi }$ (پی) نشان داده می‌شود و می‌توان ثابت کرد که عددی متعالی و تقریباً برابر ۳/۱۴۱۵۹ است.^[۷۸][۷۹]

مساحت[ویرایش]

هم چنان‌که ارشمیدس با استفاده از روش افنا ثابت کرد، مساحت دایره برابر است با حاصلضرب مساحت مربعی که ضلعش برابر شعاع دایره است در نسبت محیط دایره به قطر آن (که همیشه عدد ثابت است و با حرف ${\displaystyle \pi }$ نشان داده می‌شود). یعنی:

${\displaystyle \pi r^{2}}$ = ${\displaystyle (r\times r)\times ({\frac {C}{d}})}$ = مساحت

دایره حداکثر مساحت ممکن برای مقدار معین محیط را دارد.^[۸۰]

اثبات[ویرایش]

مساحت دایره بر اساس محیط و شعاع آن تعیین می‌شود. اگر یک دایرهٔ مفروض به چهار قطاع مساوی تقسیم شود:

و به صورت زیر کنار هم چیده شود:

مشاهده می‌شود که شکل حاصل نامتعارف است. اما اگر دایرهٔ مفروض به قطاع‌های بیشتری تقسیم شود و همین روند ادامه یابد، مشاهده می‌شود که شکل به دست آمده به متوازی‌الاضلاع نزدیک می‌شود. به عنوان نمونه در مرحله‌ای که دایره مفروض به هشت قطاع مساوی تقسیم می‌شود، حاصل شکل زیر خواهد بود (که به متوازی‌الاضلاع نزدیک تر است):

اگر فرض را بر این باشد که دایره به تعداد بی‌شمار قطاع مساوی مساوی تقسیم شده‌است، آن گاه شکل حاصل متوازی‌الاضلاعی خواهد بود که به مستطیل خیلی نزدیک است.^[۸۱] با دانستن اینکه مساحت این متوازی‌الاضلاع با دایرهٔ مفروض برابر است، با ضرب کردن ارتفاع متوازی‌الاضلاع (که همان شعاع دایره است) در ضلع بزرگ متوازی‌الاضلاع مساحت دایره به دست می‌آید. قابل توجه است که اضلاع بزرگ متوازی‌الاضلاع همان کمان‌های نظیر قطاع‌ها را تشکیل می‌دهند؛ پس می‌شود گفت که هر ضلع بزرگ متوازی‌الاضلاع برابر با نصف محیط دایرهٔ مفروض خواهد بود؛ یعنی اندازهٔ آن ${\displaystyle {\tfrac {C}{2}}={\tfrac {2\pi r}{2}}=\pi r}$ خواهد بود. اندازهٔ ضلع کوچک متوازی‌الاضلاع هم که ${\displaystyle r}$ (شعاع دایره) است، پس مساحت دایره ${\displaystyle A=r\times \pi r=\pi r^{2}}$ خواهد بود.^[۸۲]

این اثبات را می‌توان با استفاده از مختصات قطبی به شکل صوری زیر نوشت:^[۸۳]

${\displaystyle A=\int _{0}^{2\pi }{d\theta }\int _{0}^{r}rdr=(2\pi )({\frac {1}{2r^{2}}})=\pi r^{2}}$

اِفرازِ صفحه توسط دایره[ویرایش]

دایره صفحه را به سه بخش اِفراز می‌کند:

1. داخل دایره: مجموعه نقطه‌هایی مانند ${\displaystyle I}$، که فاصلهٔ آن‌ها از مرکز دایره، کمتر از شعاع دایره است. داخل دایره به قرص موسوم است.^[۸۴]
2. روی دایره: مجموعه نقطه‌هایی مانند ${\displaystyle M}$، که فاصلهٔ آن‌ها از مرکز دایره، برابر شعاع دایره است.
3. خارج دایره: مجموعهٔ نقطه‌هایی مانند ${\displaystyle E}$، که فاصلهٔ آن‌ها از مرکز دایره، از شعاع دایره بیشتر است.

اشتراک دایره‌ها[ویرایش]

اشتراک دو قرص دایره به عدسی^[ع] یا اهلیلجی موسوم است.^[۸۵] اگر دو دایره شعاع برابر داشته باشند عدسی متقارن و در غیر این‌صورت عدسی نامتقارن (یا کلی) پدید می‌آید. مساحت عدسی متقارن با شعاع ${\displaystyle R}$ و طول کمان ${\displaystyle \theta }$ رادیان عبارت است از:

${\displaystyle A=R^{2}\left(\theta -\sin \theta \right)}$

با جدا کردن عدسی از هر یک از دو دایره هلال ایجاد می‌شود. در کل از تقاطع دو دایرهٔ غیرمماس، یک عدسی و دو هلال پدید می‌آید. هلال بقراط، هلالی حاصل از برخورد دو دایره است به‌گونه‌ای که قطر دایرهٔ کوچکتر وتر و شعاع‌های متعامد دایرهٔ بزرگتر اضلاع یک مثلث متساوی‌الساقین قائم‌الزاویه باشند. می‌توان نشان داد که مساحت هلال بقراط با مساحت مثلث مذکور برابر است.

از اشتراک سه قرص دایره با شعاع مساوی که مرکز هر کدام در نقطهٔ تقاطع دو تای دیگری قرار گرفته باشد مثلث رولو حاصل می‌شود. مثلث رولو حداقل مساحت برای عرض معین در میان منحنی‌هایی با عرض ثابت را دارد. مساحت مثلث رولو ساخته‌شده از دوایری با شعاع ${\displaystyle r}$ عبات است از:^[۸۶]

${\displaystyle A={\tfrac {1}{2}}(\pi -{\sqrt {3}})r^{2}}$

مثلث رولو می‌تواند در داخل یک مربع بچرخد.^[۸۷]

برخی از قضایای دایره[ویرایش]

	قضیهٔ تالس: زاویهٔ محاطی متناظر به نیم‌دایره همواره ۹۰° است.[۸۸]
	در هر دایره، قطر عمود بر هر وتر، آن وتر و کمان‌های نظیرِ آن وتر را نصف می‌کند.[۸۹]
	در یک دایره، از دو وتر نابرابر، آنکه بزرگتر است، به مرکز دایره نزدیکتر است، و بالعکس. شکل دیگر: در یک دایره، وترهای مساوی از مرکز دایره به یک فاصله‌اند.[۹۰]
	عمودمنصف هر وتر دایره از مرکز دایره می‌گذرد.[۹۱]
	قضیه وتر: در یک دایره، حاصلضرب پاره‌خط‌های روی هر وتر حاصل از تقاطع با یک وتر دیگر برابر با حاصلضرب پاره‌خط‌های حاصل‌شده روی وتر دومی است، یعنی ${\displaystyle |AS|\cdot |SC|=|BS|\cdot |SD|=r^{2}-d^{2}}$.[۹۲]
	اگر دو خط سکانت متقاطع رسم شوند، اندازهٔ زاویه بین آن دو ${\displaystyle (\angle {A})}$ برابر است با نصف تفاضل کمان‌های محاط‌شده (${\displaystyle DE}$ و ${\displaystyle BC}$)، یعنی ${\displaystyle 2\times \angle {CAB}=\angle {DOE}-\angle {BOC}}$.
	قضیه پنج دایره: هرگاه پنج دایره که مرکزهایشان بر روی محیط دایرهٔ ششمی جای گرفته‌است، یکدیگر را زنجیروار بر روی همان دایره قطع کنند، آنگاه نقطه دوم تقاطع دایره‌ها رئوس داخلی ستاره‌ای پنج‌پرند که رئوس خارجی‌اش بر روی محیط این دایره‌ها جای گرفته‌است.[۹۳]
	زوایای روبرو در هر چهارضلعی محاطی مکملند (مجموعشان برابر ۱۸۰° است).[۹۴]
	قضیه بطلمیوس: مجموع حاصلضرب اضلاع روبروی هر چهارضلعی محاطی برابر است با حاصلضرب قطرهای آن؛ یعنی:[۹۵] ${\displaystyle |{\overline {AC}}|\cdot |{\overline {BD}}|=|{\overline {AB}}|\cdot |{\overline {CD}}|+|{\overline {BC}}|\cdot |{\overline {AD}}|}$

دستگاه دوایر[ویرایش]

مراکز و دوایر تشابه[ویرایش]

نقاط تقاطع مماس‌های مشترک دو دایره به «مراکز تشابه» آن دو دایره موسومند.^[۹۶] مرکز تشابهی که از برخورد مماس‌های مستقیم (خط‌هایی که هر دو دایره را در یک سمت لمس می‌کنند) ایجاد می‌شود «مرکز تشابه بیرونی» و مرکز تشابهی که از برخورد مماس‌های اریب (خط‌هایی که دو دایره را در دو سمت مقابل لمس می‌کنند) «مرکز تشابه درونی» نامیده می‌شود. می‌توان ثابت کرد که مراکز تشابه دایره روی خطی قرار دارند که از مراکز دو دایره می‌گذرد و این خط و امتداد آن را به نسبت شعاع‌های دو دایره تقسیم می‌کنند.^[۹۷] همچنین دایره‌ای که مرکزش روی این خط باشد و از هر دو مرکز تشابه بگذرد (قطر آن برابر فاصلهٔ بین دو مرکز تشابه باشد) به «دایرهٔ تشابه» موسوم است. می‌توان ثابت کرد که این دایره مکان هندسی همهٔ مراکز تشابه داخلی و خارجی ممکن است.^[۹۸]

در دستگاه سه زاویه‌ای شش مرکز تشابه (دو تا  ———  یکی بیرونی و یکی درونی  ———  برای هر جفت دایره) وجود دارد. می‌توان ثابت کرد که سه مرکز تشابه بیرونی روی یک خط قرار دارند و هر دو مرکز تشابه درونی با مرکز تشابه بیرونی سوم روی یک خطند.^[۹۹]

دوایر هم‌محور[ویرایش]

دستگاه دوایر به دایره‌هایی گفته می‌شود که مرکز آن‌ها روی یک خط قرار دارد و خط رادیکال (مکان هندسی نقاطی که مماس‌های ترسیم شده به هر دایره طول مساوی داشته باشند) مشترکی داشته باشند.^[۱۰۰] مجموعهٔ همهٔ دوایر هم‌محور به «مدادِ دوایر هم‌محور» موسوم است. اگر خط رادیکال یک مداد دوایر ${\displaystyle x=0}$ (برابر محور ${\displaystyle y}$ها) گرفته شود، معادلهٔ دستگاه برابر ${\displaystyle x^{2}+y^{2}+2ax\pm k^{2}=0}$ خواهد بود که ${\displaystyle k}$ مقداری ثابت است، و می‌توان نشان داد که طول مماس بر هر دایره از هر نقطه معین روی خط رادیکال ${\displaystyle ((0,h))}$ برابر ${\displaystyle h^{2}\pm k^{2}}$ و مستقل از ${\displaystyle a}$ و شعاع دایره‌ها است.^[۱۰۱]

معادله‌های دایره[ویرایش]

معادلهٔ متعارف[ویرایش]

معادلهٔ دایره‌ای که مرکزش ${\displaystyle c(h,k)}$ و شعاعش ${\displaystyle r}$ باشد عبارت است از:^[۱۰۲]

${\displaystyle (x-h)^{2}+(y-k)^{2}=r^{2}}$

و اگر مرکز دایره در مبدأ مختصاتی ${\displaystyle (h,k)=(0,0)}$ قرار بگیرد معادلهٔ آن عبارت است از:

${\displaystyle x^{2}+y^{2}=r^{2}}$

اثبات

نقطهٔ ${\displaystyle P(x,y)}$ روی دایره است اگر و تنها اگر:

${\displaystyle {\overline {PC}}=r}$

یعنی اگر و تنها اگر:

${\displaystyle {\sqrt {(x-h)^{2}+(y-k)^{2}}}=r}$

این درست است اگر و تنها اگر:

${\displaystyle (x-h)^{2}+(y-k)^{2}=r^{2}}$

معادلهٔ عام منحنی‌های درجه دو[ویرایش]

برای اینکه معادلهٔ عام منحنی‌های درجه دو (یعنی ${\displaystyle ax^{2}+2bxy+cy^{2}+2dx+2fy+g=0}$) دایره باشد، باید ${\displaystyle b}$ را برابر صفر قرار داد و ${\displaystyle a}$ را برابر ${\displaystyle c}$. با شرط ${\displaystyle a\neq 0}$ این معادله را می‌توان به شکل زیر نوشت:^[۱۰۳]

${\displaystyle a(x^{2}+y^{2})+2dx+2fy+g=0}$

که به معادلهٔ کلی دایره موسوم است. برای تبدیل این معادله به معادلهٔ متعارف دایره، می‌توان با استفاده از اتحاد مربع مجموع دو جمله‌ای عبارت بالا را به شکل زیر نوشت:^[۱۰۴]

${\displaystyle C(x,y)=(x-d)^{2}+(y-f)^{2}+k}$

که در آن ${\displaystyle k=g-d^{2}-f^{2}}$. در این معادله مرکز دایره در نقطهٔ ${\displaystyle (d,f)}$ و شعاع آن برابر با ${\displaystyle {\sqrt {-k}}}$ است. اگر ${\displaystyle k}$ کوچکتر از صفر باشد حاصل یک «دایرهٔ حقیقی»، اگر ${\displaystyle k}$ بزرگ‌تر از صفر باشد دایره حاصل یک «دایرهٔ مجازی»^[غ] و اگر ${\displaystyle k}$ برابر صفر باشد حاصل نقطه خواهد بود.^[۱۰۵]

معادلهٔ پارامتری[ویرایش]

معادلهٔ پارامتری دایره‌ای به شعاع ${\displaystyle a}$ عبارت است از:^[۱۰۶]

${\displaystyle d_{1}(t)=(a\cdot cos(t),a\cdot sin(t))}$

که در آن ${\displaystyle 0\leq t<2\pi }$.

معادلهٔ پارامتری دایره را به صورت عبارت‌های گویا نیز می‌توان نوشت. در این حالت معادلهٔ پارامتری دایره‌ای به شعاع ${\displaystyle a}$ عبارت است از:^[۱۰۷]

${\displaystyle d_{1}(t)=(a\cdot {\frac {2t}{1+t^{2}}},a\cdot {\frac {1-t^{2}}{1+t^{2}}})}$

طول کمان ${\displaystyle (s)}$، انحنا ${\displaystyle (\kappa )}$، و زاویه مماسی ${\displaystyle (\phi )}$ را نیز می‌توان به‌صورت پارامتری نوشت، که عبارتند از:^[۱۰۸]

${\displaystyle {\begin{aligned}s(t)=at\\\kappa (t)={\frac {1}{a}}\\\phi (t)={\frac {t}{a}}\end{aligned}}}$

صورت سه‌نقطه‌ای[ویرایش]

معادلهٔ دایره‌ای که از سه نقطهٔ غیر هم‌خط ${\displaystyle (x_{i},y_{i})}$ به ازای ${\displaystyle i=1,2,3}$ می‌گذرد (یعنی دایرهٔ محیطی مثلثی که رئوسش این سه نقطه‌اند) عبارت است از:^[۱۰۹]

${\displaystyle {\begin{bmatrix}x^{2}+y^{2}&x&y&1\\x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\end{bmatrix}}=0}$

این معادله را می‌توان به صورت معادلهٔ عام منحنی‌های درجه دو نوشت:

${\displaystyle ax^{2}+cy^{2}+dx+ey+f=0}$

که در آن ${\displaystyle a=c}$، مقدار ${\displaystyle b}$ صفر است (چرا که عبارتی قطری بین ${\displaystyle x}$ و ${\displaystyle y}$ در دایره نیست)، و:^[۱۱۰]

${\displaystyle {\begin{aligned}a={\begin{bmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{3}&y_{3}&1\end{bmatrix}}\\d=-{\begin{bmatrix}x_{1}^{2}+y_{1}^{2}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&y_{3}&1\end{bmatrix}}\\e={\begin{bmatrix}x_{1}^{2}+y_{1}^{2}&x_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&1\end{bmatrix}}\\f=-{\begin{bmatrix}x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}\end{bmatrix}}\end{aligned}}}$

در این‌صورت مرکز دایره در نقطهٔ ${\displaystyle (x_{0},y_{0})=(-{\tfrac {d}{2a}},-{\tfrac {e}{2a}})}$ خواهد بود و شعاع آن عبارت است از:^[۱۱۱]

${\displaystyle r={\sqrt {{\frac {d^{2}+e^{2}}{4a^{2}}}-{\frac {f}{a}}}}}$

معادله قطبی[ویرایش]

معادلهٔ قطبی دایره به محوریت مرکز آن نوشته می‌شود و شکلی ساده دارد. معادلهٔ قطبی دایره‌ای به شعاع ${\displaystyle r}$ که مرکز آن در مبدأ مختصاتی واقع شده باشد عبارت است از:^[۱۱۲]

${\displaystyle r=a}$

اگر مرکز دایره به نقطهٔ ${\displaystyle (a,0)}$ منتقل شود معادلهٔ قطبی آن عبارت خواهد بود از:^[۱۱۳]

${\displaystyle r=2a\cos {\theta }}$

و اگر مرکز دایره به نقطهٔ ${\displaystyle (0,a)}$ منتقل شود معادلهٔ قطبی آن عبارت خواهد بود از:^[۱۱۴]

${\displaystyle r=2a\sin {\theta }}$

ابرمعادله[ویرایش]

صورت عام ابرمعادله در دستگاه مختصات قطبی عبارت است از:^[۱۱۵]

${\displaystyle {\displaystyle r\left(\varphi \right)=\left(\left|{\frac {\cos \left({\frac {m_{1}\varphi }{4}}\right)}{a}}\right|^{n_{2}}+\left|{\frac {\sin \left({\frac {m_{2}\varphi }{4}}\right)}{b}}\right|^{n_{3}}\right)^{-{\frac {1}{n_{1}}}}}}$

اگر در این معادله ${\displaystyle m_{1}=m_{2}=m_{3}=2}$ باشد و ${\displaystyle n_{1}}$، ${\displaystyle n_{2}}$، و ${\displaystyle n_{3}}$ هم هر سه مساوی ۲ باشند، منحنی حاصل دایرهٔ واحد (دایره‌ای با شعاع یک) است. با ضرب کردن ${\displaystyle r}$ در معادلهٔ بالا، معادلهٔ دایره‌ای با شعاع ${\displaystyle r}$ حاصل می‌شود.^[۱۱۶]

ترسیم با خط‌کش و پرگار[ویرایش]

خط‌کش و پرگار تنها ابزارهای مجاز ترسیم در هندسه اقلیدسی هستند،^[۱۱۷] تا جایی که هندسهٔ اقلیدسی گاه «هندسهٔ خط‌کش و پرگار» خوانده شده‌است.^[۱۱۸] پرگار ابزاری برای کشیدن دایره بر اساس تعریف اقلیدسی آن است^[۱۱۹] و با خط‌کشی با طول بی‌نهایت می‌توان خط راست کشید، و هدف ریاضی‌دانان اقلیدسی این بود که همهٔ اشکال را با این دو ابزار بسازند.^[۱۲۰] بنابراین در ترسیم با خط‌کش و پرگار تنها از سه اصل اول اصول موضوعه هندسه اقلیدسی می‌توان استفاده کرد. بنابر اثبات گاوس، تنها شکل‌هایی را می‌توان با خط‌کش و پرگار رسم کرد که اندازه‌شان عدد ترسیم‌پذیر باشد. اعداد ترسیم‌پذیر اعدادی‌اند که بتوان آن‌ها را با اعمال چهار عمل اصلی و ریشه دوم بر یک عدد ترسیم‌پذیر دیگر به دست آورد (صفر و یک بنابر تعریف ترسیم‌پذیرند).

ترسیم‌های بنیادی[ویرایش]

همهٔ ترسیم‌ها با خط‌کش و پرگار با تکرار و ترکیب پنج ترسیم بنیادی در صفحه صورت می‌گیرند. این پنج ترسیم بنیادی عبارتند از:

1. ساخت یک خط با داشتن دو نقطه (اصل اول از اصول موضوعه هندسه اقلیدسی)
2. ساخت یک دایره با داشتن دو نقطه (اصل سوم از اصول موضوعه هندسه اقلیدسی)
3. ساخت یک نقطه در محل تقاطع دو خط ناموازی
4. ساخت دو نقطه در محل تقاطع یک خط و یک دایره (در صورت تقاطع)
5. ساخت دو نقطه در محل تقاطع دو دایره (در صورت تقاطع)

برخی ترسیم‌های خط‌کش و پرگار[ویرایش]

	تنصیف زاویه: برای رسم نیمساز زاویه ابتدا به مرکزیت رأس زاویه ${\displaystyle (A)}$ کمانی به شعاع دلخواه زده شود و نقاط تقاطع آن با اضلاع زاویه (${\displaystyle B}$ و ${\displaystyle C}$) مشخص شود. سپس به مرکزیت ${\displaystyle B}$ و ${\displaystyle C}$ دو کمان با شعاع مساوی و بزرگتر از نصف ${\displaystyle BC}$ زده شود. با اتصال نقاط تقاطع این کمان، نیمساز زاویه حاصل می‌شود.[۱۲۱]
	ترسیم عمودمنصف پاره‌خط: به شعاع بیش از نصف طول پاره‌خط دو کمان به مرکزیت دو سر پاره‌خط زده می‌شود. با وصل کردن نقاط تقاطع دو کمان، عمودمنصف پاره‌خط حاصل می‌شود.[۱۲۲]
	رسم عمودی بر خط از نقطه‌ای بیرون آن: به مرکزیت نقطه ${\displaystyle P}$ کمانی به شعاع دلخواه زده می‌شود تا خط را در ${\displaystyle A'}$ و ${\displaystyle B'}$ قطع کند. سپس به روش مذکور در بالا عمودمنصف پاره خط ${\displaystyle A'B'}$ ترسیم می‌شود.[۱۲۳]
	ترسیم دایره با داشتن سه نقطه غیرهم‌خط ${\displaystyle A}$، ${\displaystyle B}$، و ${\displaystyle C}$: به روش بالا عمودمنصف پاره‌خط‌های ${\displaystyle {\overline {AB}}}$ و ${\displaystyle {\overline {BC}}}$ رسم می‌شود. نقطهٔ تقاطع دو عمودمنصف مرکز دایره است و می‌توان از آن به فاصلهٔ هر کدام از نقاط دایره را رسم کرد.

ترسیم‌های غیرممکن[ویرایش]

یکی از مسائل کهن ریاضی که در طول تاریخ ریاضی‌دانان را درگیر خود کرده بود تربیع دایره است و مطلوب آن ترسیم مربعی با خط‌کش و پرگار است که مساحت آن با مساحت دایره‌ای مفروض برابر باشد. شکل دیگری از این مسئله ترسیم مربعی با خط‌کش و پرگار است که محیط آن با محیط دایرهٔ مفروض برابر باشد.^[۱۲۴] در ۱۸۸۲ فردیناند فون لیندمن نشان داد که پی عددی متعالی است، و تربیع دایره غیرممکن است. در زبان انگلیسی «تربیع دایره» (به انگلیسی: squaring the circle) وارد ادبیات شده‌است و همچنین ضرب‌المثلی به مفهوم «عمل غیرممکن» است.^[۱۲۵]

تثلیث زاویه و تضعیف مکعب (یا «مسئلهٔ دلوسی») نیز دو مسئله کهن دیگر ترسیم با خط‌کش و پرگارند که هدف اولی تقسیم زاویه به سه قسمت مساوی است و هدف دومی ترسیم مکعبی که حجم آن دو برابر حجم مکعبی مفروض (هر ضلع آن ${\displaystyle {\sqrt[{3}]{2}}}$ برابر ضلع مکعب مفروض) باشد.^[۱۲۶] ترسیم هفت‌ضلعی منتظم با استفاده از خط‌کش و پرگار (یا تقسیم دایره به هفت کمان مساوی، موسوم به تسبیع دایره هم از مسائلی است که به‌ویژه دانشمندان عصر طلایی اسلام را به خود مشغول داشته بود.^[۱۲۷] در سال ۱۷۸۶ کارل فریدریش گاوس گاوس نشان داد که هفت کوچک‌ترین عدد ترسیم‌ناپذیر است و نمی‌توان هفت‌ضلعی منتظم را با پرگار و خط‌کش ترسیم کرد.^[۱۲۸]

در بعدهای بالاتر[ویرایش]

تعمیم دایره در فضای سه‌بعدی کره نام دارد.^[۱۲۹] همهٔ نقاط روی سطح کره از مرکز آن به یک فاصله‌اند. همچنین تعمیم دایره در فضای ${\displaystyle n+1}$بعدی به ${\displaystyle n}$-کره موسوم است.^[۱۳۰] ${\displaystyle n}$-کره مجموعهٔ همهٔ نقاطی است که در فضای ${\displaystyle n+1}$بعدی از یک نقطهٔ معین فاصلهٔ یکسانی داشته باشند. به‌این‌ترتیب ۱-کره همان دایره و ۲-کره همان کره است.

همچنین حاصل اکستروژن موازی دایره استوانه و حاصل اکستروژن مرکزی آن مخروط است.

جستارهای وابسته[ویرایش]

• رئوس مطالب دایره

یادداشت‌ها[ویرایش]

منابع[ویرایش]

پانویس[ویرایش]

فهرست منابع[ویرایش]