In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative...

In mathematics, the QM-AM-GM-HM inequalities, also known as the mean inequality chain, state the relationship between the harmonic mean, geometric mean...

{\displaystyle \{\alpha ,\beta \}=\{0,1\}.} This also follows from the weighted AM-GM inequality. Theorem — Suppose a > 0 {\displaystyle a>0} and b > 0. {\displaystyle...

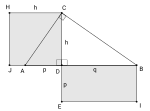
length. Another application of provides a geometrical proof of the AM–GM inequality in the case of two numbers. For the numbers p and q one constructs...

{\displaystyle 15} minutes. AM, GM, and HM satisfy these inequalities: A M ≥ G M ≥ H M {\displaystyle \mathrm {AM} \geq \mathrm {GM} \geq \mathrm {HM} \,}...

we did in the AM-HM proof. Let x = a + b , y = b + c , z = c + a {\displaystyle x=a+b,y=b+c,z=c+a} . We then apply the AM-GM inequality to obtain x +...

the three classical Pythagorean means are the arithmetic mean (AM), the geometric mean (GM), and the harmonic mean (HM). These means were studied with proportions...

This is implied, via the AM–GM inequality, by a stronger inequality which has also been called the isoperimetric inequality for triangles: T ≤ 3 4 ( a...

text processor such as Microsoft Word. Fréchet mean Generalized mean Inequality of arithmetic and geometric means Sample mean and covariance Standard...

Proof without words of the AM–GM inequality: PR is the diameter of a circle centered on O; its radius AO is the arithmetic mean of a and b. Using the geometric...